A liquid of refractive index 1.5 is poured into a cyclindrical jar of radius 20 cm upto a height of 20 cm. A small bulb at the centre of bottom glowing. Find area of the liquid surface through which the light of the bulb passes into air.
To solve the problem step by step, we will follow these steps:
Step 1: Understand the Problem
We have a cylindrical jar with a radius of 20 cm filled with a liquid of refractive index 1.5 up to a height of 20 cm. A bulb is placed at the center of the bottom of the jar, and we need to find the area of the liquid surface through which the light from the bulb can pass into the air.
Step 2: Identify the Critical Angle
The critical angle (c) can be found using the formula:
sinc=1μ
where μ is the refractive index of the liquid. Given that μ=1.5:
sinc=11.5=23
Step 3: Calculate the Critical Angle
Using the inverse sine function, we can find the critical angle:
c=sin−1(23)
Step 4: Calculate the Tangent of the Critical Angle
We can also find the tangent of the critical angle using the relationship:
tanc=1√μ2−1
Substituting μ=1.5:
tanc=1√(1.5)2−1=1√2.25−1=1√1.25=1√5/4=2√5
Step 5: Relate the Radius of the Area to the Height
Using the relationship between the radius (r) of the area through which light can escape and the height (h) of the liquid:
rh=tanc
Given h=20 cm=0.2 m:
r=h⋅tanc=0.2⋅2√5=0.4√5 m
Step 6: Calculate the Area of the Liquid Surface
The area (A) through which light passes into the air can be calculated using the formula for the area of a circle:
A=πr2
Substituting the value of r:
A=π(0.4√5)2=π⋅0.165=0.16π5 m2
Calculating this gives:
A≈0.16⋅3.145≈0.1005 m2
Final Answer
The area of the liquid surface through which the light of the bulb passes into the air is approximately:
0.1 m2
We have a cylindrical jar with a radius of 20 cm filled with a liquid of refractive index 1.5 up to a height of 20 cm. A bulb is placed at the center of the bottom of the jar, and we need to find the area of the liquid surface through which the light from the bulb can pass into the air.
The critical angle (c) can be found using the formula:
sinc=1μ
where μ is the refractive index of the liquid. Given that μ=1.5:
sinc=11.5=23
Using the inverse sine function, we can find the critical angle:
c=sin−1(23)
We can also find the tangent of the critical angle using the relationship:
tanc=1√μ2−1
Substituting μ=1.5:
tanc=1√(1.5)2−1=1√2.25−1=1√1.25=1√5/4=2√5
Using the relationship between the radius (r) of the area through which light can escape and the height (h) of the liquid:
rh=tanc
Given h=20 cm=0.2 m:
r=h⋅tanc=0.2⋅2√5=0.4√5 m
The area (A) through which light passes into the air can be calculated using the formula for the area of a circle:
A=πr2
Substituting the value of r:
A=π(0.4√5)2=π⋅0.165=0.16π5 m2
Calculating this gives:
A≈0.16⋅3.145≈0.1005 m2
The area of the liquid surface through which the light of the bulb passes into the air is approximately:
0.1 m2
Similar Questions
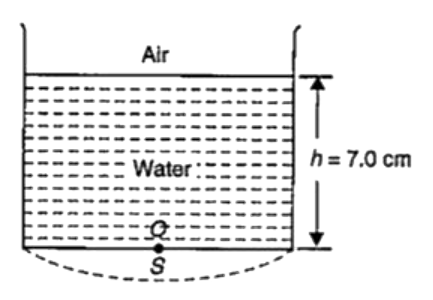
A point source of monochromatic light .S. is kept at the centre Cof the bottom of a cylinder, Radius of circular base of the cylinder is 15.0 cm. The cylinder contains water (refractive index =43 ) to a height of 7.0 cm (see figure)
Find the area of water surface through which light emerges in air.
 View Solution
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View Solution
Knowledge Check
- Question 1 - Select One
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
A2.6m2B3.6m2C4.2m2D5.8m2
A biconvex lens made of glass (refractive index 1.5) has two spherical surfaces having radii 20cm and 30cm. Calculate its focal length.
View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA liquid of refractive index 1.6 is contained in the cavity of a glass specimen of refractive index 1.5 as shown in figure. If each of the curve surface has a radius of curvature of 0.20m, the arrangement obehaves as a
 View Solution
View SolutionA small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from the bulb can emerge. Take the value of refractive index of water to be 4/3.
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View SolutionA denser medium of refractive index 1.5 has a concave surface of radius of curvature 12 cm. An object is situated in the denser medium at a distance of 9 cm from the pole. Locate the image due to refraction in air.
View Solution

