A ray of light incident on the horizontal surface of a glass slab at 70∘ just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
To solve the problem, we need to find the critical angle and the refractive index of the glass slab when a ray of light is incident at an angle of 70∘ and just grazes the adjacent vertical surface after refraction.
1. Understanding the Geometry:
- We have a glass slab with a horizontal surface. The ray of light is incident at an angle of 70∘ to the normal at the horizontal surface.
- After refraction, the ray grazes the adjacent vertical surface, which means it undergoes total internal reflection at the vertical surface.
2. Using Snell's Law:
- According to Snell's Law, n1sinθ1=n2sinθ2, where:
- n1 is the refractive index of air (approximately 1),
- θ1 is the angle of incidence (70∘),
- n2 is the refractive index of glass (μ),
- θ2 is the angle of refraction.
- Since the ray grazes the vertical surface, it means that the angle of refraction (θ2) is equal to the critical angle (c).
3. Setting Up the Equation:
- From Snell's Law, we can write:
1⋅sin(70∘)=μ⋅sin(c)
- Rearranging gives:
μ=sin(70∘)sin(c)
4. Relating Critical Angle and Refraction:
- For total internal reflection to occur, we have the relationship:
sin(c)=1μ
- This means that we can substitute sin(c) in our previous equation:
μ=sin(70∘)1/μ
- This simplifies to:
μ2=sin(70∘)
5. Calculating the Refractive Index:
- Now, we can find μ:
μ=√sin(70∘)
- Using a calculator, we find sin(70∘)≈0.9397:
μ≈√0.9397≈0.969
6. Finding the Critical Angle:
- Now, we can find the critical angle using:
c=sin−1(1μ)
- Substituting the value of μ:
c=sin−1(10.969)
- Calculating this gives:
c≈46∘
Final Results:
- The critical angle c is approximately 46∘.
- The refractive index μ of the glass is approximately 1.37.
- We have a glass slab with a horizontal surface. The ray of light is incident at an angle of 70∘ to the normal at the horizontal surface.
- After refraction, the ray grazes the adjacent vertical surface, which means it undergoes total internal reflection at the vertical surface.
- According to Snell's Law, n1sinθ1=n2sinθ2, where:
- n1 is the refractive index of air (approximately 1),
- θ1 is the angle of incidence (70∘),
- n2 is the refractive index of glass (μ),
- θ2 is the angle of refraction.
- From Snell's Law, we can write:
1⋅sin(70∘)=μ⋅sin(c)
- Rearranging gives:
μ=sin(70∘)sin(c)
- For total internal reflection to occur, we have the relationship:
sin(c)=1μ
- This means that we can substitute sin(c) in our previous equation:
μ=sin(70∘)1/μ
- This simplifies to:
μ2=sin(70∘)
- Now, we can find μ:
μ=√sin(70∘)
- Using a calculator, we find sin(70∘)≈0.9397:
μ≈√0.9397≈0.969
- Now, we can find the critical angle using:
c=sin−1(1μ)
- Substituting the value of μ:
c=sin−1(10.969)
- Calculating this gives:
c≈46∘
- The critical angle c is approximately 46∘.
- The refractive index μ of the glass is approximately 1.37.
Similar Questions
Ordinary light is incident on the upper surface of a glass slab at theh polarizing angle. Then
View SolutionFind the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC. (Refractive index of glass =1.6.)
View SolutionUnpolarized light is incident on a plane surface of glass of refractive index μ at angle i. If the reflected light gets totally polarized, write the relation between the angle i and refractive index μ.
View SolutionFind the angle of incidence at which a ray of monochromatic light should be incident on the first surface AB of a regular glass prism ABC so that the emergent ray grazes the adjacent surface AC.(Refractive Index of glass = 1.56)
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionA ray of light is incident on a surface of glass slab at an angle 45∘. If the lateral shift produced per unit thickness is 1/√3, the angle of refraction produced is
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
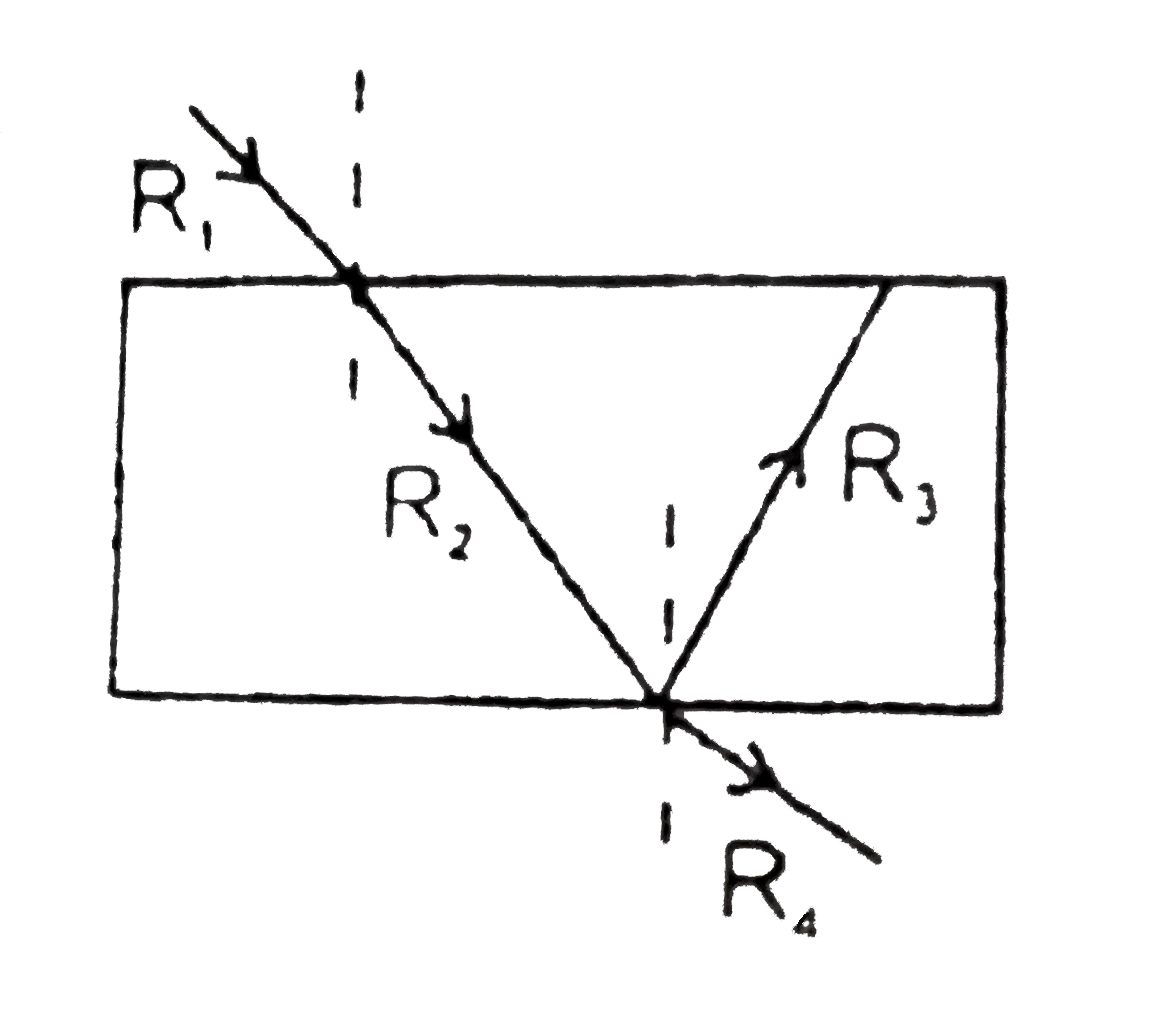 View Solution
View SolutionA ray R1 is incident on the plane surface of the glass slab (kept in air) of refractive index √2 at angle of incident equal to the critical angle for this air glass system. The refracted ray R2 undergoes partial reflection & refraction at the other surface. The angle between the reflected ray R3 and the refracted ray R4 at that surface is :
 View Solution
View SolutionA ray LM of monochromatic light incident normally on one refracting surface AB of a regular glass prism ABC emerges in air from the adjacent surface C as shown in figure. Calculate the refractive index of the material of the prism.
View Solution

