A ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index The radius of the sphere is R. At t = 0, the ball is dropped to fall normally on the sphere. Find the speed of the image formed as a function of time for t<√2hg. Consider only the image by a single refraction.
To solve the problem of finding the speed of the image formed by a ball dropped from a height h above a transparent sphere of radius R and refractive index μ, we can follow these steps:
Step 1: Determine the height of the ball above the sphere as a function of time
The ball is dropped from a height h and falls under the influence of gravity. The distance fallen after time t is given by:
h′=12gt2
Thus, the remaining height of the ball above the surface of the sphere at time t is:
habove=h−h′=h−12gt2
Step 2: Apply the refraction formula
To find the position of the image formed by the refraction at the spherical surface, we can use the lens maker's formula for refraction at a spherical surface:
μ2v−μ1u=μ2−μ1R
Where:
- μ2=μ (refractive index of the sphere)
- μ1=1 (refractive index of air)
- u=−habove (object distance, negative because the object is above the surface)
- v is the image distance we want to find.
Substituting these values into the equation gives:
μv−1−(h−12gt2)=μ−1R
Step 3: Rearranging the equation
Rearranging the equation to solve for v:
μv+1h−12gt2=μ−1R
This can be rewritten as:
μv=μ−1R−1h−12gt2
Taking the reciprocal gives:
v=μR(h−12gt2)(μ−1)(h−12gt2)−R
Step 4: Differentiate to find the speed of the image
To find the speed of the image, we differentiate v with respect to time t:
dvdt=ddt⎛⎝μR(h−12gt2)(μ−1)(h−12gt2)−R⎞⎠
Using the quotient rule:
dvdt=(denominator)⋅(derivative of the numerator)−(numerator)⋅(derivative of the denominator)(denominator)2
This will yield the speed of the image as a function of time.
Final Expression
After performing the differentiation and simplifying, we will arrive at the expression for the speed of the image as a function of time.
The ball is dropped from a height h and falls under the influence of gravity. The distance fallen after time t is given by:
h′=12gt2
Thus, the remaining height of the ball above the surface of the sphere at time t is:
habove=h−h′=h−12gt2
To find the position of the image formed by the refraction at the spherical surface, we can use the lens maker's formula for refraction at a spherical surface:
μ2v−μ1u=μ2−μ1R
Where:
- μ2=μ (refractive index of the sphere)
- μ1=1 (refractive index of air)
- u=−habove (object distance, negative because the object is above the surface)
- v is the image distance we want to find.
μv−1−(h−12gt2)=μ−1R
Rearranging the equation to solve for v:
μv+1h−12gt2=μ−1R
This can be rewritten as:
μv=μ−1R−1h−12gt2
Taking the reciprocal gives:
v=μR(h−12gt2)(μ−1)(h−12gt2)−R
To find the speed of the image, we differentiate v with respect to time t:
dvdt=ddt⎛⎝μR(h−12gt2)(μ−1)(h−12gt2)−R⎞⎠
Using the quotient rule:
dvdt=(denominator)⋅(derivative of the numerator)−(numerator)⋅(derivative of the denominator)(denominator)2
This will yield the speed of the image as a function of time.
After performing the differentiation and simplifying, we will arrive at the expression for the speed of the image as a function of time.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXAMPLE
75 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assignment (Section - I) Subjective Type Questions
6 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
Does the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View Solution
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
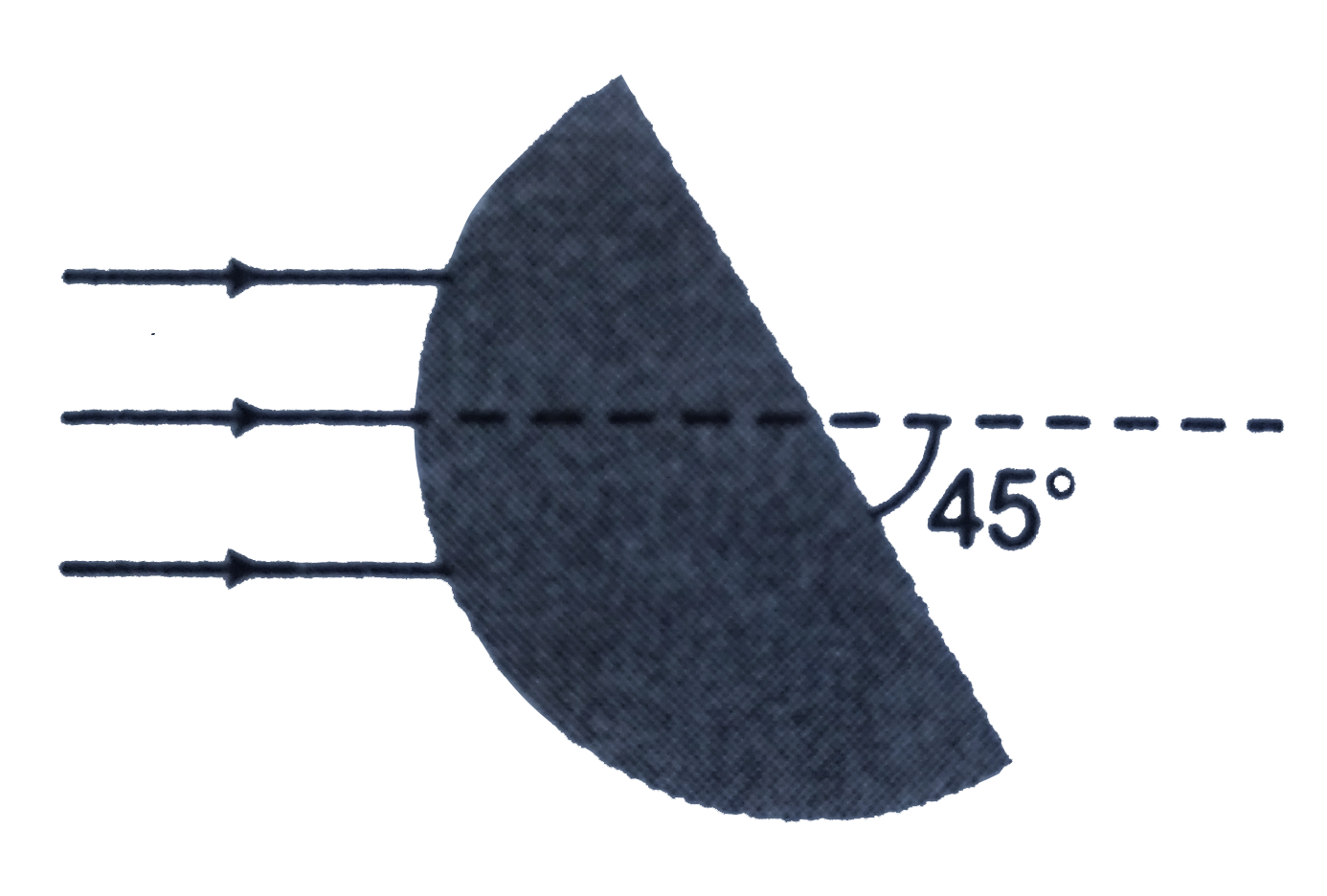
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
View SolutionA sphere made of transparent material of refractive index (μ=32 )and of radius 50 cm has a small air bubble 10 cm below the surface. The apparent depth of the bubble if viewed from outside normally is
View SolutionA lead sphere is dropped into a medium. As the sphere falls, the velocity of lead sphere
View SolutionFigure shows a transparent hemisphere of radius 3.0 cm made of a material of refractive index 2.0. (a) A narrow beam of parallel rays is incident on the hemisphere as shown in the figure. Are the rays totally reflected at the plane surface ? (b) Find the image formed by the refraction at the first surface. (c) Find the image formed by the reflection or by the refraction at the plane surface. (d) Trace qualitatively the final rays as they come out of the hemisphere.

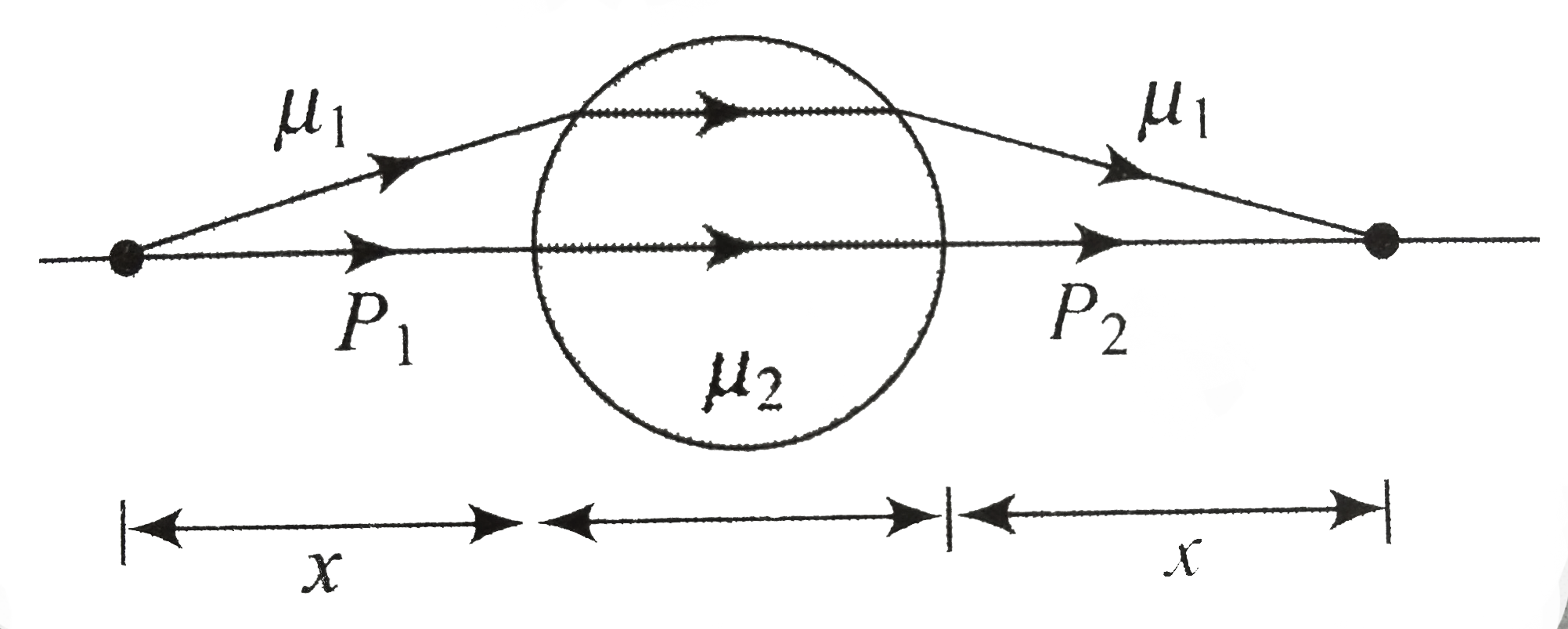
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View Solution
