A sphere made of transparent material of refractive index (μ=32 )and of radius 50 cm has a small air bubble 10 cm below the surface. The apparent depth of the bubble if viewed from outside normally is
-507 cm
257cm
1007 cm
757cm
The correct Answer is:A
To find the apparent depth of the air bubble located 10 cm below the surface of a transparent sphere with a refractive index of μ=32, we can use the formula for apparent depth in a medium. The formula we will use is:
μ2v−μ1u=μ2−μ1r
Where:
- μ1 is the refractive index of the sphere (which is 32 or 1.5),
- μ2 is the refractive index of air (which is 1),
- u is the actual depth of the bubble (which is -10 cm, negative because it is below the surface),
- v is the apparent depth we want to find,
- r is the radius of the sphere (which is -50 cm, negative because it is measured from the surface downwards).
Step 1: Substitute the known values into the formula
Substituting the values into the formula, we have:
1v−1.5−10=1−1.5−50
Step 2: Simplify the equation
This simplifies to:
1v+1.510=−0.5−50
Step 3: Calculate the right-hand side
Calculating the right-hand side:
−0.5−50=0.550=0.01
Step 4: Substitute back into the equation
Now we can rewrite the equation:
1v+0.15=0.01
Step 5: Isolate 1v
To isolate 1v:
1v=0.01−0.15
Calculating this gives:
1v=−0.14
Step 6: Solve for v
Now, we can find v:
v=1−0.14≈−7.14 cm
Conclusion
Thus, the apparent depth of the bubble when viewed from outside normally is approximately 7.14 cm below the surface of the sphere.
- μ1 is the refractive index of the sphere (which is 32 or 1.5),
- μ2 is the refractive index of air (which is 1),
- u is the actual depth of the bubble (which is -10 cm, negative because it is below the surface),
- v is the apparent depth we want to find,
- r is the radius of the sphere (which is -50 cm, negative because it is measured from the surface downwards).
Topper's Solved these Questions
Similar Questions
Does the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?
View SolutionA ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index The radius of the sphere is R. At t = 0, the ball is dropped to fall normally on the sphere. Find the speed of the image formed as a function of time for t<√2hg. Consider only the image by a single refraction.
View SolutionA glass sphere (μ=1.5) of radius 20 cm has a small air bubble 4 cm below its centre. The sphere is viewed from outside and along a vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
View Solution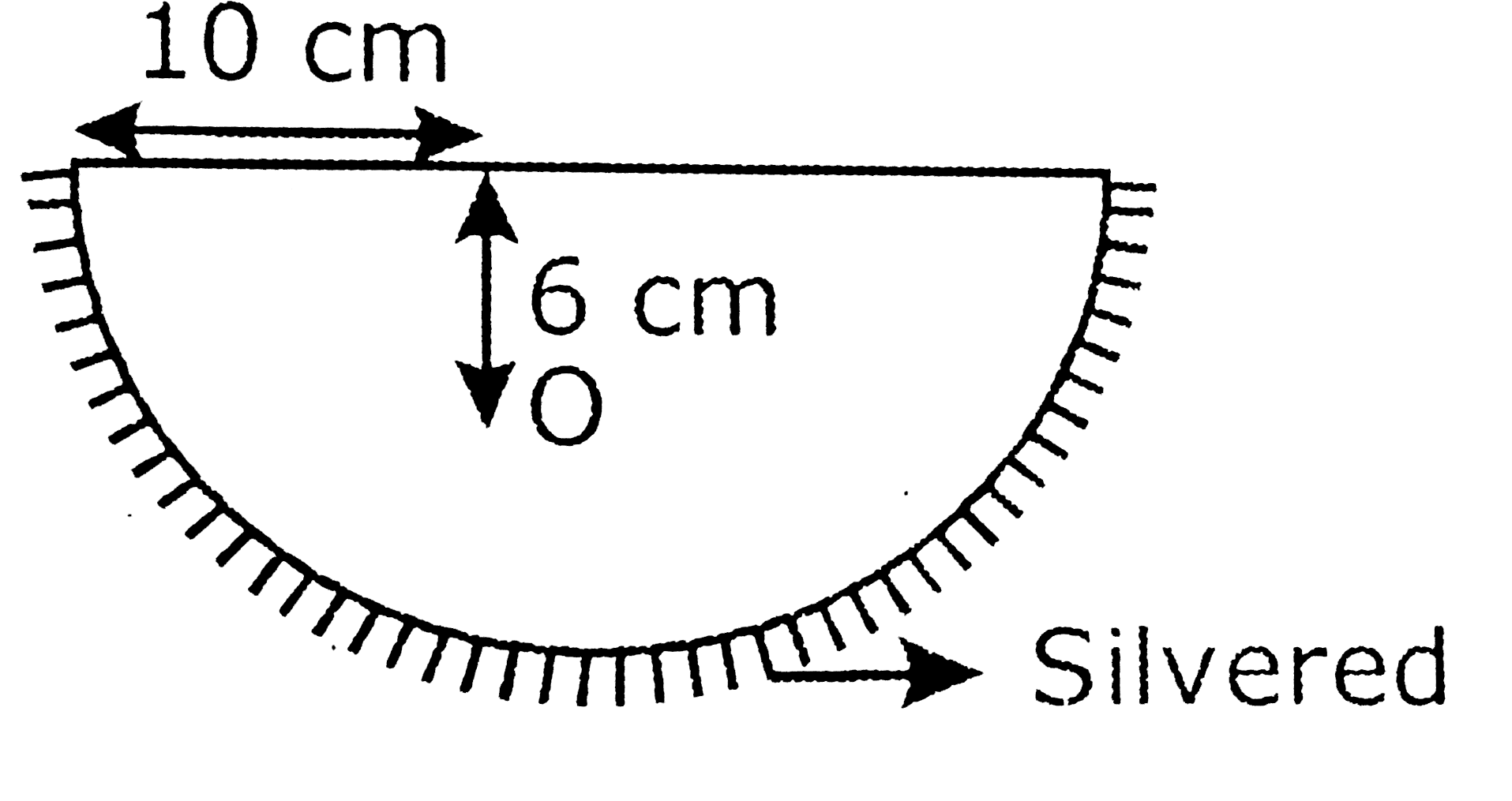
A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface . A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.

View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.

View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.

View SolutionA glass sphere of diameter 50 cm and μ=1.5 has a small air bubble. Looking from outside the diameter, the bubble appears to be at a distance 10 cm the surface. Find the apparent position of the bubble when it is viewed from the diametrically opposite position.
View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionTwo immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air
View Solution
