A nucleus X232 initially at rest undergoes α decay, the α-particle produced in above process is found to move in a circular track of radius 0.22 m in a uniform magnetic field of 1.5 T. Find Q value of reaction.
The correct Answer is:5.5 MeV
To find the Q value of the reaction for the alpha decay of the nucleus X232, we can follow these steps:
Step 1: Understand the Problem
The nucleus X232 undergoes alpha decay, producing an alpha particle and a residual nucleus. The alpha particle moves in a circular path in a magnetic field, and we are given the radius of this path and the strength of the magnetic field.
Step 2: Use the Formula for Radius in a Magnetic Field
The radius R of the circular path of a charged particle in a magnetic field is given by the formula:
R=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
Step 3: Rearranging the Formula
We can rearrange this formula to find the kinetic energy E of the alpha particle:
E=12mv2
From R=mvqB, we can express v as:
v=qBRm
Substituting this into the kinetic energy formula gives:
E=12m(qBRm)2=q2B2R22m
Step 4: Calculate the Charge and Mass of the Alpha Particle
The charge q of an alpha particle (which consists of 2 protons) is:
q=2e=2×1.6×10−19C=3.2×10−19C
The mass m of an alpha particle is approximately:
m=4u=4×1.66×10−27kg≈6.64×10−27kg
Step 5: Substitute Values into the Energy Equation
Substituting the known values into the energy equation:
- R=0.22m
- B=1.5T
We get:
E=(3.2×10−19)2×(1.5)2×(0.22)22×(6.64×10−27)
Step 6: Calculate the Energy
Calculating the above expression step-by-step:
1. Calculate (3.2×10−19)2=1.024×10−37
2. Calculate (1.5)2=2.25
3. Calculate (0.22)2=0.0484
4. Combine these:
E=1.024×10−37×2.25×0.04842×6.64×10−27
Step 7: Find Q Value
The Q value of the reaction can be calculated from the energy of the alpha particle and the mass difference before and after the decay. The Q value is given by:
Q=E+(massofX232−massofresidualnucleus−massofalphaparticle)×c2
Final Calculation
After calculating the energy E and considering the mass difference, we can find the Q value.
The nucleus X232 undergoes alpha decay, producing an alpha particle and a residual nucleus. The alpha particle moves in a circular path in a magnetic field, and we are given the radius of this path and the strength of the magnetic field.
The radius R of the circular path of a charged particle in a magnetic field is given by the formula:
R=mvqB
where:
- m is the mass of the particle,
- v is the velocity of the particle,
- q is the charge of the particle,
- B is the magnetic field strength.
We can rearrange this formula to find the kinetic energy E of the alpha particle:
E=12mv2
From R=mvqB, we can express v as:
v=qBRm
Substituting this into the kinetic energy formula gives:
E=12m(qBRm)2=q2B2R22m
The charge q of an alpha particle (which consists of 2 protons) is:
q=2e=2×1.6×10−19C=3.2×10−19C
The mass m of an alpha particle is approximately:
m=4u=4×1.66×10−27kg≈6.64×10−27kg
Substituting the known values into the energy equation:
- R=0.22m
- B=1.5T
E=(3.2×10−19)2×(1.5)2×(0.22)22×(6.64×10−27)
Calculating the above expression step-by-step:
1. Calculate (3.2×10−19)2=1.024×10−37
2. Calculate (1.5)2=2.25
3. Calculate (0.22)2=0.0484
4. Combine these:
E=1.024×10−37×2.25×0.04842×6.64×10−27
The Q value of the reaction can be calculated from the energy of the alpha particle and the mass difference before and after the decay. The Q value is given by:
Q=E+(massofX232−massofresidualnucleus−massofalphaparticle)×c2
After calculating the energy E and considering the mass difference, we can find the Q value.
Topper's Solved these Questions
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - Assignment Section J (Aakash Challengers Questions)
3 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - EXERCISE
20 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - Assignment Section H (Multiple True-False)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)
13 Videos
Similar Questions
A nucleus X of mass M. intially at rest undergoes alpha decay according to the equation
_(Z)AX→.A−4Z−2Y+.42He
The alpha particle emitted in the above proces is found to move in a circular track of radius r in a uniform magnetic field B. Then (mass and charge of α particle are m and q respectively)
View SolutionThe momentum of α-particles moving in a circular path of radius 10 cm in a perpendicular magnetic field of 0.05 tesla will be :
View SolutionA proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionA nucleus X, initially at rest, undergoes alpha-decay according to the equation.
_92AX→228ZY+α
(a) Find the values of A and Z in the above process.
(b) The alpha particle produced in the above process is found in move in a circular track of during the process and the binding energy of the parent nucleus X.
Given that m(Y)=228.03u, m(_0^1n)=1.009u<br>m(_24He)=4.003u, m(_1^1H)=1.008u
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
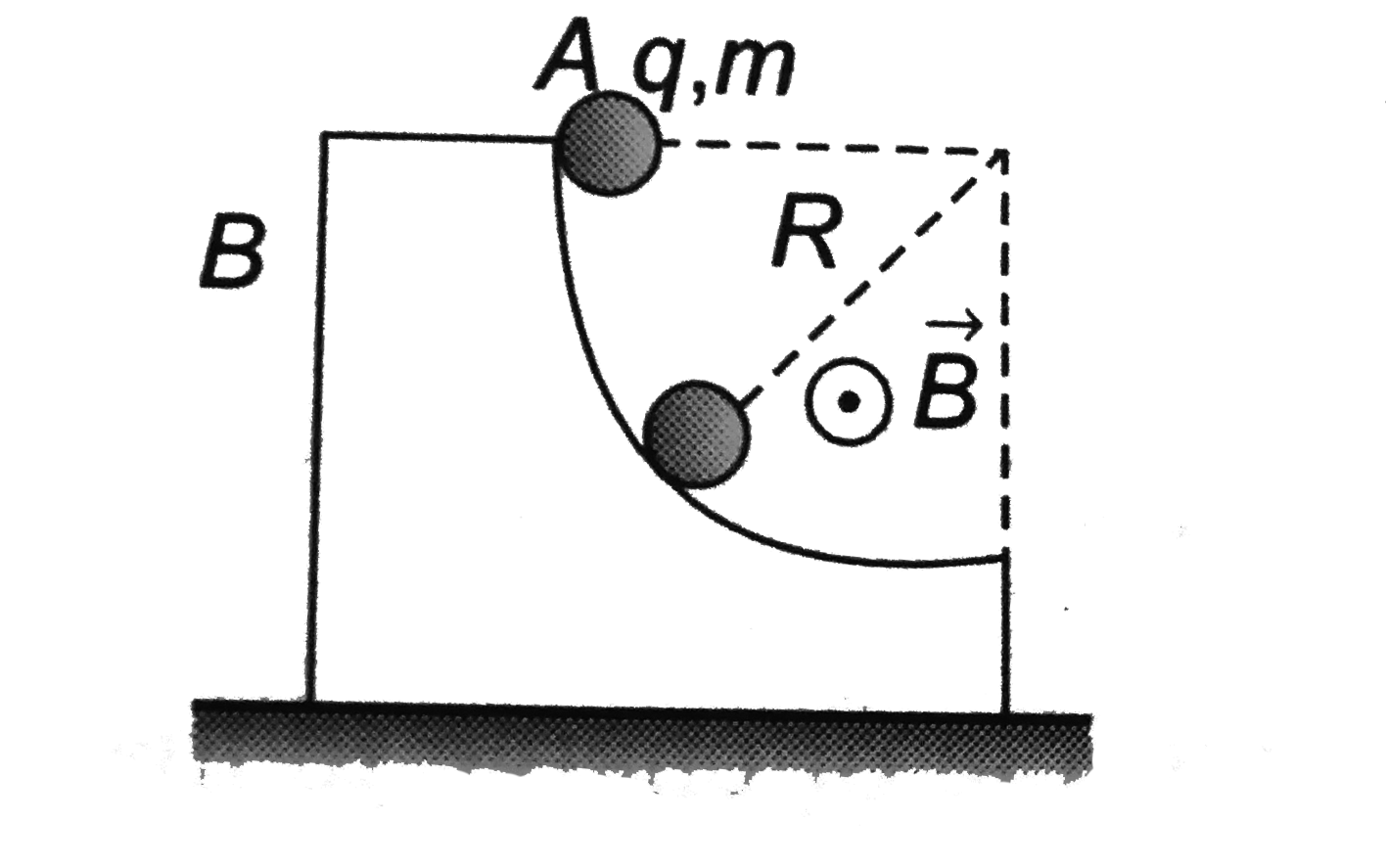
View SolutionIn the figure a charged small sphere of mass m and the charge q starts sliding from rest on a vertical fixed circular smooth track of radius R from the position A shown. There exist a uniform magnetic field of B. Find the maximum force exerted by track on the sphere during its motion.
View SolutionA current - carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of (6.0×10−5) T at its centre. Find the value of the current.
View SolutionSuppose a nucleus initally at rest undergoes α decay according to equation
.22592X→Y+α
At t=0, the emitted α-particles enter a region of space where a uniform magnetic field →B=B0ˆi and elecrtic field →E=E0ˆi exist. The α-particles enters in the region with velocity →V=v0ˆj from x=0. At timet=√3×106m0q0E0s, the particle was observed to have speed twice the initial velocity v0. Then, find (a) the velocity v0 of the α-particles,
(b) the initial velocity v0 of the α-particle, (c ) the binding energy per nucleon of the α-particle.
[Given thatm(Y)=221.03u,m(α)=4.003u,m(n)=1.09u,m(P)=1.008u].
View SolutionSuppose a nucleus initally at rest undergoes α decay according to equation
.23592X→Y+α
At t=0, the emitted α-partilces enter a region of space where a uniform magnetic field →B=B0ˆj and elcertis field →E=E0ˆi exist. The α-prticles enters in the region with velocity →V=v0ˆj from x=0. At timet=√3×106m0q0E0s, the particle was observed to have speed twice the initial velocity v0. Then, find (a) the velocity v0 of the α-particles,
(b) the initial velocity v0 of the α-particle, (c ) the binding energy per nucleon of the α-particle.
[Given thatm(Y)=221.03u,m(α)=4.003u,m(n)=1.09u,m(P)=1.008u].
View Solution
