A dimensionless quantity y is represented by the formula . Which of following is/arecorrect?
Dimensions of d and e are same
abc and de have same dimensions
is dimensionless
de+dc is not meaningful
The correct Answer is:1,2,4
To solve the problem, we need to analyze the given expression for the dimensionless quantity y:
y=a−bcd+e
Since y is dimensionless, we can conclude that the dimensions of the numerator must equal the dimensions of the denominator. This leads us to the following steps:
Step 1: Understand the implications of y being dimensionless
Since y is dimensionless, we have:
(a−bc)=(d+e)
This means that the dimensions of a and bc must be the same as the dimensions of d and e.
Step 2: Analyze the terms
1. Dimensions of a: Let the dimension of a be (A).
2. Dimensions of b: Let the dimension of b be (B).
3. Dimensions of c: Let the dimension of c be (C).
4. Dimensions of d: Let the dimension of d be (D).
5. Dimensions of e: Let the dimension of e be (E).
From the equation (a−bc)=(d+e), we can deduce:
- Since bc is a product, its dimension is (B)(C).
- Therefore, we have (A)=(B)(C) and (D)=(E).
Step 3: Evaluate the options
1. Option 1: Dimensions of d and e are the same.
- Since we have (D)=(E), this statement is correct.
2. Option 2: a,b,c, and d have the same dimensions.
- We have (A)=(B)(C) and (D)=(E). There is no direct relationship that states all four have the same dimensions. Thus, this statement is incorrect.
3. Option 3: bca+d is dimensionless.
- Since (bc)=(B)(C) and (a+d) has dimensions (A) (which is not equal to (B)(C)), this statement is incorrect.
4. Option 4: d+bc is not meaningful.
- Since (D) (dimension of d) is not the same as (B)(C) (dimension of bc), we cannot add these two terms. Thus, this statement is correct.
Conclusion
From the analysis, we find:
- Option 1: Correct
- Option 2: Incorrect
- Option 3: Incorrect
- Option 4: Correct
Final Answer
The correct options are 1 and 4.
---
Since y is dimensionless, we have:
1. Dimensions of a: Let the dimension of a be (A).
2. Dimensions of b: Let the dimension of b be (B).
3. Dimensions of c: Let the dimension of c be (C).
4. Dimensions of d: Let the dimension of d be (D).
5. Dimensions of e: Let the dimension of e be (E).
- Therefore, we have (A)=(B)(C) and (D)=(E).
1. Option 1: Dimensions of d and e are the same.
- Since we have (D)=(E), this statement is correct.
- We have (A)=(B)(C) and (D)=(E). There is no direct relationship that states all four have the same dimensions. Thus, this statement is incorrect.
- Since (bc)=(B)(C) and (a+d) has dimensions (A) (which is not equal to (B)(C)), this statement is incorrect.
- Since (D) (dimension of d) is not the same as (B)(C) (dimension of bc), we cannot add these two terms. Thus, this statement is correct.
From the analysis, we find:
- Option 1: Correct
- Option 2: Incorrect
- Option 3: Incorrect
- Option 4: Correct
The correct options are 1 and 4.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION D (Linked Comprehension)
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION E (Assertion-Reason)
11 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION B Objective (One option is correct )
45 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
Knowledge Check
Which of the following is dimensionless?
AForce/accelerationBVelocity/accelerationCVolume/areaDEnergy/workNaHCO3 represents the formula of which one of the following?
ASodium carbonateBWashing sodaCSodium acetateDBaking soda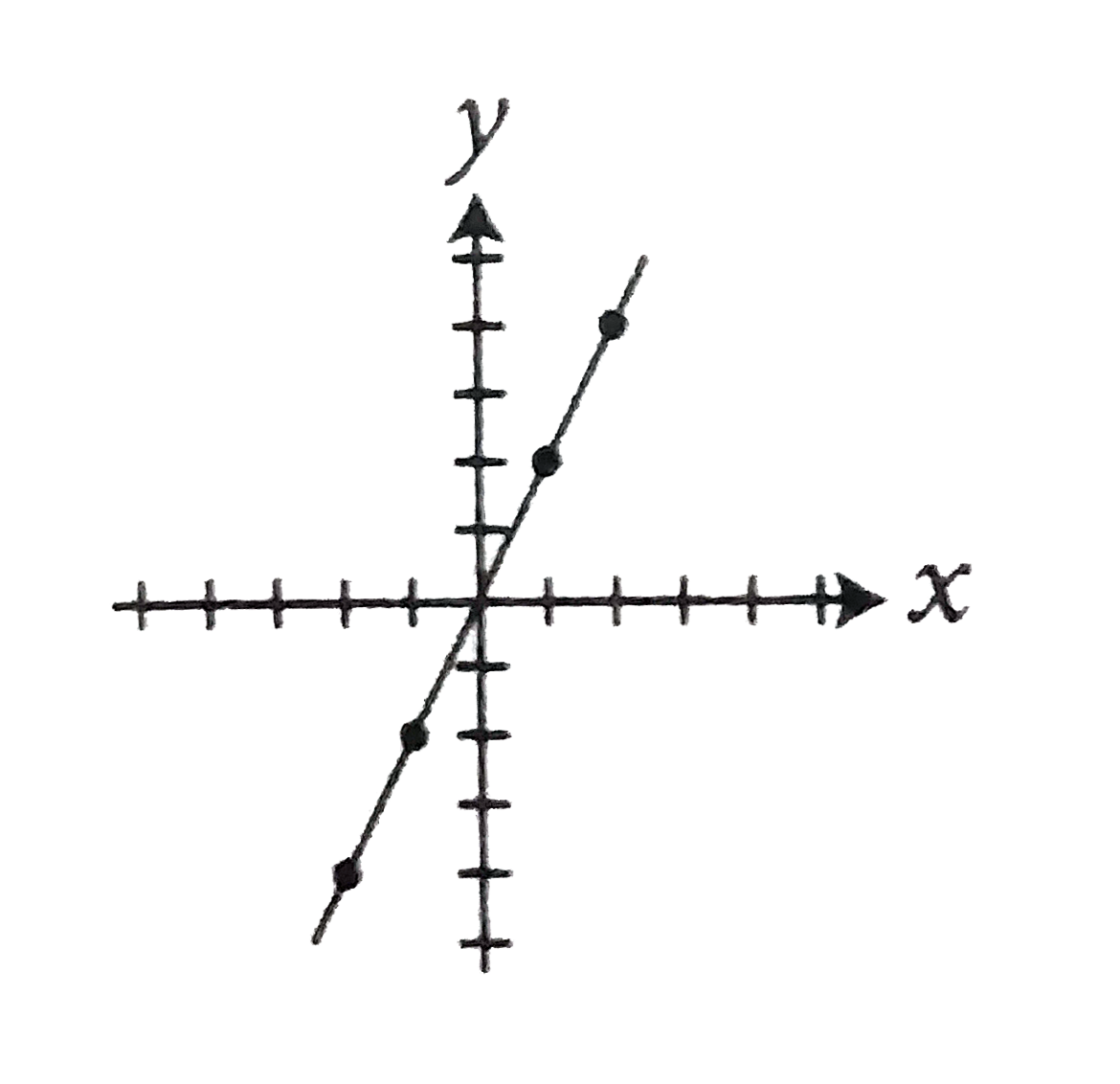
The graph above shows y=2x. Which of the following graphs represents y=|2x|?A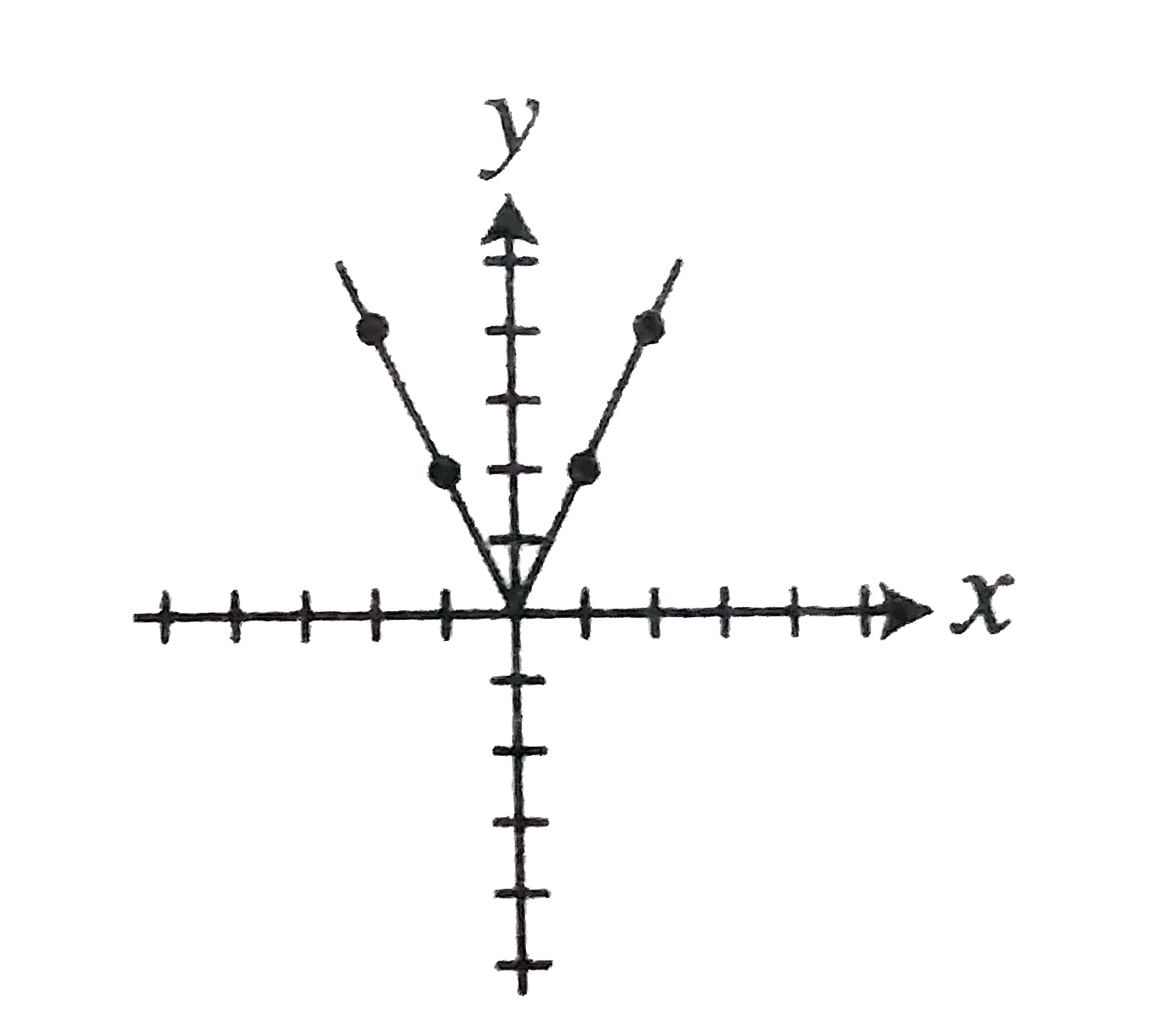 B
B C
C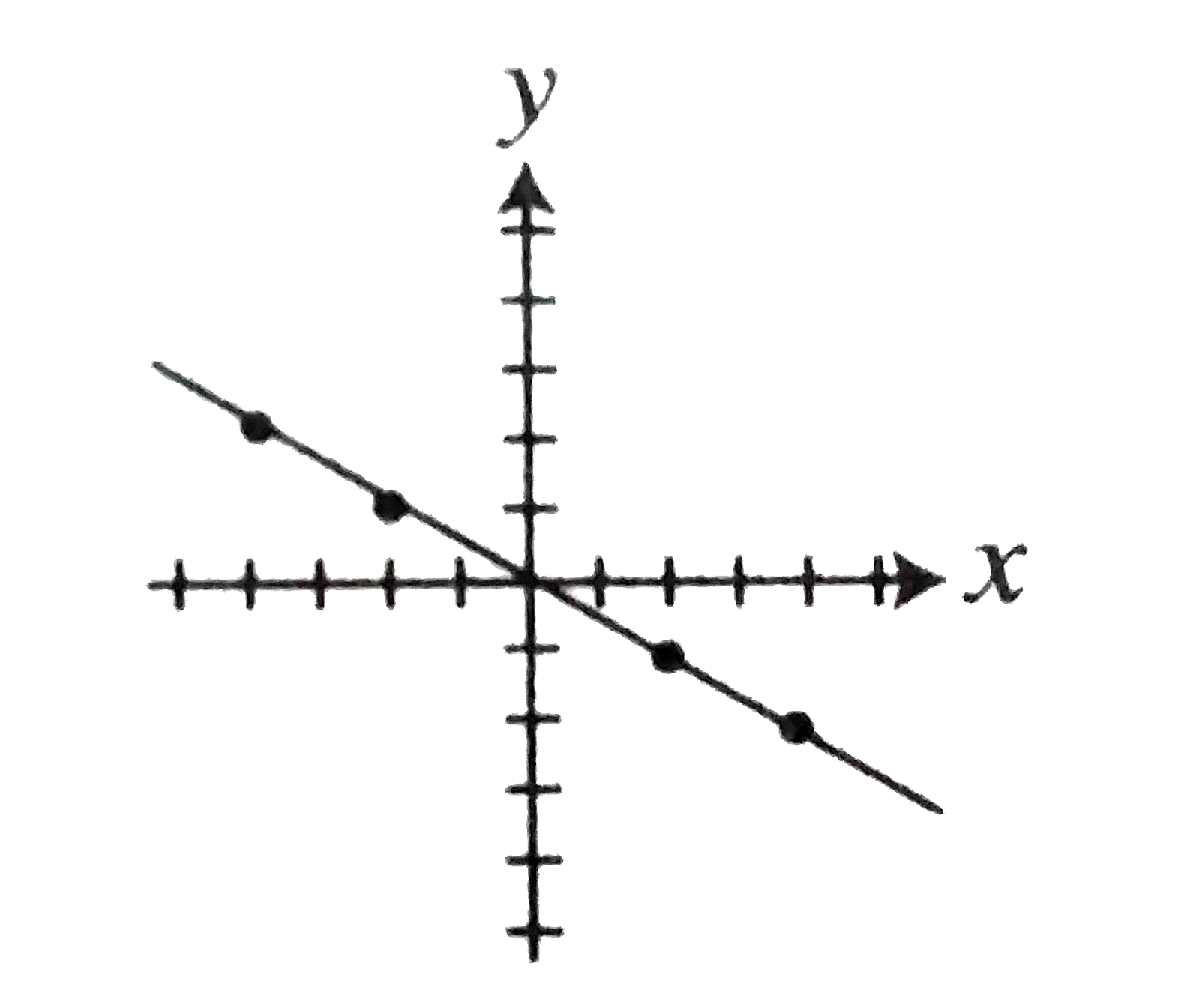 D
D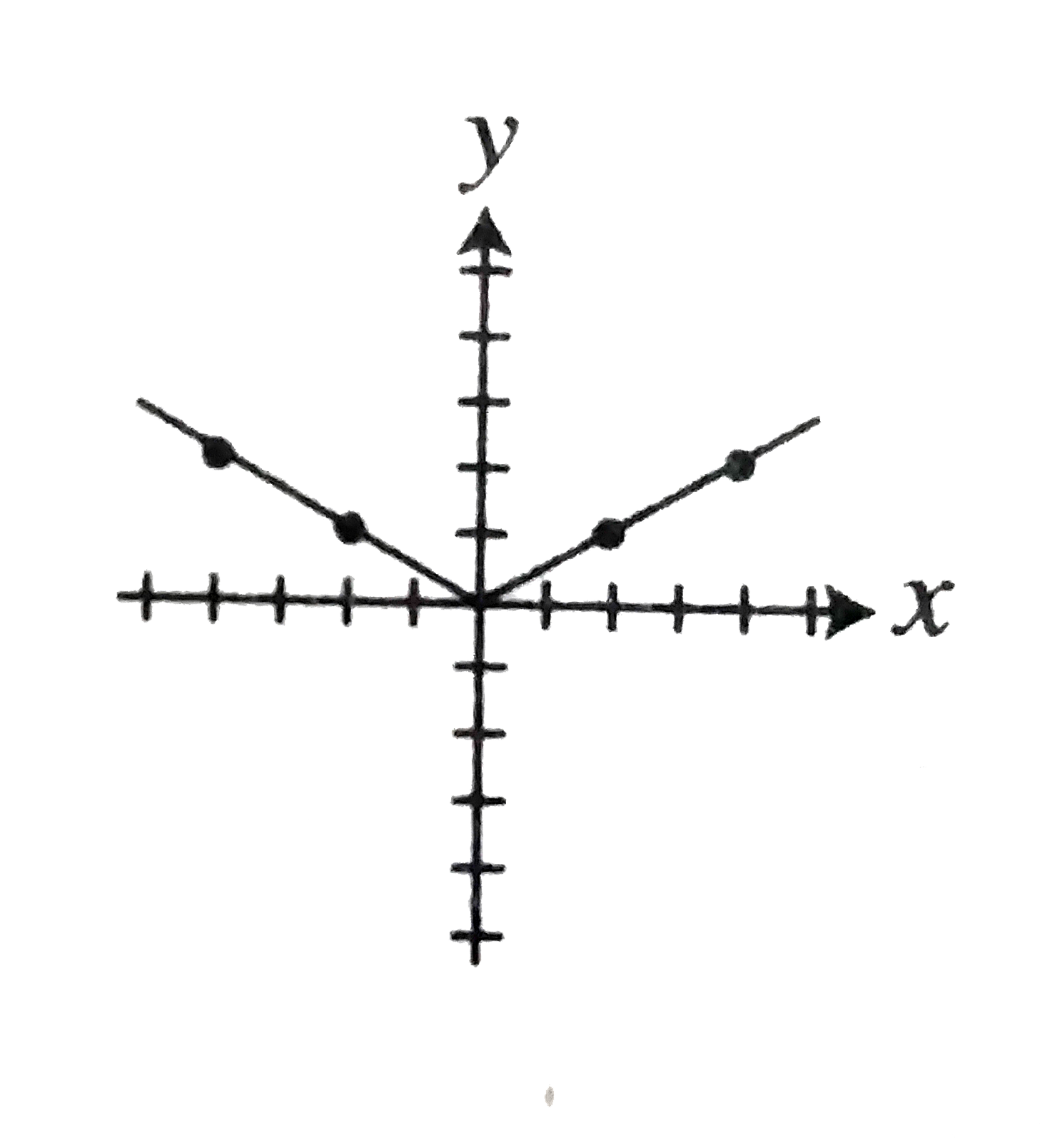
Which of the following represents an E isomer?
View SolutionIf velocity, force and time are taken as the fundamental quantities, them using dimensional analysis choose the correct dimensional formula for mass among the following. [K is a dimensionless constant]
View SolutionWhich of the following represents a correct chemical formula? Name it.
View SolutionLet y=Asin(ωt−kx) represent the variation of distance y of a particle with time t. Which of the following is not meaningful?
View SolutionWhich of the following formulae represent an alkane?
View Solution

