The radius of a spherical ball is (10.4 ± 0.4) cm Select the correct alternative
The percentage error in radius is 3.9%
The percentage error in radius is 0.4%
The percentage error in volume is 11. 5%
The absolute error in volume is 1.2 cm
The correct Answer is:1,3
To solve the problem, we need to find the percentage error in the radius and the volume of the spherical ball given its radius and the associated error.
Step 1: Identify the given values
- Radius of the spherical ball, R=10.4cm
- Absolute error in radius, ΔR=0.4cm
Step 2: Calculate the percentage error in radius
The formula for percentage error is given by:
Percentage Error=(ΔRR)×100
Substituting the values:
Percentage Error in Radius=(0.410.4)×100
Calculating this:
Percentage Error in Radius=(0.03846)×100≈3.85%
Step 3: Calculate the volume of the sphere
The volume V of a sphere is given by the formula:
V=43πR3
Substituting R=10.4cm:
V=43π(10.4)3
Calculating (10.4)3:
(10.4)3=1121.664cm3
Now substituting back to find V:
V≈43π(1121.664)≈4690.56cm3
Step 4: Calculate the percentage error in volume
The volume is related to the radius cubed, so the percentage error in volume can be calculated using the formula:
ΔVV=3ΔRR
Thus, the percentage error in volume is:
Percentage Error in Volume=3(ΔRR)×100
Substituting the values:
Percentage Error in Volume=3(0.410.4)×100
Calculating this:
Percentage Error in Volume=3×3.85%≈11.54%
Step 5: Check the options
Now, we can check the options provided in the question:
1. The % error in radius is 9.4% - False
2. The % error in radius is 0.4% - False
3. The % error in volume is 11.5% - False
4. The absolute error in volume is 1.2 cm - False
Final Result
- Percentage error in radius: 3.85%
- Percentage error in volume: 11.54%
- Radius of the spherical ball, R=10.4cm
- Absolute error in radius, ΔR=0.4cm
The formula for percentage error is given by:
The volume V of a sphere is given by the formula:
The volume is related to the radius cubed, so the percentage error in volume can be calculated using the formula:
Now, we can check the options provided in the question:
1. The % error in radius is 9.4% - False
2. The % error in radius is 0.4% - False
3. The % error in volume is 11.5% - False
4. The absolute error in volume is 1.2 cm - False
- Percentage error in radius: 3.85%
- Percentage error in volume: 11.54%
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION D (Linked Comprehension)
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION E (Assertion-Reason)
11 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION B Objective (One option is correct )
45 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
Select the correct alternative(s)
View SolutionSelect the correct alternative(s).
View SolutionSelect the correct alternative(s).
View SolutionSelect the correct alternative (s)
View SolutionThe radius of a spherical ball of iron is 1.5 cm. It is melted and recast into three spherical balls. If the radii of two such balls are 0.75 cm and 1 cm, then find the radius of 3rd ball.
View SolutionThe radius of a sphericla ball of iron is 1.5 cm .It is melted and recast into three sperical balls .If the radii of two such balls are 0.75 cm and 1 cm , then find the radius of 3rd ball .
View SolutionAcceleration of a particle which is at rest at x=0 is →a=(4−2x)ˆi. Select the correct alternative (s).
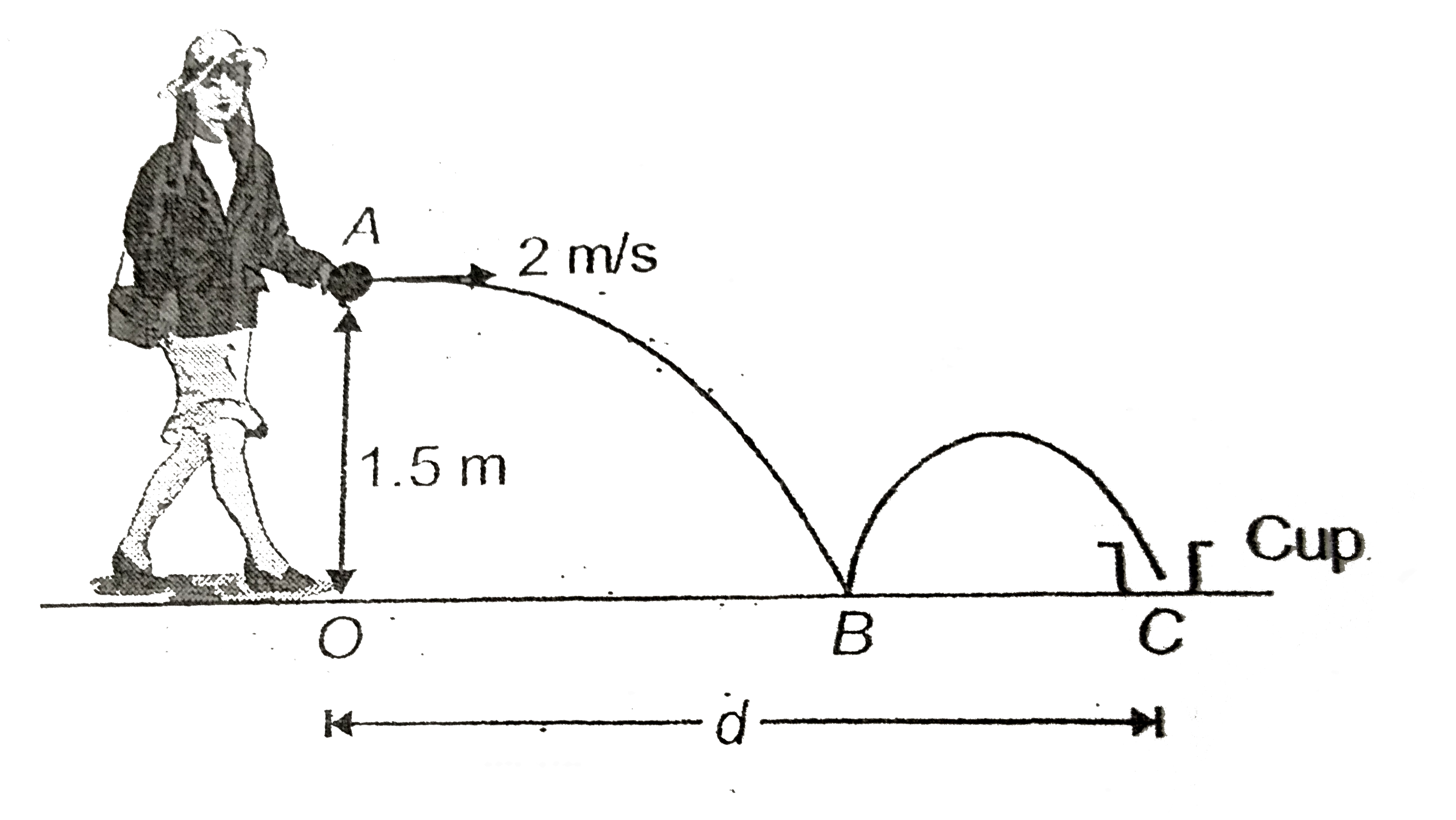
View SolutionA girl throws the ball with horizontal velocity 2m/s at the moment t=0. The ball bounces once on the smooth floor and then lands into cup C. The coefficient of restitution for the collision is 0.8. Select the correct alternative (g=10m/s2)
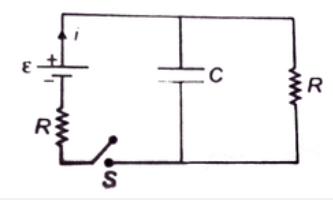
View SolutionIn the circuit shown, the switch is closed at t=0. Select the correct alternative(s)
View SolutionThe radius of a ball is (5.2±0.2) cm. The percentage error in the volume of the ball is (approximately).
View Solution
