The number of divisions of 9600 , including 1 and 9600 are
50
48
58
46
The correct Answer is:B
To find the number of divisors of the number 9600, we will follow these steps:
Step 1: Prime Factorization of 9600
We start by performing the prime factorization of 9600. We can divide 9600 by 2 (the smallest prime number) repeatedly until we can no longer divide evenly by 2:
- 9600÷2=4800
- 4800÷2=2400
- 2400÷2=1200
- 1200÷2=600
- 600÷2=300
- 300÷2=150
- 150÷2=75
Now, we can no longer divide by 2. Next, we try dividing by the next smallest prime number, which is 3:
- 75÷3=25
Finally, we divide by 5:
- 25÷5=5
- 5÷5=1
Thus, the prime factorization of 9600 is:
9600=27×31×52
Step 2: Using the Divisor Formula
To find the number of divisors of a number based on its prime factorization, we use the formula:
If n=pe11×pe22×…×pekk, then the number of divisors d(n)=(e1+1)(e2+1)…(ek+1)
In our case:
- For 27, e1=7
- For 31, e2=1
- For 52, e3=2
Now we apply the formula:
d(9600)=(7+1)(1+1)(2+1)
Step 3: Calculate the Number of Divisors
Now, we calculate each term:
- 7+1=8
- 1+1=2
- 2+1=3
Now multiply these results together:
d(9600)=8×2×3
Calculating this gives:
d(9600)=48
Conclusion
Thus, the total number of divisors of 9600, including 1 and 9600 itself, is 48.
---
We start by performing the prime factorization of 9600. We can divide 9600 by 2 (the smallest prime number) repeatedly until we can no longer divide evenly by 2:
- 4800÷2=2400
- 2400÷2=1200
- 1200÷2=600
- 600÷2=300
- 300÷2=150
- 150÷2=75
- 5÷5=1
9600=27×31×52
To find the number of divisors of a number based on its prime factorization, we use the formula:
If n=pe11×pe22×…×pekk, then the number of divisors d(n)=(e1+1)(e2+1)…(ek+1)
- For 27, e1=7
- For 31, e2=1
- For 52, e3=2
d(9600)=(7+1)(1+1)(2+1)
Now, we calculate each term:
- 7+1=8
- 1+1=2
- 2+1=3
d(9600)=8×2×3
d(9600)=48
Thus, the total number of divisors of 9600, including 1 and 9600 itself, is 48.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS Book:AAKASH INSTITUTE ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:Assignment Section C Objective type questions (One option is correct )
Explore 17 Videos
- PERMUTATIONS AND COMBINATIONS Book:AAKASH INSTITUTE ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:Assignment Section D Linked Comprehension Type Questions
Explore 12 Videos
- PERMUTATIONS AND COMBINATIONS Book:AAKASH INSTITUTE ENGLISHChapter:PERMUTATIONS AND COMBINATIONS Exercise:Assignment Section A Objective type questions (One option is correct )
Explore 51 Videos
- MATRICESBook:AAKASH INSTITUTE ENGLISHChapter:MATRICESExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 3 Videos
- PRINCIPLE OF MATHEMATICAL Book:AAKASH INSTITUTE ENGLISHChapter:PRINCIPLE OF MATHEMATICAL Exercise:Section-D:(Assertion-Reason Type Questions)
Explore 11 Videos
Similar Questions
The sum of the divisors of 9600 is
View SolutionNumber of even divisions of 504 is
View SolutionThe number 24! is divisible by
View SolutionThe figure shows the variation of energy with the orbit radius of a body in circular planetary motion.
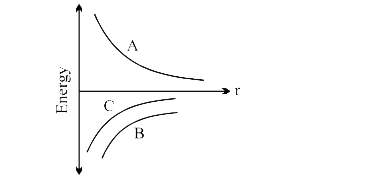
Find the correct statement about the curves A, B and C
View SolutionThe least count of a veriner callipers is 1100cm. The value of one division on the main scale is 1mm. The, the number of divisions on the main scale that coincide with N divisions of the vernier is
View SolutionFor N=50400 the number of divisor of N, which are divisible by 6, divisible by
View SolutionThe number of cervial vertebrae in mammals including human beings are
View SolutionLet X and Y be the sets of all positive divisions of400 and 1000 respectively (including 1 and the number). Then n(X∩Y) is T, then T4 is-
View SolutionThe toal number of isomers including stereoisomers for 1,3-
dimethyl cyclohexane is:
View SolutionThe total number of isomer including stereosisomers for 1,2-dimethyl cyclobutane is:
View Solution