The equation of common tangents to the ellipse x2+2y2=1 and the circle x2+y2=23 is
y=√7√2+√3
y=7x+√3
y=√7x+√2
none of these
To find the equation of the common tangents to the ellipse x2+2y2=1 and the circle x2+y2=23, we will follow these steps:
Step 1: Write the equations in standard form
The equation of the ellipse can be rewritten in standard form:
x21+y212=1
This shows that a2=1 and b2=12.
The equation of the circle is already in standard form:
x2+y2=23
This indicates that the center of the circle is at (0, 0) and the radius r=√23.
Step 2: Write the equation of the tangent to the ellipse
The equation of the tangent to the ellipse in terms of slope m is given by:
y=mx±√a2m2+b2
Substituting a2=1 and b2=12, we get:
y=mx±√m2+12
Step 3: Find the distance from the center of the circle to the tangent line
The distance d from the center of the circle (0, 0) to the tangent line y=mx+c is given by:
d=|c|√1+m2
Here, c=±√m2+12.
Step 4: Set the distance equal to the radius of the circle
We equate the distance to the radius of the circle:
√m2+12√1+m2=√23
Step 5: Square both sides to eliminate the square root
Squaring both sides gives:
m2+121+m2=23
Step 6: Cross-multiply to solve for m2
Cross-multiplying yields:
3(m2+12)=2(1+m2)
Expanding this gives:
3m2+32=2+2m2
Rearranging leads to:
m2=2−32=12
Step 7: Find the values of m
Thus, we find:
m=±1√2
Step 8: Substitute m back into the tangent equation
Substituting m back into the tangent equation:
y=±1√2x±√12+12=±1√2x±1
Final Step: Write the equations of the common tangents
The equations of the common tangents are:
y=1√2x+1,y=1√2x−1,y=−1√2x+1,y=−1√2x−1
The equation of the ellipse can be rewritten in standard form:
x21+y212=1
This shows that a2=1 and b2=12.
x2+y2=23
This indicates that the center of the circle is at (0, 0) and the radius r=√23.
The equation of the tangent to the ellipse in terms of slope m is given by:
y=mx±√a2m2+b2
Substituting a2=1 and b2=12, we get:
y=mx±√m2+12
The distance d from the center of the circle (0, 0) to the tangent line y=mx+c is given by:
d=|c|√1+m2
Here, c=±√m2+12.
We equate the distance to the radius of the circle:
√m2+12√1+m2=√23
Squaring both sides gives:
m2+121+m2=23
Cross-multiplying yields:
3(m2+12)=2(1+m2)
Expanding this gives:
3m2+32=2+2m2
Rearranging leads to:
m2=2−32=12
Thus, we find:
m=±1√2
Substituting m back into the tangent equation:
y=±1√2x±√12+12=±1√2x±1
The equations of the common tangents are:
y=1√2x+1,y=1√2x−1,y=−1√2x+1,y=−1√2x−1
Similar Questions
The number of common tangents to the ellipse x216+y29=1 and the circle x2+y2=4 is
View SolutionIf L be the length of common tangent to the ellipse x225+y24=1 and the circle x2+y2=16 intercepted by the coordinates axis then √3L2 is _____
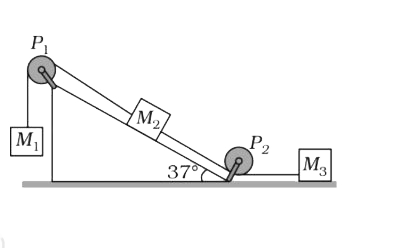
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionThe equation of common tangent of the curve x2+4y2=8 and y2=4x are
View SolutionEquation of a common tangent to the circle x2+y2−6x=0 and the parabola y2=4x is
View SolutionThe slopes of the common tangents of the ellipse x24+y21=1 and the circle x2+y2=3 are ±1 (b) ±√2 (c) ±√3 (d) none of these
View SolutionThe minimum length of intercept on any tangent to the ellipse x24+y29=1 cut by the circle x2+y2=25 is :
View SolutionThe equation of the tangents to the circle x2+y2=25 with slope 2 is
View SolutionThe product of the slopes of the common tangents of the ellipse x2+4y2=16 and the parabola y2−4x−4=0 is
View SolutionThe equation of the common tangent to the parabolas y2=2xandx2=16y is
View Solution
