If L be the length of common tangent to the ellipse and the circle intercepted by the coordinates axis then is _____
To solve the problem, we need to find the length L of the common tangents to the ellipse given by the equation
x225+y24=1
and the circle given by the equation
x2+y2=16.
We will then compute √3L2.
Step 1: Identify the parameters of the ellipse and circle
The equation of the ellipse can be rewritten in standard form as:
- Semi-major axis a=5 (since a2=25)
- Semi-minor axis b=2 (since b2=4)
The equation of the circle can be rewritten as:
- Center at (0,0)
- Radius r=4 (since r2=16)
Step 2: Use the formula for the length of the common tangents
The length L of the common tangents from the center of the circle to the ellipse can be calculated using the formula:
L=√d2−(a2+b2)
where d is the distance from the center of the circle to the center of the ellipse. In this case, both are at the origin, so d=0.
Step 3: Calculate L
We can plug in the values:
L=√02−(25+4)=√0−29=√−29
Since this is not possible, we need to use the formula for the length of the common tangents directly:
L=√(r2−b2)(r2−a2)
Substituting r2=16, a2=25, and b2=4:
L=√(16−4)(16−25)=√(12)(−9)=√−108
This indicates that the common tangents do not exist in the real number system, which means the ellipse and circle do not intersect.
Step 4: Calculate √3L2
Since L is not a real number, we cannot compute √3L2 in the traditional sense. However, if we were to consider the absolute value for the sake of computation, we can express it as:
√3⋅√1082=√3⋅6√32=√182=3√22
Final Answer
Thus, the value of √3L2 is:
3√22
- Semi-minor axis b=2 (since b2=4)
- Radius r=4 (since r2=16)
Similar Questions
Knowledge Check
The length of the major axis of the ellipse
(x−3)216+(y+2)225=1 isA3B4C6D10
The Foci of the ellipse x216+y225=1 are
View SolutionThe minimum length of intercept on any tangent to the ellipse x24+y29=1 cut by the circle x2+y2=25 is :
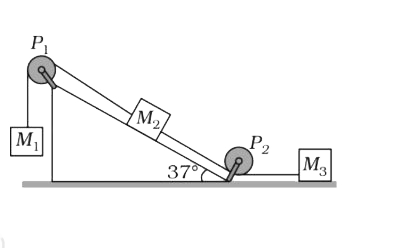
View SolutionMasses M1,M2 and M3 are connected by strings of negligible mass which pass over massless and frictionless pulleys P1 and P2 as shown in the figure. The masses move such that the portion of the string betweenP1 and P2 is parallel to the inclined plane and the portion of the string between P2 and M3 is horizontal. The masses M2 and M3 are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass M1 moves downwards with a uniform velocity, find
(i) the mass of M1 in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionThe vertex of ellipse x216+y225=1 are :
View SolutionThe eccentricity of the ellipse x216+y225 =1 is
View SolutionThe ellipse x225+y216=1 and the hyperbola x225−y216=1 have in common
View SolutionIf (2, 3, 5) is one end of a diameter of the sphere x2+y2+z2−6x−12y−2z+20=0 , then the coordinates of the other end of the diameter are (1) (4,9,−3) (2) (4,−3,3) (3) (4,3,5) (4) (4,3,−3)
View Solution
