The set of the counting numbers which are multiple of 6 and less than 50 is written in set builder form as

A

{ x : x ∈ N and x is a multiple of 6 }

B

{ x : x = 6 and 0 < x < 50 }

C

{ x : x is a multiple of 6 and 0 < x < 50 , x ∈ N }

D

{ x : x is a multiple of 6 and x ≤ 50 }

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:C

To express the set of counting numbers that are multiples of 6 and less than 50 in set builder form, follow these steps:

1. Identify the Elements: We need to find counting numbers that are multiples of 6. Counting numbers start from 1 and go upwards (1, 2, 3, ...).

2. Define the Condition: The numbers must be multiples of 6. A number x is a multiple of 6 if it can be expressed as x=6n, where n is a positive integer.

3. Set the Range: The problem states that these multiples of 6 should be less than 50. Therefore, we need to ensure that x<50.

4. Combine the Conditions: We can express the conditions as:
- x is a multiple of 6 (i.e., x=6n for some integer n)
- x<50
- Since we are dealing with counting numbers, we also need x>0.

5. Write in Set Builder Notation: Combining these conditions, we can write the set in set builder form as:
{x∈N:x=6n,n∈N,x<50}

Final Answer:
The set of counting numbers which are multiples of 6 and less than 50 in set builder form is:
{x∈N:x=6n,n∈N,x<50}

Updated on:7/8/2024
|
Class 12MATHSSETS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If ocr_image is the solution set of a linear in equation in x, then the solution set of x in set-builder form is:

    A{x:−4≤x≤2,x∈R}
    B{x:−5<x<3,x∈R}
    C{x:−4≤x≤2,x∈N}
    D{x:−5<x<3,x∈I}

  • The following diagram represents the solution of two sets P and Q on the number line:
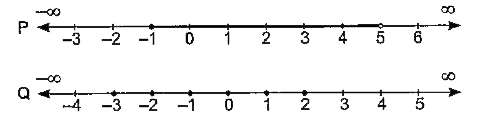
    ocr_image
    The solution set of Q in set builder form is:

    A{x:−3<x<2,x∈R}
    B{x:−3≤x≤2,x∈I}
    C{x:−3<x≤2,x∈N}
    D{x:−3≤x<2,x∈W}