In a series LCR circuit, voltage applied is V=3sin(314t+π6) and current from the supply is l=2sin(315t+π3). Which of the following is correct ?
Impendance of circuit is 1.5Ω
Reactance of circuit is 43Ω
Resistance of circuit is 3√34Ω
Wattless component of current is 1√2
The correct Answer is:A, C, D
To solve the problem, we need to analyze the given voltage and current equations in the LCR circuit and determine which statements about the circuit are correct.
Given:
- Voltage: V=3sin(314t+π6)
- Current: I=2sin(315t+π3)
Step 1: Identify the parameters from the voltage and current equations.
From the voltage equation:
- Amplitude of voltage, V0=3
- Angular frequency of voltage, ωv=314
- Phase angle of voltage, ϕv=π6
From the current equation:
- Amplitude of current, I0=2
- Angular frequency of current, ωi=315
- Phase angle of current, ϕi=π3
Step 2: Calculate the impedance of the circuit.
In a series LCR circuit, the impedance Z can be calculated using the formula:
Z=V0I0
Substituting the values we have:
Z=32=1.5ohm
Step 3: Determine the reactance of the circuit.
The reactance X in a series LCR circuit can be calculated using:
XL=ωLandXC=1ωC
However, we do not have the values of L and C provided in the problem, so we cannot calculate the reactance directly. Thus, we cannot confirm the reactance statement.
Step 4: Calculate the average power in the circuit.
The average power P in the circuit can be calculated using:
P=Vrms⋅Irms⋅cos(δϕ)
Where δϕ=ϕi−ϕv:
δϕ=π3−π6=π6
Calculating Vrms and Irms:
Vrms=V0√2=3√2,Irms=I0√2=2√2=√2
Now substituting into the power formula:
P=(3√2)⋅(√2)⋅cos(π6)
P=3⋅√32=3√32
Step 5: Calculate the resistance of the circuit.
Using the relationship between power and resistance:
P=I2rms⋅R
Substituting Irms=√2:
3√32=(√2)2⋅R
3√32=2R⟹R=3√34ohm
Step 6: Calculate the wattless component of current.
The wattless component of current is given by:
Iwattless=Irms⋅cos(ϕi)
Substituting Irms=√2 and ϕi=π3:
Iwattless=√2⋅cos(π3)=√2⋅12=√22=1√2
Summary of Results:
1. Impedance Z=1.5ohm (Correct)
2. Reactance cannot be determined (Incorrect)
3. Resistance R=3√34ohm (Correct)
4. Wattless component of current =1√2 (Correct)
Final Answer:
- The correct statements are:
- Impedance of the circuit is 1.5ohm.
- Resistance of the circuit is 3√34ohm.
- Wattless component of current is 1√2.
- Voltage: V=3sin(314t+π6)
- Current: I=2sin(315t+π3)
- Amplitude of voltage, V0=3
- Angular frequency of voltage, ωv=314
- Phase angle of voltage, ϕv=π6
- Amplitude of current, I0=2
- Angular frequency of current, ωi=315
- Phase angle of current, ϕi=π3
Z=V0I0
Substituting the values we have:
Z=32=1.5ohm
XL=ωLandXC=1ωC
However, we do not have the values of L and C provided in the problem, so we cannot calculate the reactance directly. Thus, we cannot confirm the reactance statement.
P=Vrms⋅Irms⋅cos(δϕ)
Where δϕ=ϕi−ϕv:
δϕ=π3−π6=π6
Vrms=V0√2=3√2,Irms=I0√2=2√2=√2
P=(3√2)⋅(√2)⋅cos(π6)
P=3⋅√32=3√32
P=I2rms⋅R
Substituting Irms=√2:
3√32=(√2)2⋅R
3√32=2R⟹R=3√34ohm
Iwattless=Irms⋅cos(ϕi)
Substituting Irms=√2 and ϕi=π3:
Iwattless=√2⋅cos(π3)=√2⋅12=√22=1√2
1. Impedance Z=1.5ohm (Correct)
2. Reactance cannot be determined (Incorrect)
3. Resistance R=3√34ohm (Correct)
4. Wattless component of current =1√2 (Correct)
- The correct statements are:
- Impedance of the circuit is 1.5ohm.
- Resistance of the circuit is 3√34ohm.
- Wattless component of current is 1√2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - D)
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - E)
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - B)
22 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A series LCR circuit is connected across a source of emf E =20sin(100πt−π6). The current from the supply is I =4sin(100πt+π12). Draw the impedance triangle for the circuit.
View SolutionA series L-C-R circuit is connected across an AC source V = 10sin[100πt−π6]. Current from the supply is I = 2sin[100πt+π12], What is the average power dissipated?
View SolutionA series L-C-R circuit is connected across an AC source E = 10sin[100πt−π6]. Current from the supply is I = 2sin[100πt+π12], What is the average power dissipated?
View SolutionIn a series LR circuit (L=3H,R=1.5Ω) and DC voltage =1V. Find current at T=2 seconds.
View SolutionIn y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
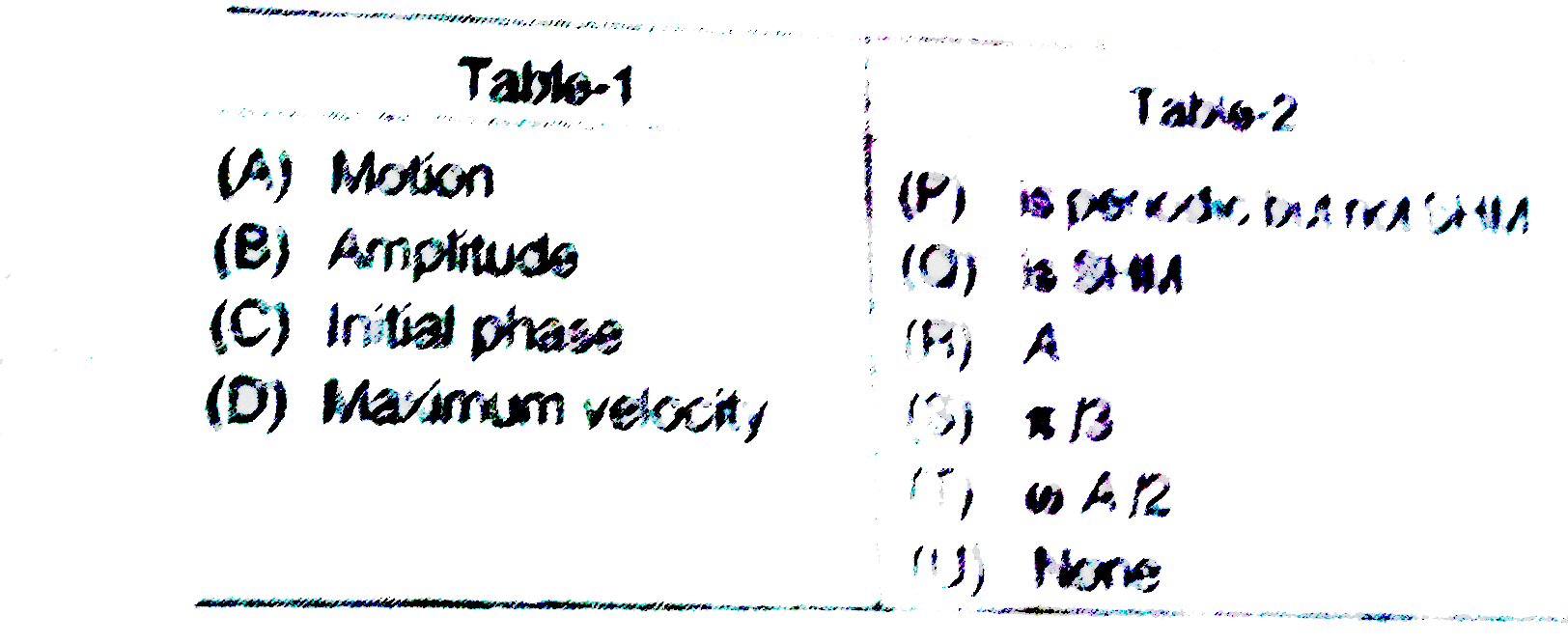
View SolutionIn an AC circuit, the current is given by i=5sin(100t−π2) and the AC potential is V=200sin(100t)volt. Then the power consumption is
View SolutionIn a series LCR circuit, an alternating emf (V) and current (I) are given by the equation V=V0sinωt,I=I0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
View SolutionIn an AC circuit, the applied potential difference and the current flowing are given by
V=20sin100t volt ,I=5sin(100t−π2) amp
The power consumption is equal to
View SolutionA resistance and inductance are connected in series across a voltage,
V=283sin314t
The current is found to be 4sin(314t−π/4). Find the value of the inductance and resistance.
View SolutionA resistance and inductance are connected in series across a voltage,
V=283sin314t
The current is found to be 4sin(314t−π/4). Find the value of the inductance and resistance.
View Solution
