Which of the following is not true ?
The number whose conjugate is 11−iis11+i
if sinx+icos2xandcosx−isin2x are conjugate to each other then number of values of x is zero
if x+ 1+iy and 2 + 3i are conjugate of each other then the value of x + y is -2.
2+I>3+i
The correct Answer is:D
To solve the problem of identifying which statement is not true among the given options, let's analyze each statement step by step.
Step 1: Analyze the First Statement
The first statement claims that the number whose conjugate is 11−i is 11+i.
1. Let z=11+i.
2. To find the conjugate z∗, we first rationalize z:
z=11+i⋅1−i1−i=1−i12+12=1−i2=12−12i
3. The conjugate z∗=12+12i.
4. Now, let's find z∗ directly from 11−i:
z∗=11−i⋅1+i1+i=1+i12+12=1+i2=12+12i
5. Since both calculations yield the same result, the first statement is true.
Step 2: Analyze the Second Statement
The second statement claims that if sinx+icos2x and cosx−isin2x are conjugates, then the number of values of x is zero.
1. Let z=sinx+icos2x.
2. The conjugate z∗=sinx−icos2x.
3. Set z∗=cosx−isin2x:
sinx−icos2x=cosx−isin2x
4. Equate the real and imaginary parts:
- Real: sinx=cosx
- Imaginary: −cos2x=−sin2x or cos2x=sin2x
5. The equations sinx=cosx gives x=π4+nπ and cos2x=sin2x gives 2x=π4+nπ.
6. There are solutions for x, hence the statement is false.
Step 3: Analyze the Third Statement
The third statement claims that if x+1+iy and 2+3i are conjugates, then x+y=−2.
1. Let z=x+1+iy.
2. The conjugate z∗=x+1−iy.
3. Set z∗=2+3i:
x+1−iy=2+3i
4. Equate the real and imaginary parts:
- Real: x+1=2 → x=1
- Imaginary: −y=3 → y=−3
5. Thus, x+y=1−3=−2, confirming the statement is true.
Step 4: Analyze the Fourth Statement
The fourth statement claims that 2+i is greater than 3+i.
1. For complex numbers z1=2+i and z2=3+i:
- Real part of z1 is 2 and of z2 is 3.
- Imaginary part of both is 1.
2. For z1>z2, both the real part and imaginary part must satisfy:
- 2>3 (false)
- 1>1 (false)
3. Since neither condition holds, the statement is false.
Conclusion
The only statement that is not true is the fourth statement.
The first statement claims that the number whose conjugate is 11−i is 11+i.
2. To find the conjugate z∗, we first rationalize z:
z=11+i⋅1−i1−i=1−i12+12=1−i2=12−12i
3. The conjugate z∗=12+12i.
4. Now, let's find z∗ directly from 11−i:
z∗=11−i⋅1+i1+i=1+i12+12=1+i2=12+12i
5. Since both calculations yield the same result, the first statement is true.
The second statement claims that if sinx+icos2x and cosx−isin2x are conjugates, then the number of values of x is zero.
2. The conjugate z∗=sinx−icos2x.
3. Set z∗=cosx−isin2x:
sinx−icos2x=cosx−isin2x
4. Equate the real and imaginary parts:
- Real: sinx=cosx
- Imaginary: −cos2x=−sin2x or cos2x=sin2x
5. The equations sinx=cosx gives x=π4+nπ and cos2x=sin2x gives 2x=π4+nπ.
6. There are solutions for x, hence the statement is false.
The third statement claims that if x+1+iy and 2+3i are conjugates, then x+y=−2.
2. The conjugate z∗=x+1−iy.
3. Set z∗=2+3i:
x+1−iy=2+3i
4. Equate the real and imaginary parts:
- Real: x+1=2 → x=1
- Imaginary: −y=3 → y=−3
5. Thus, x+y=1−3=−2, confirming the statement is true.
The fourth statement claims that 2+i is greater than 3+i.
- Real part of z1 is 2 and of z2 is 3.
- Imaginary part of both is 1.
2. For z1>z2, both the real part and imaginary part must satisfy:
- 2>3 (false)
- 1>1 (false)
3. Since neither condition holds, the statement is false.
The only statement that is not true is the fourth statement.
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -C) (objective Type Questions ( more thena one options are correct )
35 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -D) Linked comprehension Type Questions
14 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -A) (objective Type Questions ( one option is correct)
47 Videos
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-J) Objective type question (Aakash Challengers Questions)
4 Videos
- CONIC SECTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )
16 Videos
Similar Questions
Knowledge Check
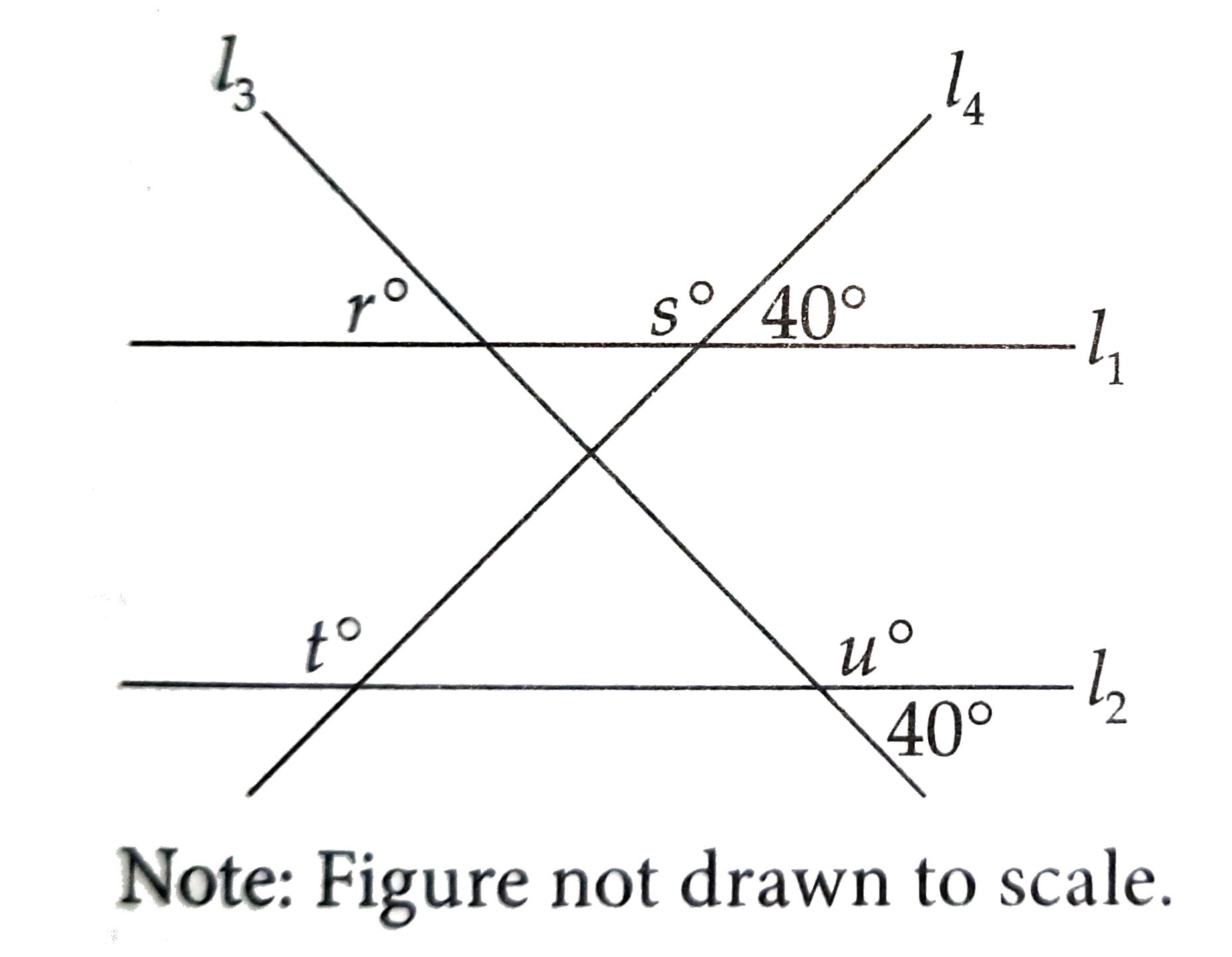
Which of the following must be true?Al1∣∣l2Bl3 bisects l4Cs=tDu=140∘Which of the following is a true statement ?
AIn all mammals, offspring develop within the femaleBAll mammals have hair and mammary glandsCAll mammals are land-dwelling formsDAll of the above
Which of the following is/are true ?
View SolutionWhich of the following is/are true ?
View SolutionWhich of the following is/are true ?
View SolutionWhich of the following is a true fruit ?
View SolutionWhich of the following is/are true?
View SolutionWhich of the following is/are true?
View Solution
