Find the radius of the circle escribed to the triangle ABC (Shown in the figure below) on the side BC if ∠NAB=30∘,∠BAC=30∘, AB=AC=5.
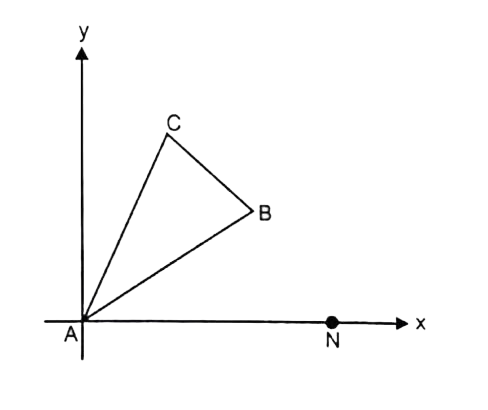
(10√2+5√3−5)(2−√3)2√2
(10√2+5√3+5)2√2(2−√3)
(10√2+5√3−5)2√2(2+√3)
(10√2+5√2+1)2√3(√3−1)
The correct Answer is:A
Step by step video & image solution for Find the radius of the circle escribed to the triangle ABC (Shown in the figure below) on the side BC if angleNAB=30^(@), angleBAC=30^(@), AB=AC=5. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
14 Videos
- SOLUTION OF TRIANGLESBOOK - VK JAISWAL ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-3 : Comprehension Type Problems
12 Videos
- SEQUENCE AND SERIES BOOK - VK JAISWAL ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- STRAIGHT LINES BOOK - VK JAISWAL ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems
10 Videos
Similar Questions
The radius of the circle touching two sides AB and AC of a triangle ABC and having its center on BC is equal to………………..
View SolutionIn the given figure, ABCDE is a pentagone inscribed in a circle such that AC is a diameter and side BC//AE. If ∠BAC=50∘, find ∠BCE,

View SolutionIf a circle is inscribed in right angled triangle ABC with right angle at B, show that the diameter of the circle is equal to AB+BC−AC.
View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View SolutionTwo circles having radii r1 and r2 passing through vertex A of triangle ABC. One of the circle touches the side BC at B and the other circle touches the side BC at C. If a =5cm and A=30∘ find √r1r2
View SolutionIf I1 is the centre of the escribed circle touching side BC of !ABC in which ∠A=60∘, then I1 A =
View SolutionIn a triangle ABC, right-angled at B, side BC = 20 cm and angle A= 30°. Find the length of AB.
View SolutionIn ΔABC,∠A=π3 and its incircle of unit radius. Find the radius of the circle touching the sides AB, AC internally and the incircle of ΔABC externally is x , then the value of x is
View SolutionIn a ΔABC, if (II1)2+(I2I3)2=λR2, where I denotes incentre, I1,I2andI3 denote centres of the circles escribed to the sides BC, CA and AB respectively and R be the radius of the circum circle of ΔABC. Find λ.
View Solution
