An ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. Let the probability that this point lies outside the ellipse be p. Then the value of 105 p is
The correct Answer is:70
To solve the problem, we need to find the probability p that a randomly chosen point within a circle lies outside an inscribed ellipse. We will then compute 105p.
1. Understanding the Problem:
We have a circle with radius a and an ellipse inscribed in it. The eccentricity of the ellipse is given as e=2√23.
2. Finding the Semi-Major and Semi-Minor Axes:
The relationship between the semi-major axis a and semi-minor axis b of the ellipse and its eccentricity e is given by:
e=√1−b2a2
Rearranging this, we find:
b2=a2(1−e2)
First, we calculate e2:
e2=(2√23)2=89
Therefore:
1−e2=1−89=19
Now substituting back:
b2=a2⋅19⟹b=a3
3. Calculating the Area of the Ellipse:
The area A of the ellipse is given by:
A=πab=πa⋅a3=πa23
4. Calculating the Area of the Circle:
The area Ac of the circle is:
Ac=πa2
5. Finding the Area of the Shaded Region:
The shaded region (area outside the ellipse but inside the circle) is:
Area of shaded region=Ac−A=πa2−πa23=πa2(1−13)=πa2⋅23
6. Calculating the Probability p:
The probability p that a point chosen randomly in the circle lies outside the ellipse is given by:
p=Area of shaded regionArea of circle=23πa2πa2=23
7. Calculating 105p:
Now we compute 105p:
105p=105⋅23=70
Final Answer:
Thus, the value of 105p is 70.
We have a circle with radius a and an ellipse inscribed in it. The eccentricity of the ellipse is given as e=2√23.
The relationship between the semi-major axis a and semi-minor axis b of the ellipse and its eccentricity e is given by:
e=√1−b2a2
Rearranging this, we find:
b2=a2(1−e2)
First, we calculate e2:
e2=(2√23)2=89
Therefore:
1−e2=1−89=19
Now substituting back:
b2=a2⋅19⟹b=a3
The area A of the ellipse is given by:
A=πab=πa⋅a3=πa23
The area Ac of the circle is:
Ac=πa2
The shaded region (area outside the ellipse but inside the circle) is:
Area of shaded region=Ac−A=πa2−πa23=πa2(1−13)=πa2⋅23
The probability p that a point chosen randomly in the circle lies outside the ellipse is given by:
p=Area of shaded regionArea of circle=23πa2πa2=23
Now we compute 105p:
105p=105⋅23=70
Thus, the value of 105p is 70.
Topper's Solved these Questions
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT SECTION-J (aakash challengers questions)
11 Videos
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT SECTION-H (multiple true-false type questions)
6 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
11 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - J) Aakash Challengers Questions
8 Videos
Similar Questions
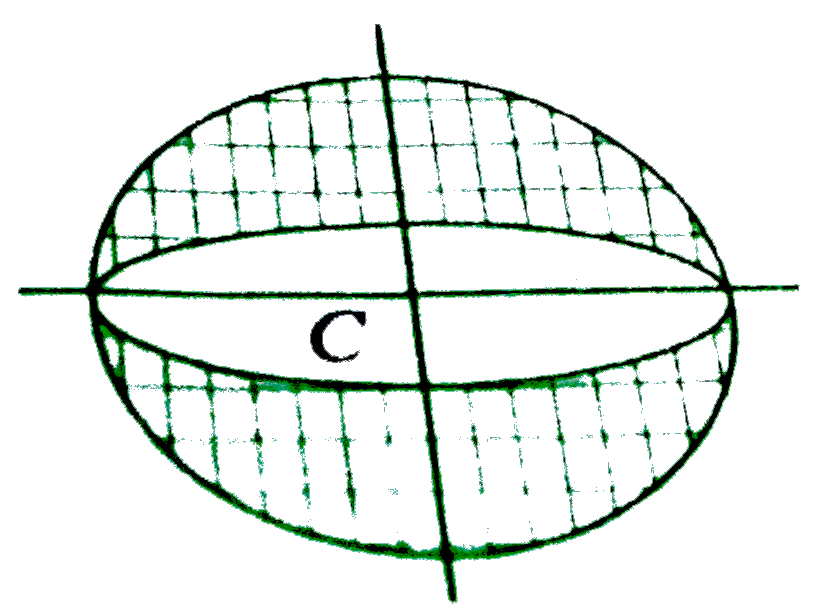
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
View SolutionAn ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is 23 then the eccentricity of the ellipse is: (A) 2√23 (B) √53 (C) 89 (D) 23
View SolutionA square is incribed in a circle . If p1 is the probability that a randomly chosen point of the circle lies within the square and p2 is the probability that the point lies outside the square then
View SolutionA point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is
View SolutionA circle of maximum area is inscribed in an ellipse. If p is the probability that a point within the ellipse chosen at random lies outside the circle, then the eccentricity of the ellipse is
View SolutionShow that the point (9,4) lies outside the ellipse
x210+y29=1
View SolutionThree points P,QandR are selected at random from the cirumference of a circle. Find the probability p that the point lie on a semi-circle
View SolutionA circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
View SolutionTen equally spaced point are lying on a circle, if p is the probability that a chosen chord is diameter of the circle, then 18p+2 is equal to ______.
View SolutionAn ellipse is inscribed in a reactangle and the angle between the diagonals of the reactangle is tan−1(2√2), then find the ecentricity of the ellipse
View Solution
