A charge Q is filled in a spherical volume of Radius R . Use the concept of energy density , find energy stored inside the charge volume.
To find the energy stored inside a spherical volume of radius R filled with a charge Q, we will use the concept of energy density in electrostatics. The energy density u is given by the formula:
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field.
1. Determine the Electric Field Inside the Sphere:
For a uniformly charged sphere, the electric field E at a distance x from the center (where x<R) is given by:
E=Q4πϵ0R3x
This is derived from Gauss's law.
2. Calculate the Energy Density:
Substitute the expression for E into the energy density formula:
u=12ϵ0(Q4πϵ0R3x)2
Simplifying this gives:
u=12ϵ0⋅Q216π2ϵ20R6x2=Q2x232π2ϵ0R6
3. Calculate the Total Energy Stored:
The total energy U stored in the sphere can be found by integrating the energy density over the volume of the sphere:
U=∫R0u⋅dV
The differential volume element dV for a spherical shell of radius x and thickness dx is:
dV=4πx2dx
Therefore, the total energy becomes:
U=∫R0Q2x232π2ϵ0R6⋅4πx2dx
Simplifying this:
U=Q28ϵ0R6∫R0x4dx
4. Evaluate the Integral:
The integral ∫R0x4dx can be computed as:
∫R0x4dx=R55
Substituting this back into the expression for U:
U=Q28ϵ0R6⋅R55=Q240ϵ0R
5. Final Result:
The energy stored inside the spherical volume filled with charge Q is:
U=Q240ϵ0R
For a uniformly charged sphere, the electric field E at a distance x from the center (where x<R) is given by:
E=Q4πϵ0R3x
This is derived from Gauss's law.
Substitute the expression for E into the energy density formula:
u=12ϵ0(Q4πϵ0R3x)2
Simplifying this gives:
u=12ϵ0⋅Q216π2ϵ20R6x2=Q2x232π2ϵ0R6
The total energy U stored in the sphere can be found by integrating the energy density over the volume of the sphere:
U=∫R0u⋅dV
The differential volume element dV for a spherical shell of radius x and thickness dx is:
dV=4πx2dx
Therefore, the total energy becomes:
U=∫R0Q2x232π2ϵ0R6⋅4πx2dx
Simplifying this:
U=Q28ϵ0R6∫R0x4dx
The integral ∫R0x4dx can be computed as:
∫R0x4dx=R55
Substituting this back into the expression for U:
U=Q28ϵ0R6⋅R55=Q240ϵ0R
The energy stored inside the spherical volume filled with charge Q is:
U=Q240ϵ0R
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE20videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A44videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)15videos
GRAVITATION
Similar Questions
A charge +Q is uniformly distributed in a spherical volume of radius R. A particle of charge +q and mass m projected with velocity v0 the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of v0 such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is
View SolutionA metal sphere of radius R is charged to a pontital V . (a ) Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R . (b )Show that the electrostatic field energy stored outside the sphere of radius 2R equals that stored within it .
View SolutionUsing the concept of energy density, find the total energy stored in a
a. parallel plate capacitor
b. charged spherical conductor.View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
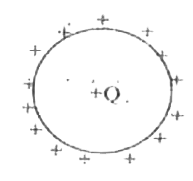 View Solution
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
 View Solution
View SolutionCalculate the self potential energy of charge q distributed over the surface of a hollow sphere of radius R. What happens to this self energy when R=0, or when the charge is an ideal point charge?
View SolutionA charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will
View SolutionSuppose a cube of volume 2mm3 is placed at the centre of a circular loop of radius 5 cm carrying current 2A.
Find the magnetic energy stored inside the cube.View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
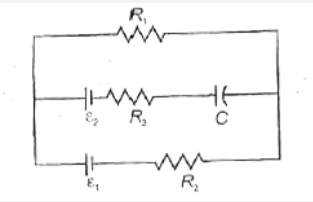 View Solution
View Solution

