Figure (A) and (B) show two resistors with resistances R1 and R2 connected in parallel and in series. The battery has a terminal voltage of e.

Suppose R1 and R2 are connected in parallel .
(a) Find the power delivered to each resistor.
(b) Show that the power used by each resistor is equal to the power supplied by the battery .
Suppose R1 and R2 are now connected in series
(c ) Find teh power delivered to each resistor.
(d) Show that the sum of the power by each resistor is equal to the power supplied by the battery.
(e ) Which configuration , parallelor series, uses more power ?
(a) When two resistors are connected in paralle, the current through each resistor is l1=εR1,l2=εR2
and the power delivered to each resistor is given by
P1=l21R1=ε2R1,P2=l22R2=ε2R2
(b) The total power delivered to the two resistors is
PR=P1+P2+ε2R1+ε2R2⇒ε2Req
where,
1Req=1R1+1R2⇒Req=R1R2R1+R2
is the equivalent resistance of the circuit .
On the other hand , the total power supplied by the battery is P=iε, where l=l1−l2 , as seen from the figure. Thus , P=l1ε+l2ε=(εR1)ε+(εR2)ε=ε2R1+ε2R2=ε2Req=PR as required by energy conservation.
(c ) When the two resistors are connected in series, the equivalent resistance becomes R′eq=R1+R2
and the current through the resistors are
l1=l2=l=εR1+R2
Therefore, the power delivered to each resistor is
P1=l21R1=(εR1+R2)2R1,P2=l22R2=(εR1+R2)2R2
Contrary to waht we have seen in the parallel case, when connected in series, the greater the resistance, the greater the fraction of the power delivered. Once again, if the loads are ligth bulbs, the one with greater resitance will be brighter.
(d) The total power delivered to the resistor is
P′R=P1+P2=(εR1+R2)2R1+(εR1+R2)2R2=ε2R1+R2=ε2R′eq
On the other hand, the power supplied by the battery is
P'=lε=(εR1+R2)ε=ε2R1+R2=ε2R′eq
Again, we see that P'=P′R as required by energy conservation.
(e ) Comparing the results obtained in (b) and (d), we see that
Pε=ε2R1+ε2R2>ε2R1+R2=P′ε
which means that the parallel connection uses more power. This is true since the equivalent resistance of two resistors connected in parallel is always than that connected in series.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Two resistors R1=60ΩandR2=90Ω are connected in parallel. If electric power consumed by the resistor R1 is 15 W, calculate the power consumed by the resistor R2
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View Solution
Knowledge Check
Two resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
A(800±1)ΩB(800±7)ΩC(200±7)ΩD(200±1)Ω
Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionIn Figure below, power developed in resistor R1 is 120W. Find the power developed in resistor R3.
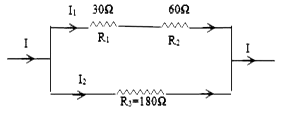
View SolutionShow by a diagram how two resistors R1andR2 are joined in parallel. Obtain an expression for the total resistance of the combination.
View Solution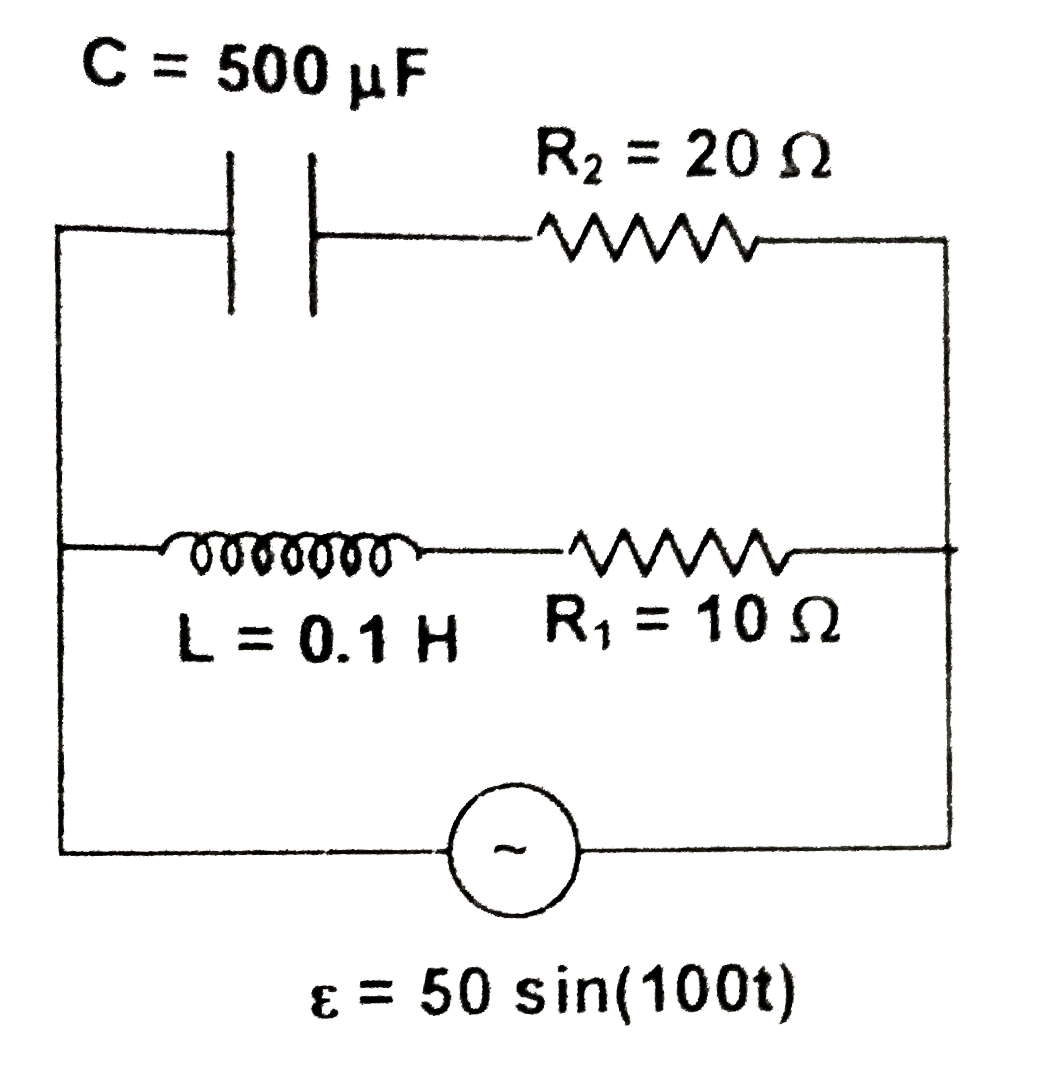
In the circuit shown the average power developed in the resistor R1 is
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionWhen two resistances R1andR2 are connected in series , they consume 12 W powers . When they are connected in parallel , they consume 50 W powers . What is the ratio of the powers of R1andR2 ?
View SolutionFor two resistors R1 and R2, connected in parallel, find the relative error in their equivalent resistance. if R1=(50±2)Ω and R2=(100±3)Ω.
View Solution
