Find the steady-state current l1 and l2 in the circuit drawn in figure. Also find the resistance of resistor R3 , that will give a steady -state current l3=50mA. Finally , determine the potential drop across the capacior. The values of the known elements are ε=6V,R1=100Ω,R2=80Ω, and C=2μF
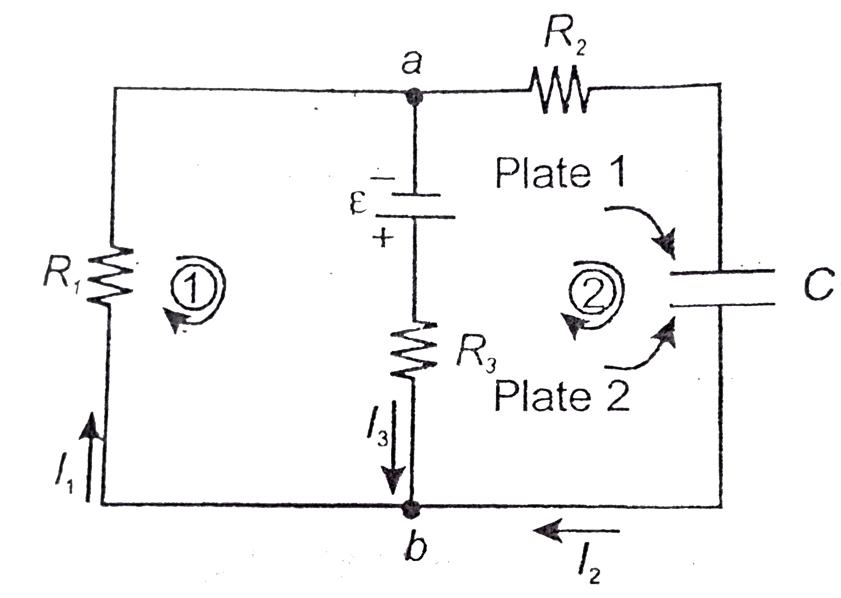
Strategy : A capacity acts as an open switch for steady-state current flow. Nevertheless, there is a voltage drop across the capacitor , because charge can build up on the capacitor plates under the impetus of the battery as the steady state is achieved . ( Once steady state is reached, there is no further build up of charge. ) We must accordingly include he capacitor in application of the loop rule, and we cannot simply ignore, for example , the loop (a-capacitor -b-a). There will therefore be two loop equations and one junction equation -with two junctions, there is always only one independent equation. With three equations, we will be able to solve for the three unknown l1,R2 and the potential drop across the capacitor.
We first write down the loop equations, remembering that the currents are constant in time, so that no current passes through the leg containing the capacitor, and l2=0 . This simplifies the independent junction (b) equation which reads
l1=l2+l2=l3
For the loop equations loop 1 gives
ε=l3R3−i1R1=0,
from which we obtain the resistance
R3=ε−l1R1l3=ε−l3R3l3=εl3−R1
Finally , the equation for loop 2 reads −l2R2+VC+l3R3−ε=0 where VC is the potential difference across the capacitor , and with l2=0 ,we get
VC=ε−l3R3
The numerical results are
R3=6V50mA=100Ω=6V50×10−3A−100Ω=20Ω
and VC=(6V)−(50×10−3A)(20Ω)=5V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
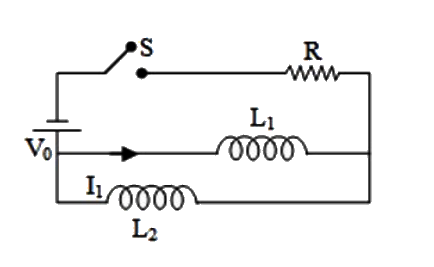
Find the steady - state current through L1 in the figure
View SolutionDetermine the voltage drop across the resistor R1 in the circuit given below with E = 65V, R_1 = 50 OmegaR_2 = 100 Omega, R_3 = 100 Omega, and R_4 300 Omega.

View SolutionDetermine the voltage drop across the resistor R1 in the circuit given below with E=65V,R1=50Ω,R2=100Ω,R3=100Ω and R4300Ω

View SolutionIn the circuit shown in figure, R(1)=1Ω,R2=2Ω,C1=1μF,C2=2μF and E=6V. Calculate charge on each capacitor in steady state
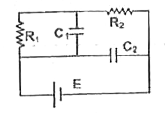
View SolutionIn the circuit shown in figure, R(1)=1Ω,R2=2Ω,C1=1μF,C2=2μF and E=6V. Calculate charge on each capacitor in steady state

View SolutionDetermine the voltage drop across the resistance R1 in the circuit given in Fig. 4.55 with ε=90V,R1=5kΩ,R2=5kΩ,R3=10kΩ and R4=10kΩ.
View SolutionIn the circuit shown in figure find:

a. the current in the 3.00Ω resistor,b. the unknown emfsE1 and E2 and c the resistance R.
View SolutionIn the circuit shown in figure find:

(a). the current in the 3.00Ω resistor,
(b) the unknown emfsE1 and E2 and
(c) the resistance R.
View SolutionFind the current in each wire.
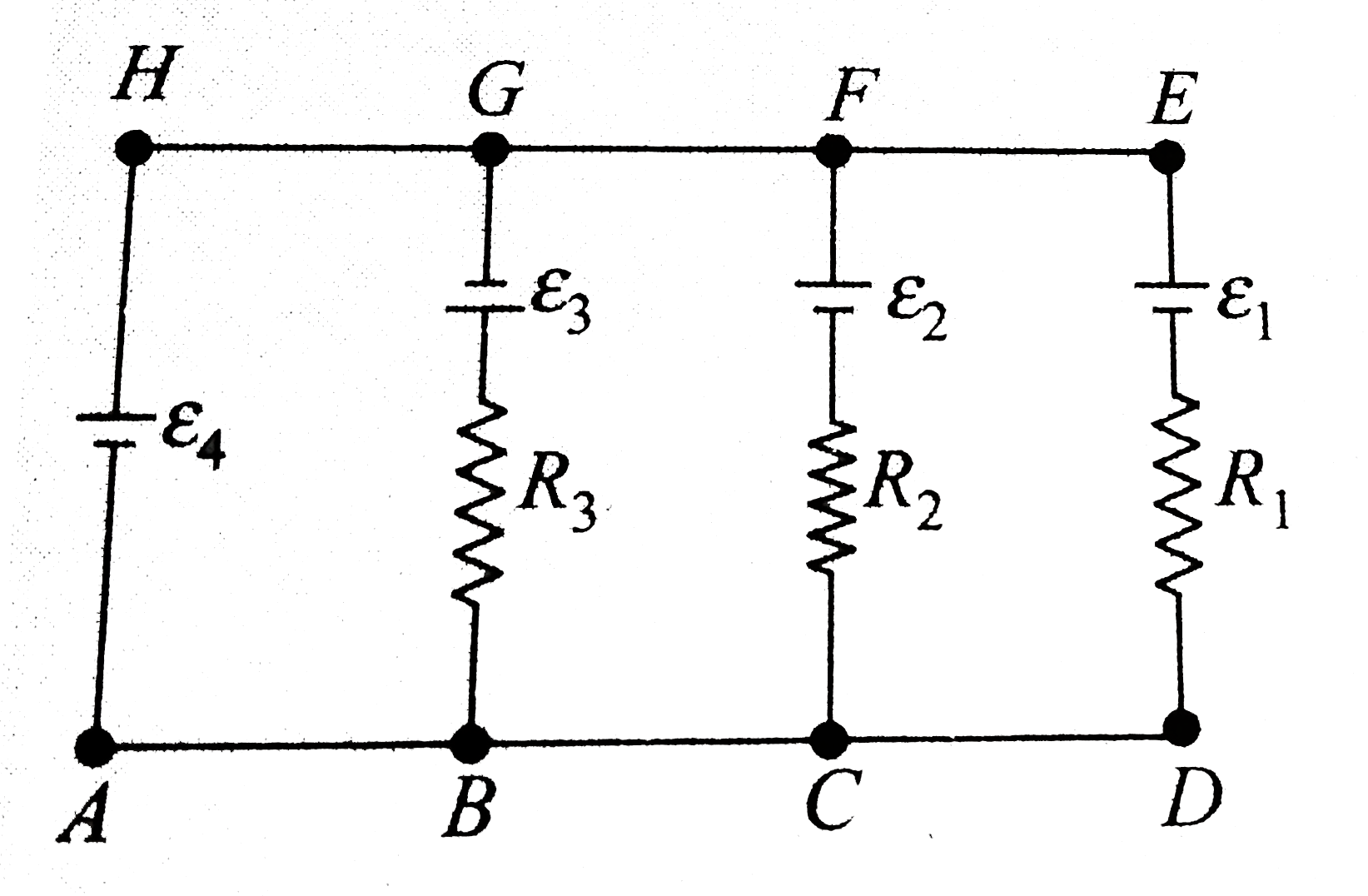
ε1=50V,ε2=40V
ε3=30V,ε4=10V
R1=2Ω,R2=2Ω
R3=1Ω
View SolutionFind current in R , L and 2L in steady state.
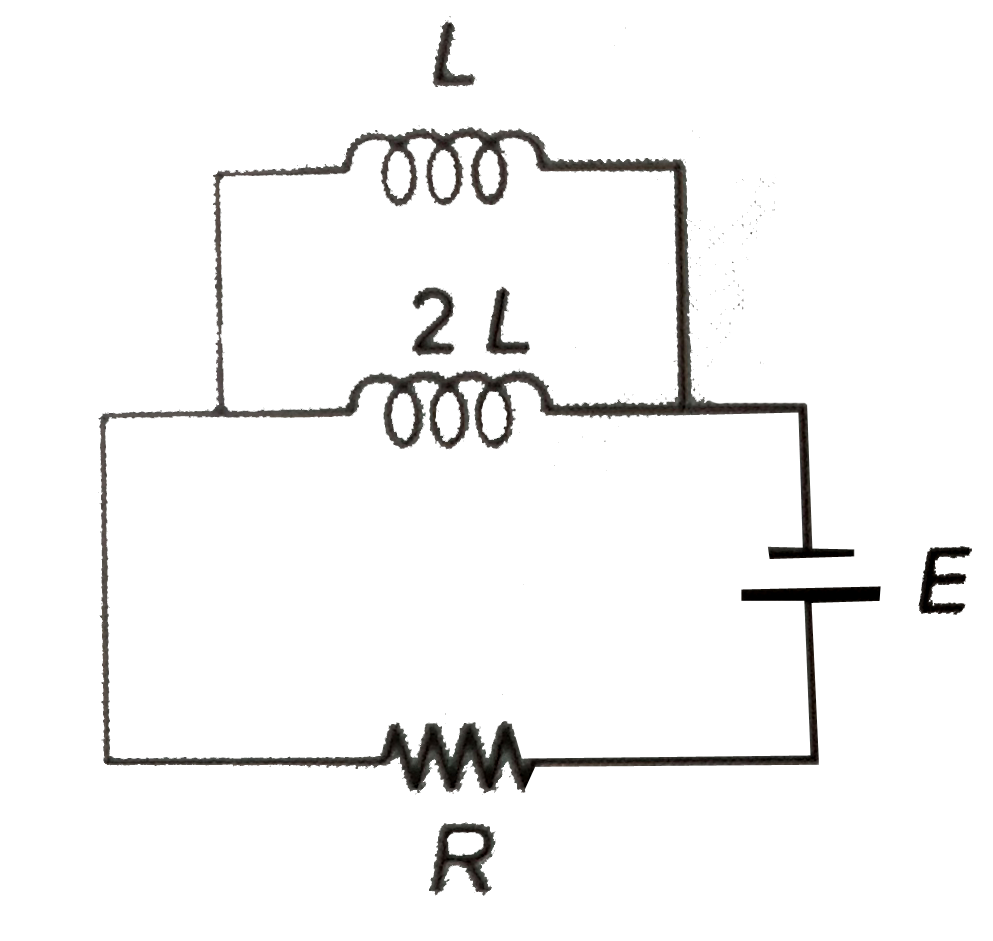
View Solution
