Two cells of emf E1 and E2(E1>E2) are connected in series to potentiometer for balancing length 625 cm . When polarity of E2 is reversed then balancing length becomes 125 cm. Then the ratio E1E2 is
3:2
3:1
5:1
2:1
The correct Answer is:1
To solve the problem, we need to analyze the situation with the two cells connected in series to a potentiometer and how the balancing lengths change with the reversal of the polarity of one of the cells.
1. Understanding the Initial Setup:
- When the two cells E1 and E2 are connected in series, the total EMF in the circuit is E1+E2.
- The balancing length on the potentiometer is given as 625 cm.
2. Using the Balancing Length:
- The potential difference across the potentiometer wire can be expressed in terms of the balancing length and the total EMF:
V=k⋅L
where V is the total potential difference, k is the potential gradient, and L is the balancing length.
- For the initial condition:
E1+E2=k⋅625
3. Reversing the Polarity of E2:
- When the polarity of E2 is reversed, the effective EMF becomes E1−E2.
- The new balancing length is given as 125 cm.
4. Setting Up the Equation for the New Condition:
- For the new condition:
E1−E2=k⋅125
5. Forming the System of Equations:
- We now have two equations:
1. E1+E2=k⋅625 (1)
2. E1−E2=k⋅125 (2)
6. Solving the System of Equations:
- We can add equations (1) and (2):
(E1+E2)+(E1−E2)=k⋅625+k⋅125
2E1=k⋅750
E1=k⋅7502=k⋅375
- Now, subtract equation (2) from equation (1):
(E1+E2)−(E1−E2)=k⋅625−k⋅125
2E2=k⋅500
E2=k⋅5002=k⋅250
7. Finding the Ratio E1E2:
- Now, we can find the ratio:
E1E2=k⋅375k⋅250=375250=32
Final Answer:
The ratio E1E2 is 32.
- When the two cells E1 and E2 are connected in series, the total EMF in the circuit is E1+E2.
- The balancing length on the potentiometer is given as 625 cm.
- The potential difference across the potentiometer wire can be expressed in terms of the balancing length and the total EMF:
V=k⋅L
where V is the total potential difference, k is the potential gradient, and L is the balancing length.
- For the initial condition:
E1+E2=k⋅625
- When the polarity of E2 is reversed, the effective EMF becomes E1−E2.
- The new balancing length is given as 125 cm.
- For the new condition:
E1−E2=k⋅125
- We now have two equations:
1. E1+E2=k⋅625 (1)
2. E1−E2=k⋅125 (2)
- We can add equations (1) and (2):
(E1+E2)+(E1−E2)=k⋅625+k⋅125
2E1=k⋅750
E1=k⋅7502=k⋅375
- Now, subtract equation (2) from equation (1):
(E1+E2)−(E1−E2)=k⋅625−k⋅125
2E2=k⋅500
E2=k⋅5002=k⋅250
- Now, we can find the ratio:
E1E2=k⋅375k⋅250=375250=32
The ratio E1E2 is 32.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
If the polarity of E2 is reversed, then
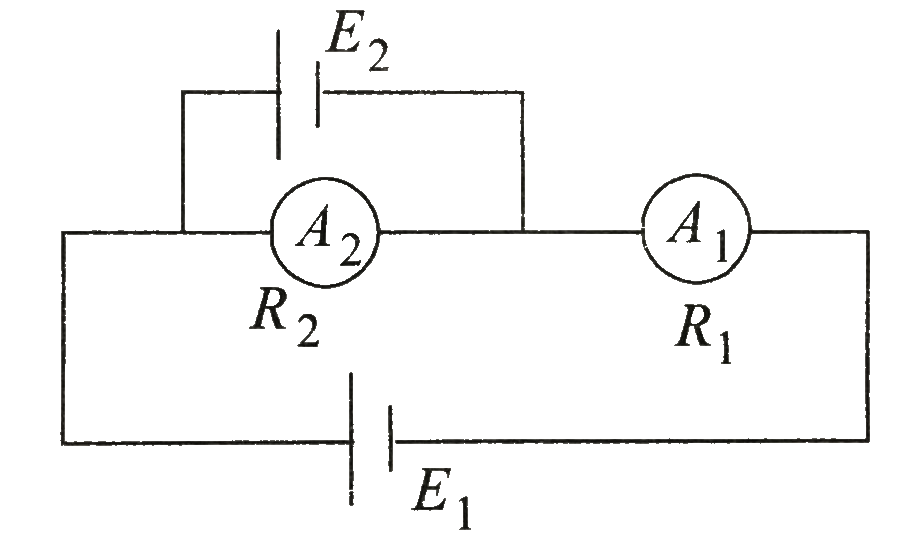
View SolutionIn a potentiometer experiment two cells of e.m.f. E1 and E2 are used in series and in conjunction and the balancing length is found to be 58 cm of the wire. If the polarity of E2 is reversed, then the balancing length becomes 29 cm . The ratio E1E2 of the e.m.f. of the two cells is
View SolutionTow cells of e.m.f E1 and E2 are joined in series and the balancing length of the potentiometer wire is 625 cm. If the terminals of E1 are reversed , the balancing length obtained is 125 cm. Given E2>E1,the ratio E1:E2 willbe
View SolutionTwo cells of E.M.F. E1 and E2(E2>E1) are connected in series in the secondary circuit of a potentiometer experiment for determination of E.M.F. The balancing length is found to be 825 cm. Now when the terminals to cell E1 are reversed, then the balancing length is found to be 225 cm. The ratio of E1 and E2 is
View SolutionTwo cells of emfs E1 and (E2(E1>E2) are connected as shows in Fig. 6.45.
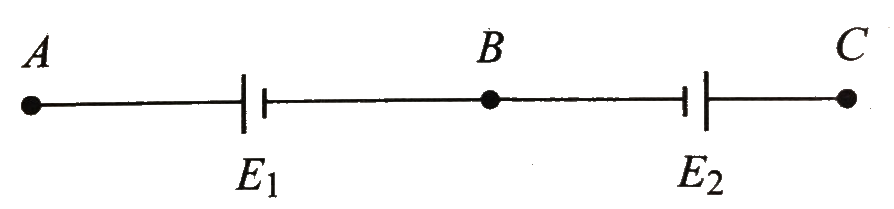
When a potentiometer is connected between A and B, the balancing length of the potentiometer wire is 300cm. On connecting the same potentiometer between A and C, the balancing length is 100cm. The ratio E1/E2 is
View SolutionTwo primary cells of emfs E1 and E2 are connected to the potentiometer wire AB as shown in the figure . If the balancing lengths for the two combinations of the cells are 250 cm and 400 cm , find the ratio of E1 and E2 .

View SolutionTwo cells of emf E1 and E2 are to be compared in a potentiometer (E1>E2) . When the cells are used in series correctly , the balancing length obtained is 400 cm. When they are used in series but E2 is connected with reverse polarities, the balancing obtaiend is 200cm. Ratio of emf of cells is
View SolutionTwo cells when connected in series are balanced on 6 m on a potentiometer. If the polarity one of these cell is reversed, they balance on 2m. The ratio of e.m.f of the two cells.
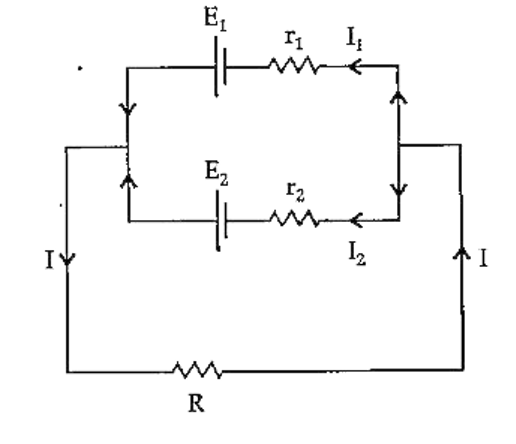
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionTwo cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
View Solution
