Determination of unknonw resistance in metre bridge is most accurate , when the balancing length is
50 cm
10 cm
20 cm
40 cm
The correct Answer is:1
To determine the unknown resistance in a meter bridge with maximum accuracy, we need to analyze the relationship between the balancing length and the percentage error in the measurement of the unknown resistance. Here’s a step-by-step solution:
Step 1: Understanding the Meter Bridge
The meter bridge is based on the principle of the Wheatstone bridge. The formula for the unknown resistance X in terms of the known resistance R and the balancing length L is given by:
XR=L100−L
Step 2: Rearranging the Formula
From the above equation, we can express X as:
X=L100−L×R
Step 3: Differentiating to Find dx
To find the accuracy of the measurement, we need to determine the change in X (denoted as dx) with respect to a change in L (denoted as dL). We will differentiate X with respect to L:
Using the quotient rule for differentiation, we have:
dx=R((100−L)⋅dL−L⋅(−dL)(100−L)2)
This simplifies to:
dx=R⋅(100−L+L)⋅dL(100−L)2=R⋅100⋅dL(100−L)2
Step 4: Finding the Relative Error
The relative error in the measurement of X is given by:
Relative Error=dxX
Substituting for dx and X:
Relative Error=R⋅100⋅dL(100−L)2L100−L⋅R
This simplifies to:
Relative Error=100⋅dLL⋅(100−L)
Step 5: Minimizing the Relative Error
To achieve maximum accuracy, we need to minimize the relative error. This can be done by maximizing the denominator L⋅(100−L).
Step 6: Finding the Maximum
Let f(L)=L⋅(100−L)=100L−L2. To find the maximum value, we differentiate f(L):
f′(L)=100−2L
Setting f′(L)=0:
100−2L=0⟹L=50
Step 7: Confirming Maximum
To confirm that this is a maximum, we check the second derivative:
f′′(L)=−2
Since f′′(L)<0, this indicates that L=50 cm is indeed a maximum.
Conclusion
Thus, the determination of unknown resistance in a meter bridge is most accurate when the balancing length is:
50 cm
The meter bridge is based on the principle of the Wheatstone bridge. The formula for the unknown resistance X in terms of the known resistance R and the balancing length L is given by:
From the above equation, we can express X as:
To find the accuracy of the measurement, we need to determine the change in X (denoted as dx) with respect to a change in L (denoted as dL). We will differentiate X with respect to L:
The relative error in the measurement of X is given by:
To achieve maximum accuracy, we need to minimize the relative error. This can be done by maximizing the denominator L⋅(100−L).
Let f(L)=L⋅(100−L)=100L−L2. To find the maximum value, we differentiate f(L):
To confirm that this is a maximum, we check the second derivative:
Thus, the determination of unknown resistance in a meter bridge is most accurate when the balancing length is:
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
If the resistance of potentiometer wire is 15r then calculate the balance length l
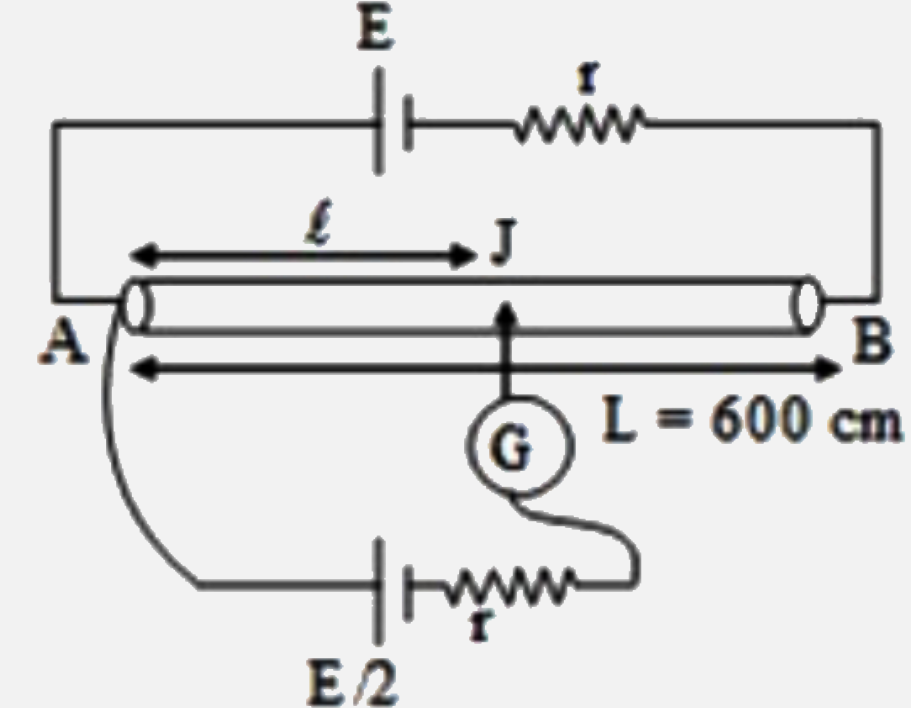
View SolutionIn an experiment on the measurement of internal resistance of as cell by using a potentionmeter, when the key K is kept open then balancing length is obtained at y metre. When the key K is closed and some resistance R is inserted in the resistance box, then the balancing length is found to be x metre. Then the internal resistance is
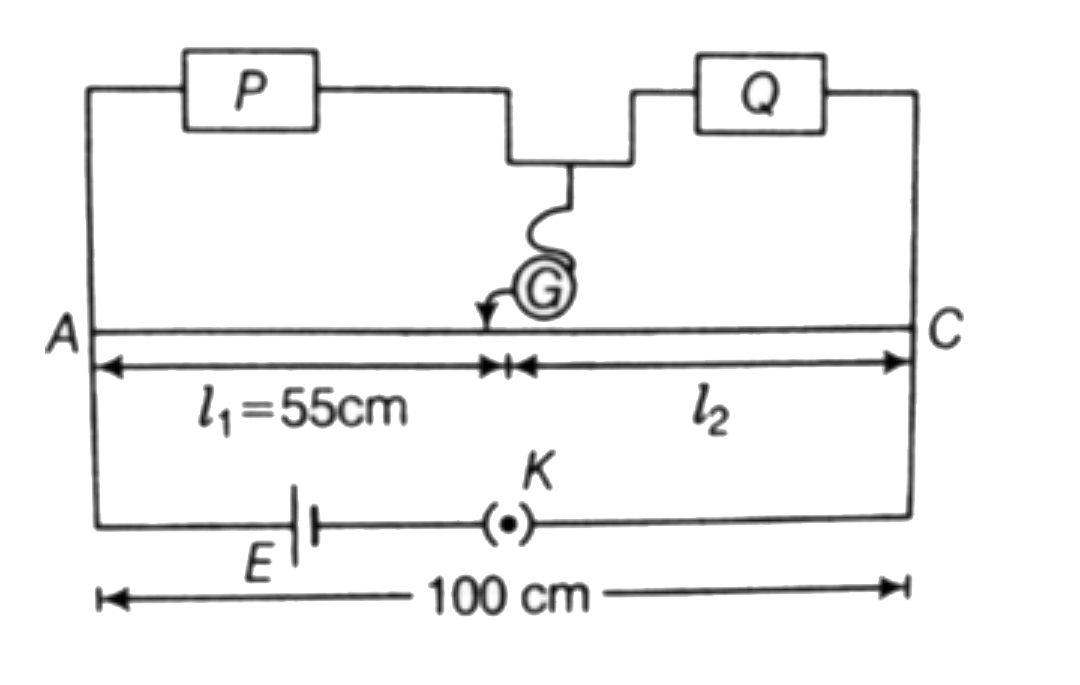
View SolutionIn a meter bridge experiment, resistances are connected as shown in figure. The balancing length l1=55cm. Now, an unknown resistance x is connected in series with P and the new balancing length is found to be 75 cm. What is the value of The value of 11x (in ohm)? (Given, P=4Ω)
View SolutionWhen a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View SolutionShow that the percentage error in the measurement of resistance by a metre bridge is minimum when the null point is near about the centre of the wire.
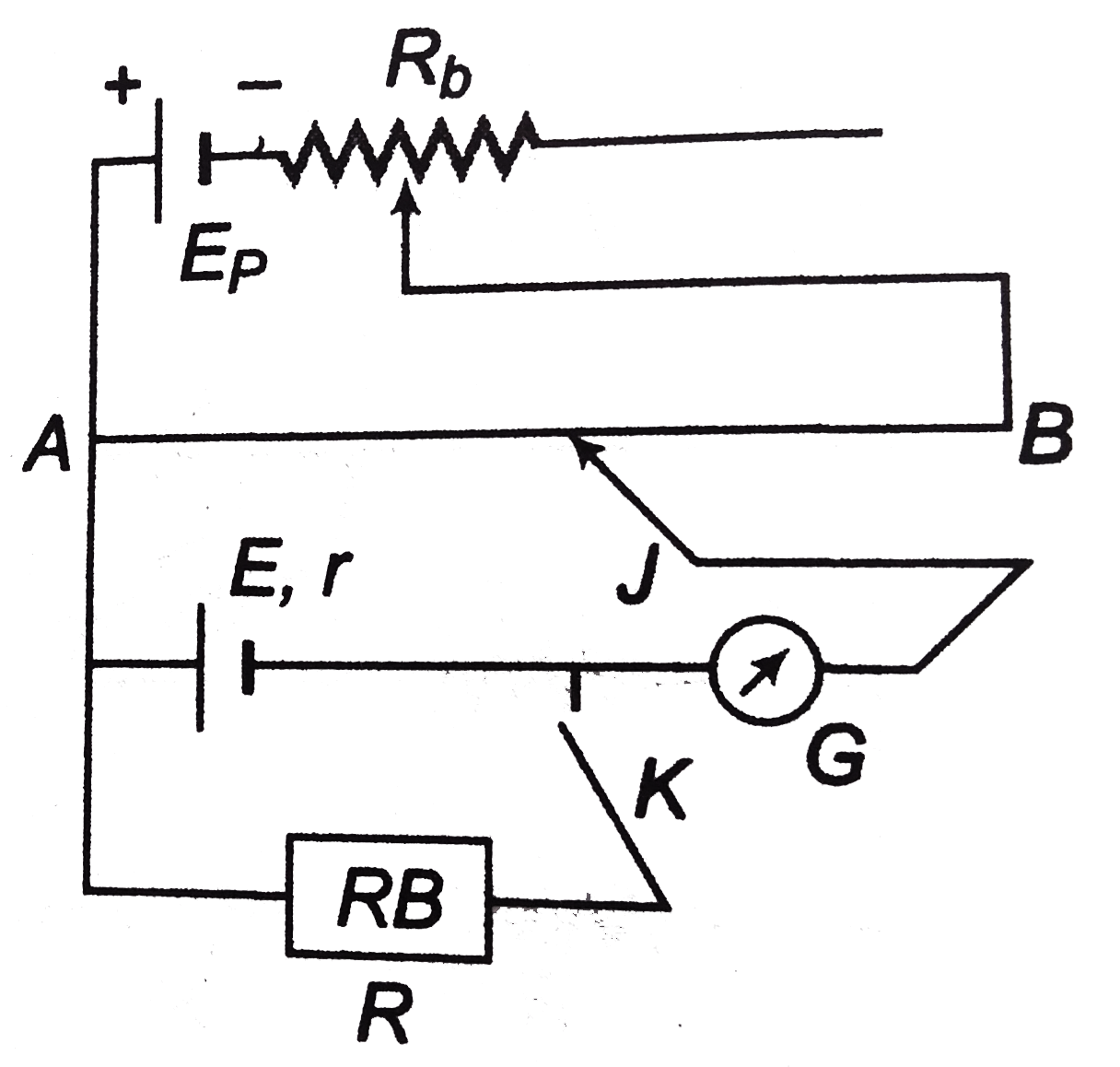
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
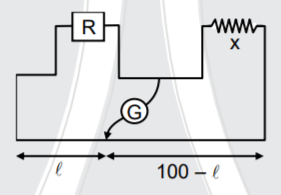
View SolutionIf in a meter bridge experiment, the balancing length l was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is

View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionIn meter bridge experiment if, resistance S in resistance box =300Ω then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of unknown wire is 31.4cm. The specific resistivity of the wire should be
View Solution
