A man of 50kg mass is standing in a gravity free space at a height of 10m above the floor. He throws a stone of 0.5kg mass downwards with a speed 2m/s. When the stone reaches the floor, the distance of the man above the floor will be
20 m
9.9 m
10.1 m
10 m
To solve the problem step by step, we will analyze the situation using the principles of conservation of momentum and kinematics.
Step 1: Understand the initial conditions
The man and the stone are initially at a height of 10 meters above the floor. The man has a mass of 50 kg and the stone has a mass of 0.5 kg. The stone is thrown downwards with a speed of 2 m/s.
Hint: Identify the initial conditions and the direction of motion for both the man and the stone.
Step 2: Conservation of momentum
Since there are no external forces acting on the system (man + stone), the total momentum of the system before and after the stone is thrown must be conserved.
- Initial momentum (P_initial) = 0 (both the man and stone are at rest).
- After the stone is thrown, let the velocity of the man be Vm and the velocity of the stone be Vs=−2m/s (negative because it's downward).
Using the conservation of momentum:
Pinitial=Pfinal
0=ms⋅Vs+mm⋅Vm
Substituting the values:
0=(0.5kg)⋅(−2m/s)+(50kg)⋅Vm
Hint: Write down the conservation of momentum equation and substitute the known values.
Step 3: Solve for the man's velocity
Rearranging the equation gives:
(50kg)⋅Vm=1kg m/s
Vm=150m/s=0.02m/s
This velocity is positive, indicating that the man moves upwards.
Hint: Isolate Vm to find the man's velocity after throwing the stone.
Step 4: Calculate the time taken for the stone to reach the floor
Using the formula for distance in uniform motion (since there is no acceleration):
s=ut+12at2
Here, s=10m, u=−2m/s, and a=0 (no acceleration in gravity-free space). Thus, the equation simplifies to:
10=−2t
Solving for t:
t=102=5s
Hint: Use the kinematic equation for uniform motion to find the time taken for the stone to reach the floor.
Step 5: Calculate the distance traveled by the man in that time
The distance traveled by the man while the stone is falling can be calculated using:
Distance=Vm⋅t
Substituting the values:
Distance=(150m/s)⋅(5s)=550=0.1m
Hint: Use the formula for distance traveled with constant velocity to find how far the man moves upwards.
Step 6: Calculate the final height of the man above the floor
Initially, the man was at a height of 10 m. After moving upwards by 0.1 m, his new height above the floor is:
New height=10m+0.1m=10.1m
Hint: Add the distance moved by the man to his initial height to find the final height above the floor.
Final Answer
The distance of the man above the floor when the stone reaches the floor is 10.1 meters.
The man and the stone are initially at a height of 10 meters above the floor. The man has a mass of 50 kg and the stone has a mass of 0.5 kg. The stone is thrown downwards with a speed of 2 m/s.
Since there are no external forces acting on the system (man + stone), the total momentum of the system before and after the stone is thrown must be conserved.
- After the stone is thrown, let the velocity of the man be Vm and the velocity of the stone be Vs=−2m/s (negative because it's downward).
Pinitial=Pfinal
0=ms⋅Vs+mm⋅Vm
Substituting the values:
0=(0.5kg)⋅(−2m/s)+(50kg)⋅Vm
Rearranging the equation gives:
(50kg)⋅Vm=1kg m/s
Vm=150m/s=0.02m/s
This velocity is positive, indicating that the man moves upwards.
Using the formula for distance in uniform motion (since there is no acceleration):
s=ut+12at2
Here, s=10m, u=−2m/s, and a=0 (no acceleration in gravity-free space). Thus, the equation simplifies to:
10=−2t
Solving for t:
t=102=5s
The distance traveled by the man while the stone is falling can be calculated using:
Distance=Vm⋅t
Substituting the values:
Distance=(150m/s)⋅(5s)=550=0.1m
Initially, the man was at a height of 10 m. After moving upwards by 0.1 m, his new height above the floor is:
New height=10m+0.1m=10.1m
The distance of the man above the floor when the stone reaches the floor is 10.1 meters.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
In a gravity free space, man of mass M standing at a height h above the floor, throws a ball of mass m straight down with a speed u. When the ball reaches the floor, the distance of the man above the floor will be.
View SolutionA man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
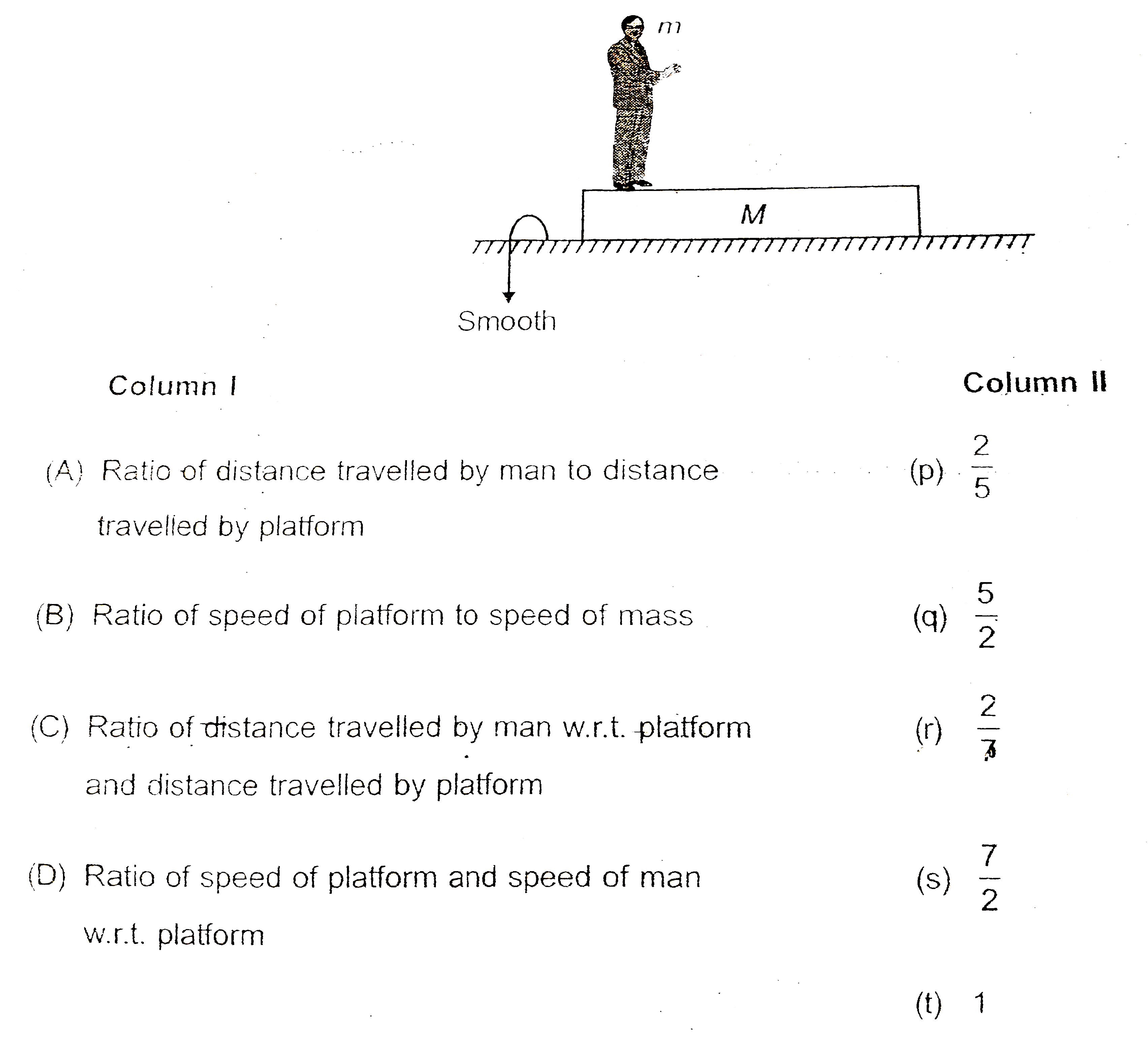
View SolutionA box of 50 kg is lifted by a man of mass 60 kg to a height of 50 m. Calculate the work done by the man.
View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View SolutionA boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
View SolutionA boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA ball of mass 2 kg is gently pushed off the edge of a tabletop that is 1.8 m above the floor. Find the speed of the ball as it strikes the floor.
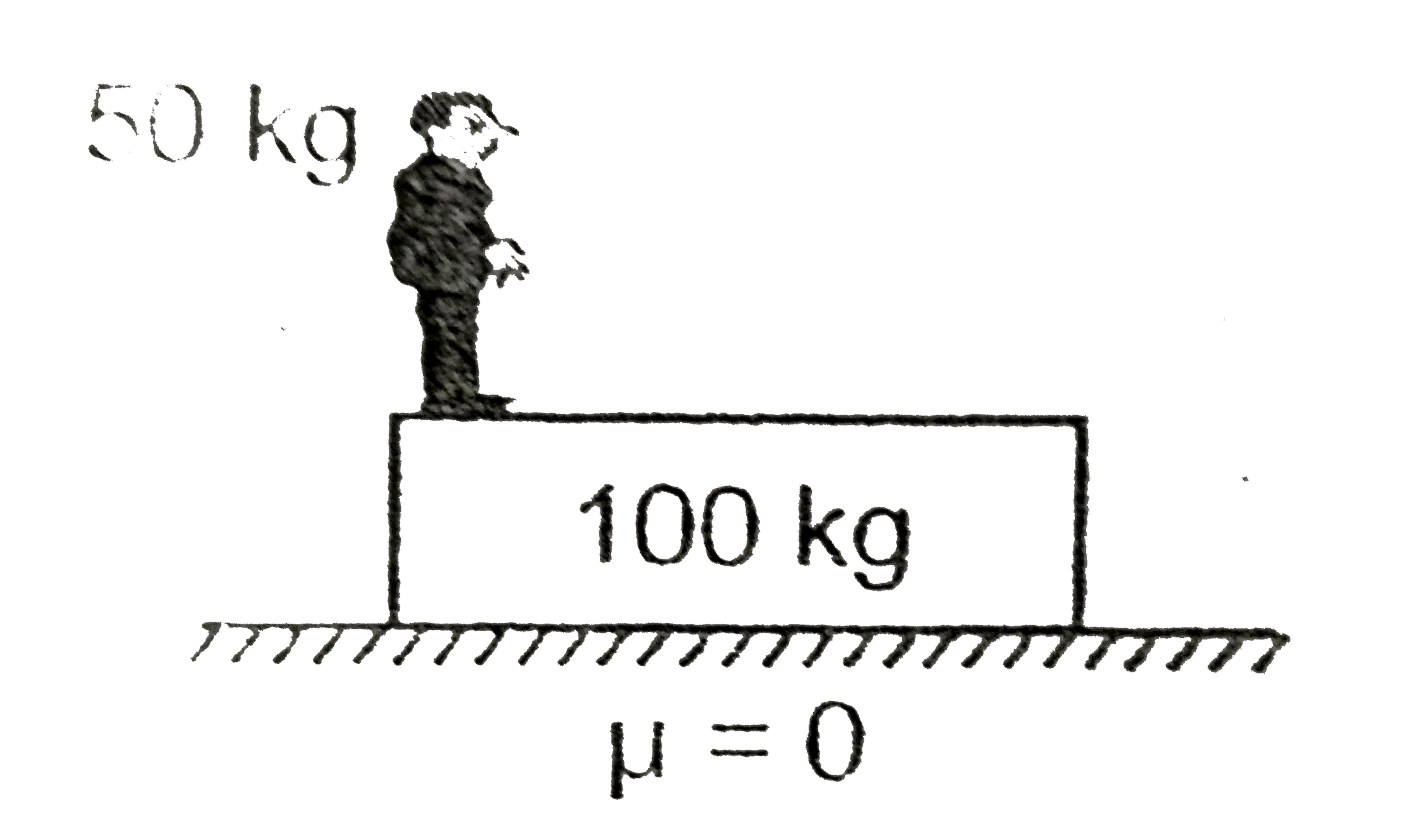
View SolutionA man of mass 50kg us standing on a 100kg plank kept on a fricitonless horizontal floor. Initially both are at rest. If the man starts walking on the plank with speed 6m/s towards right relative to the plank, then amount of muscle energy spent by the man is
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View Solution
