A lift of mass 1000 kg which is moving with an acceleration of 1ms−2 in upward direction , then the tension developed in string which is connected to lift is ___________
9800 N
10,800 N
11,000 N
10,000 N
To find the tension in the string connected to the lift, we can use Newton's second law of motion. Here are the steps to solve the problem:
Step 1: Identify the forces acting on the lift
The forces acting on the lift are:
- The gravitational force (weight) acting downwards, which is given by Fg=mg, where m is the mass of the lift and g is the acceleration due to gravity.
- The tension T in the string acting upwards.
Step 2: Write down the known values
- Mass of the lift, m=1000kg
- Acceleration of the lift, a=1m/s2
- Acceleration due to gravity, g=10m/s2 (approximated for calculations)
Step 3: Apply Newton's second law
According to Newton's second law, the net force acting on the lift is equal to the mass of the lift multiplied by its acceleration:
Net Force=ma
The net force can also be expressed as the difference between the tension and the gravitational force:
T−mg=ma
Step 4: Rearrange the equation to solve for tension T
Rearranging the equation gives:
T=mg+ma
Step 5: Substitute the known values into the equation
Now, substituting the known values:
T=(1000kg×10m/s2)+(1000kg×1m/s2)
T=10000N+1000N
T=11000N
Step 6: Conclusion
The tension developed in the string connected to the lift is 11000N.
---
The forces acting on the lift are:
- The gravitational force (weight) acting downwards, which is given by Fg=mg, where m is the mass of the lift and g is the acceleration due to gravity.
- The tension T in the string acting upwards.
- Mass of the lift, m=1000kg
- Acceleration of the lift, a=1m/s2
- Acceleration due to gravity, g=10m/s2 (approximated for calculations)
According to Newton's second law, the net force acting on the lift is equal to the mass of the lift multiplied by its acceleration:
Net Force=ma
T−mg=ma
Rearranging the equation gives:
T=mg+ma
Now, substituting the known values:
T=(1000kg×10m/s2)+(1000kg×1m/s2)
T=10000N+1000N
T=11000N
The tension developed in the string connected to the lift is 11000N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View SolutionA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA 60kg man is inside a lift which is moving up with an acceleration of 2.45ms−2. The apparent percentage change in his weight is,
View SolutionA man weighing 60 kg is in a lift moving down with an acceleration of 1.8 ms−2. The force exerted by the floor on him is
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
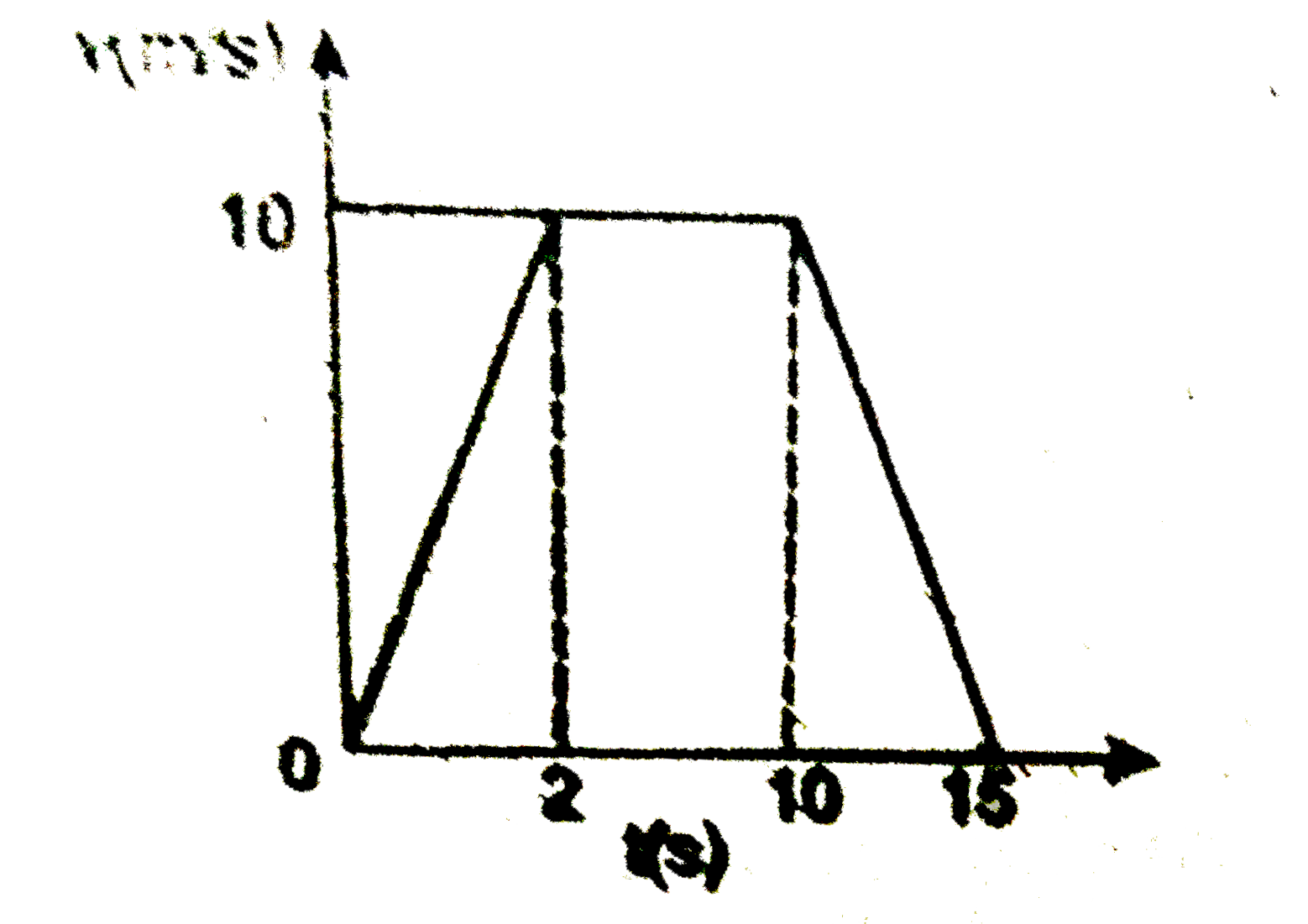
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
View Solution
