Figure shows a composite system of two uniform rods of lengths as indicated. Then the coordinate of the center of mass of the system of rods are

(L2,2L3)
(L4,2L3)
(L6,2L3)
(L6,L3)
The correct Answer is:C
Step by step video & image solution for Figure shows a composite system of two uniform rods of lengths as indicated. Then the coordinate of the center of mass of the system of rods are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find the velocity of center of mass of the system shown in the figure.

View SolutionThe x and y coordinates of the center of mass of the three-particle system shown below are :
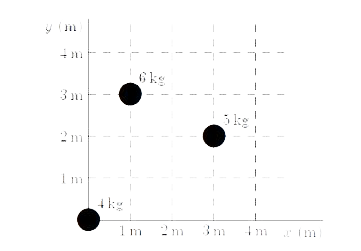
View SolutionIf three rods of same mass are placed as shown in the figure, the co-ordinates of the centre of mass of the system are
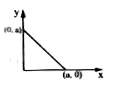
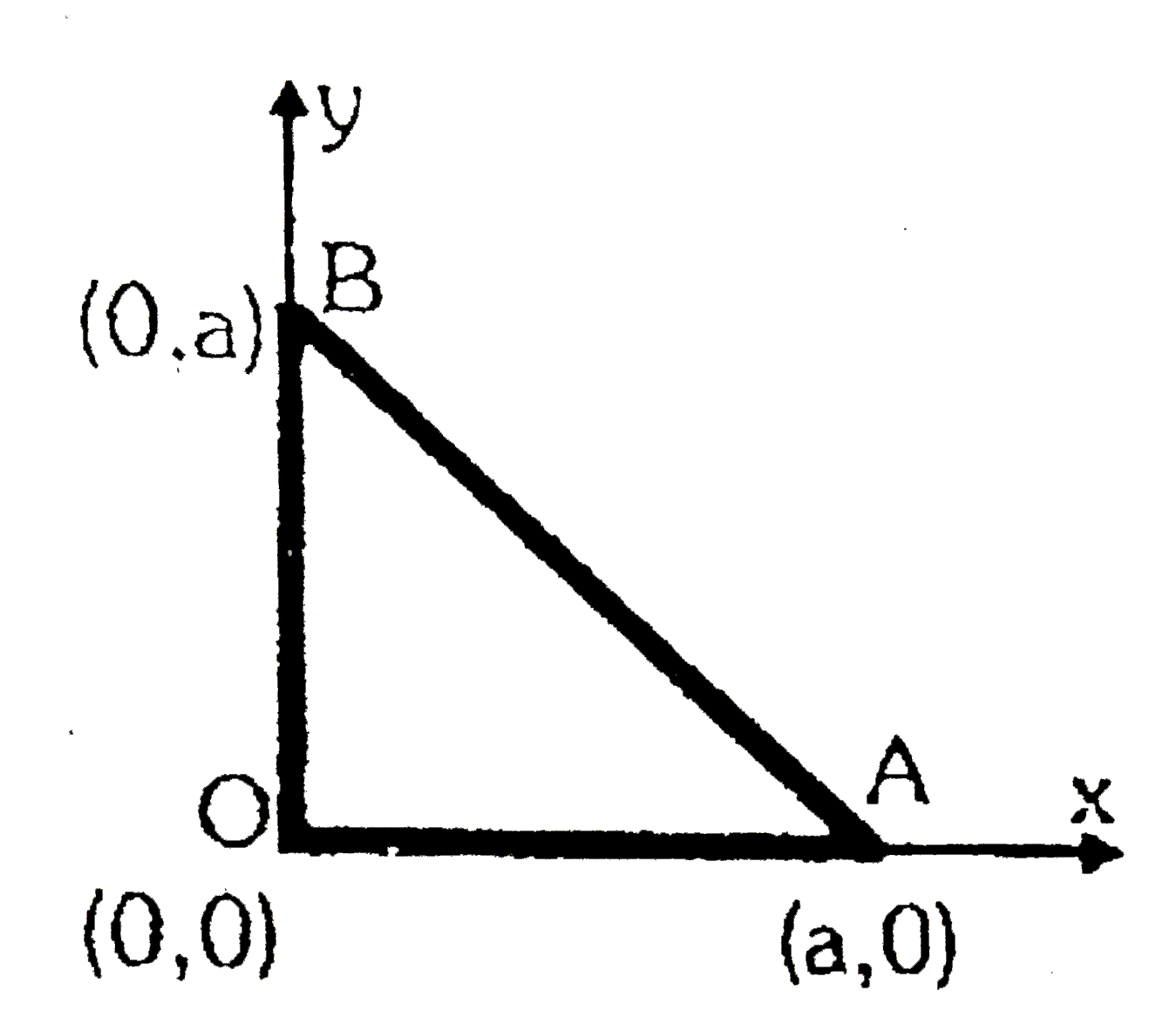
View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
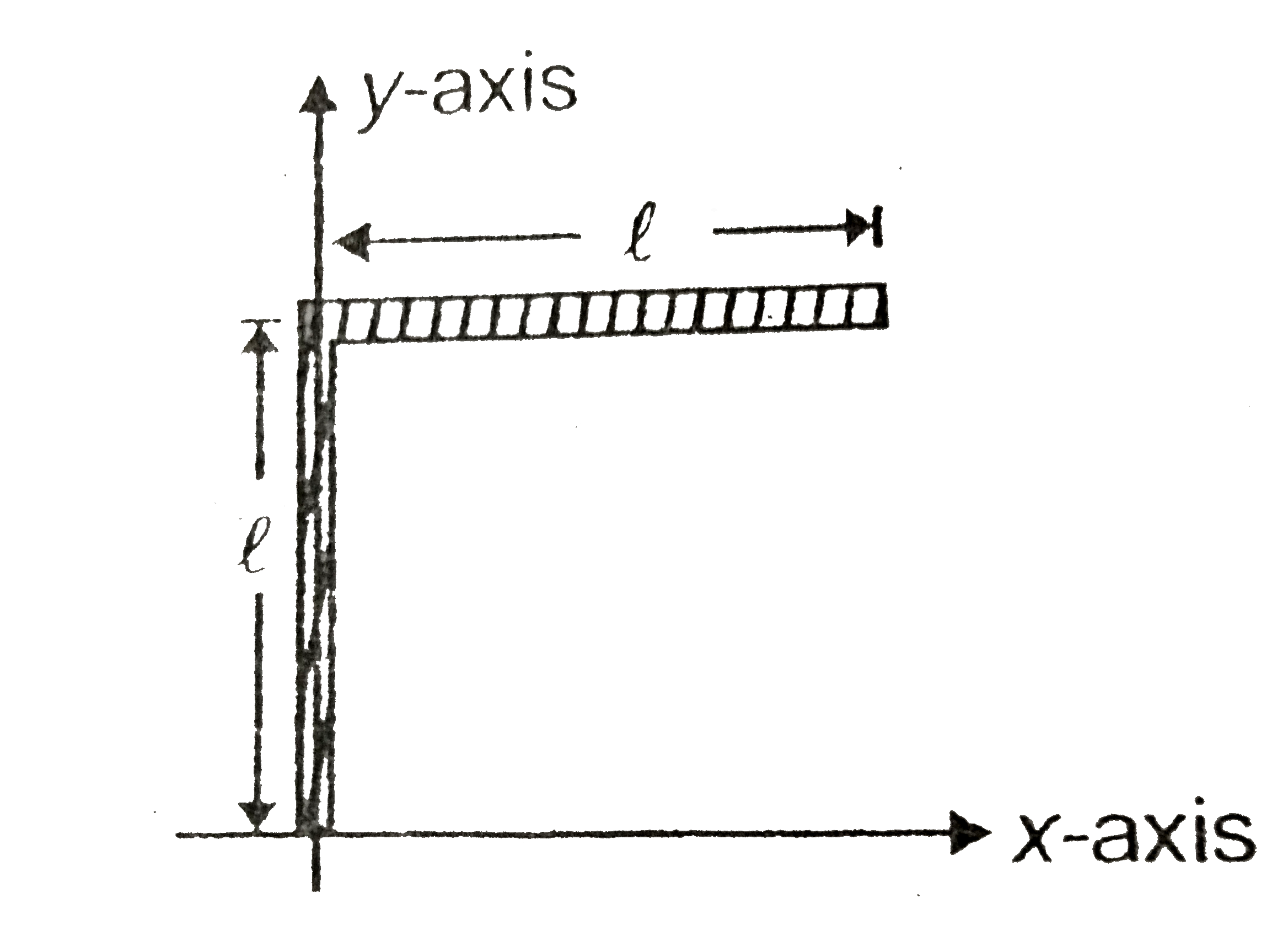
View SolutionThree rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.
View SolutionThree rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.

View SolutionA system of two identical, uniform discs with identical circular cavities, is shown in the figure. Different relevant coordinates are given in the figure. The coordinates of the centre of mass of the system are
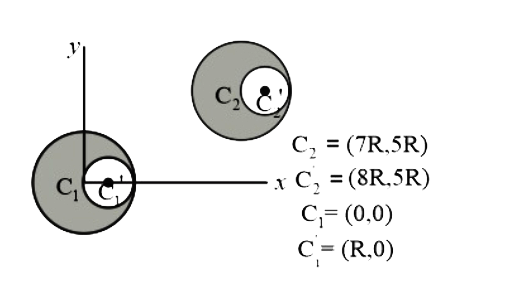
View SolutionA system of two identical, uniform discs with identical circular cavities, is shown in the figure. Different relevant coordinates are given in the figure. The coordinates of the centre of mass of the system are

View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
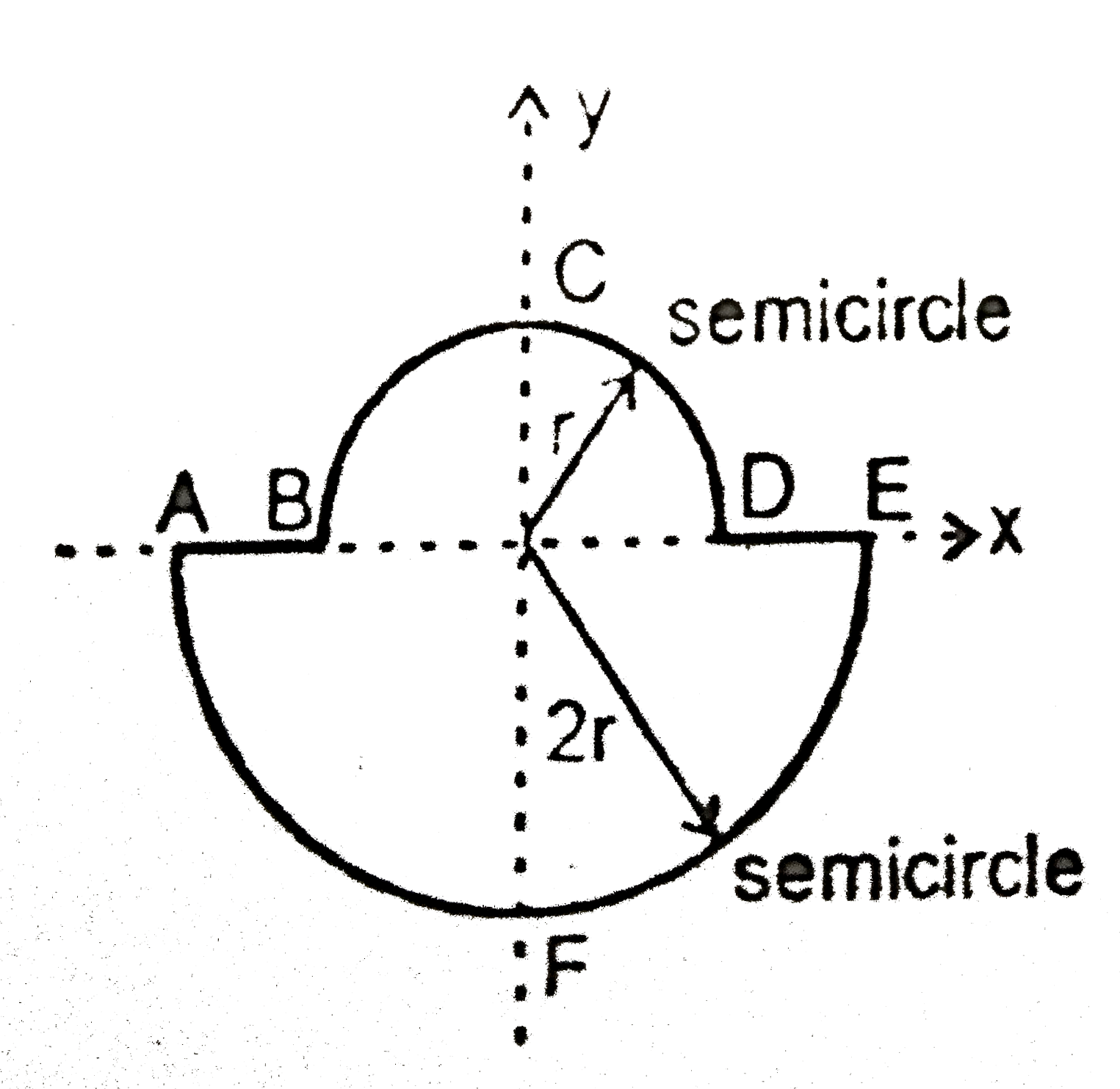
View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of co-ordinate system. If current I is flowing through each ring, then the magnitude of the magnetic field at the common centre is
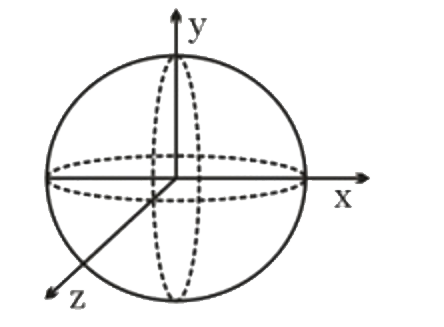
View Solution
