A uniform disc rotating freely about a vertical axis makes 90 rpm. A small piece of wax of mass m gram falls vertically on the disc and sticks to it at a distance rcm from the axis. If number of rotations per minute reduces to 60, find the moment of inertia of the disc.
m2
32mr2
2mr2
3mr2
The correct Answer is:C
To solve the problem, we will use the principle of conservation of angular momentum. The steps are as follows:
Step 1: Understand the initial and final conditions
- The initial angular velocity of the disc, ωi, is given as 90 rpm.
- The final angular velocity of the disc after the wax sticks to it, ωf, is given as 60 rpm.
Step 2: Convert angular velocities from rpm to rad/s
To apply the conservation of angular momentum, we need to convert the angular velocities from revolutions per minute (rpm) to radians per second (rad/s).
ωi=90rpm=90×2π60rad/s=9.42rad/s
ωf=60rpm=60×2π60rad/s=6.28rad/s
Step 3: Set up the conservation of angular momentum equation
According to the conservation of angular momentum:
Li=Lf
Where:
- Li is the initial angular momentum.
- Lf is the final angular momentum.
The initial angular momentum Li can be expressed as:
Li=I⋅ωi
Where I is the moment of inertia of the disc.
The final angular momentum Lf can be expressed as:
Lf=(I+mr2)⋅ωf
Where m is the mass of the wax and r is the distance from the axis.
Step 4: Write the equation using the conservation of angular momentum
Setting the initial and final angular momentum equal gives us:
I⋅ωi=(I+mr2)⋅ωf
Step 5: Substitute the known values
Substituting the values of ωi and ωf:
I⋅9.42=(I+mr2)⋅6.28
Step 6: Rearranging the equation
Expanding the right side:
I⋅9.42=I⋅6.28+mr2⋅6.28
Rearranging gives:
I⋅9.42−I⋅6.28=mr2⋅6.28
I(9.42−6.28)=mr2⋅6.28
Step 7: Solve for the moment of inertia I
Calculating 9.42−6.28:
I⋅3.14=mr2⋅6.28
Thus,
I=mr2⋅6.283.14
Since 6.28/3.14=2:
I=2mr2
Final Answer
The moment of inertia of the disc is:
I=2mr2
- The initial angular velocity of the disc, ωi, is given as 90 rpm.
- The final angular velocity of the disc after the wax sticks to it, ωf, is given as 60 rpm.
To apply the conservation of angular momentum, we need to convert the angular velocities from revolutions per minute (rpm) to radians per second (rad/s).
According to the conservation of angular momentum:
- Li is the initial angular momentum.
- Lf is the final angular momentum.
Setting the initial and final angular momentum equal gives us:
Substituting the values of ωi and ωf:
Expanding the right side:
Calculating 9.42−6.28:
The moment of inertia of the disc is:
Similar Questions
A horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis if the number of revolution per minute is thereby reduced to 90. Calculate the moment of inertia of disc.
View SolutionA horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis if the number of revolution per minute is thereby reduced to 90. Calculate the moment of inertia of disc.
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionAn uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upwards, then about the fixed axis.
STATEMENT-1 : Angular speed of the disc about the aixs of rotation will increase.
and
STATEMENT-2 : Moment of inertia of the disc is decreased about the axis of rotation.
View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View Solution(A) : Moment of inertia of a particle changes with axis of rotation.
(R ) : Moment of inertia depends on mass and distance of the particle from the axis of rotation.
View SolutionA disc rotates about its axis with a constant angular acceleration of 4rads2. Find the radial and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
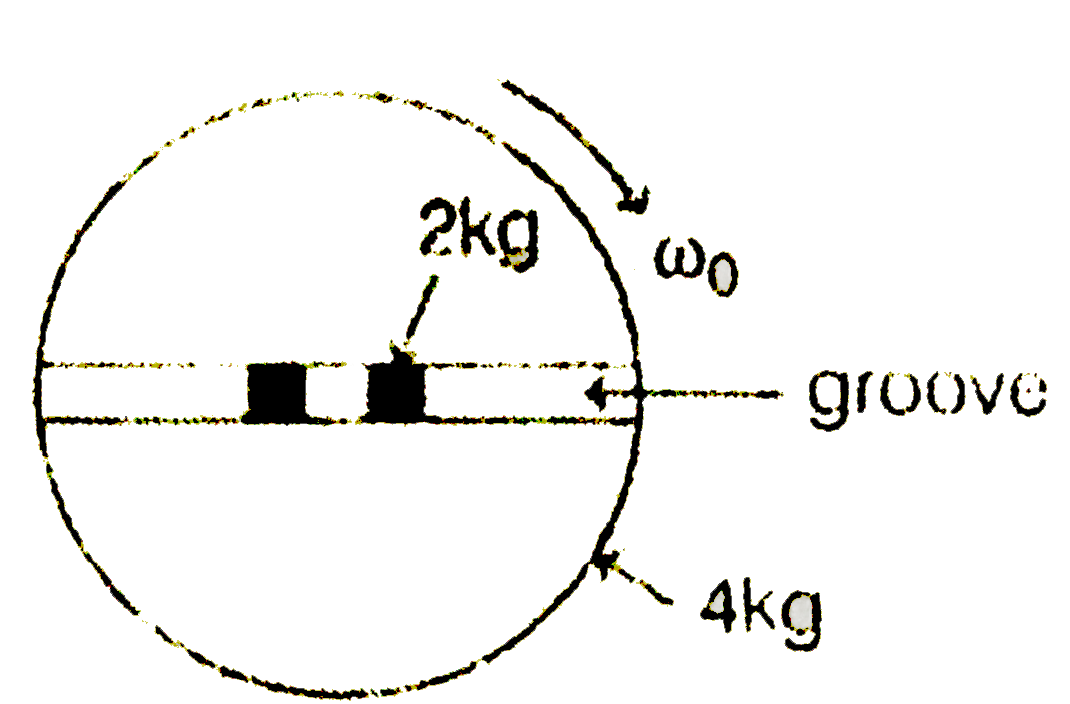
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View Solution
