Two rods of equal lengths(l) and equal mass M are kept along x and y axis respectively such that their centre of mass lie at origin. The moment of inertia about an line y = x, is
ml23
ml24
ml212
ml26
The correct Answer is:C
To find the moment of inertia of the two rods about the line y=x, we can follow these steps:
Step 1: Understand the Configuration
We have two rods of equal length l and equal mass M. One rod is aligned along the x-axis and the other along the y-axis. Their centers of mass are at the origin (0,0).
Step 2: Identify the Angle
The line y=x makes an angle of 45∘ with both the x-axis and y-axis.
Step 3: Moment of Inertia Formula
The moment of inertia I of a rod about an axis passing through its center of mass and making an angle θ with the rod is given by:
I=ML212sin2θ
where L is the length of the rod.
Step 4: Calculate Moment of Inertia for Each Rod
1. For the rod along the x-axis:
- The angle θ=45∘.
- Thus, the moment of inertia I1 is:
I1=ML212sin2(45∘)=ML212⋅(1√2)2=ML212⋅12=ML224
2. For the rod along the y-axis:
- The angle θ=45∘ is the same.
- Thus, the moment of inertia I2 is:
I2=ML212sin2(45∘)=ML212⋅(1√2)2=ML212⋅12=ML224
Step 5: Total Moment of Inertia
Since the moment of inertia is a scalar quantity, we can add the moments of inertia of both rods:
Itotal=I1+I2=ML224+ML224=2ML224=ML212
Final Answer
The moment of inertia of the system about the line y=x is:
ML212
We have two rods of equal length l and equal mass M. One rod is aligned along the x-axis and the other along the y-axis. Their centers of mass are at the origin (0,0).
The line y=x makes an angle of 45∘ with both the x-axis and y-axis.
The moment of inertia I of a rod about an axis passing through its center of mass and making an angle θ with the rod is given by:
I=ML212sin2θ
where L is the length of the rod.
1. For the rod along the x-axis:
- The angle θ=45∘.
- Thus, the moment of inertia I1 is:
I1=ML212sin2(45∘)=ML212⋅(1√2)2=ML212⋅12=ML224
- The angle θ=45∘ is the same.
- Thus, the moment of inertia I2 is:
I2=ML212sin2(45∘)=ML212⋅(1√2)2=ML212⋅12=ML224
Since the moment of inertia is a scalar quantity, we can add the moments of inertia of both rods:
Itotal=I1+I2=ML224+ML224=2ML224=ML212
The moment of inertia of the system about the line y=x is:
ML212
Similar Questions
Three thin rods each of length Land mass M are placed along x, y and z-axes such that one end of each rod is at origin. The moment of inertia of this system about z-axis is
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionIn the diagram shown below all three rods are of equal length L and equal mass M. The system is rotated such that rod B is the axis. What is the moment of inertia of the system ?

View SolutionTwo rods OA and OB of equal length and mass are lying on xy plane as shown in figure. Let Ix,Iy and Iz be the moment of inertia of both the rods bout x,y and z axis respectively. Then,

View SolutionA point object of mass m is kept at (a, 0) along x-axis. What mass should be kept at (-3a,0), so that centre of mass lies at origin ?
View SolutionTwo bodies of masses m and 2m are moving along positive x and y axes respectively with equal speed 4ms−1. They collide at origin and stick together. The final velocity of combined mass is
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
View SolutionThe figure shows an isosceles triangle plate of mass M and base L.
The angle at the apex is 90∘. The apex lies at the origin and the base is parallel to X−axis.
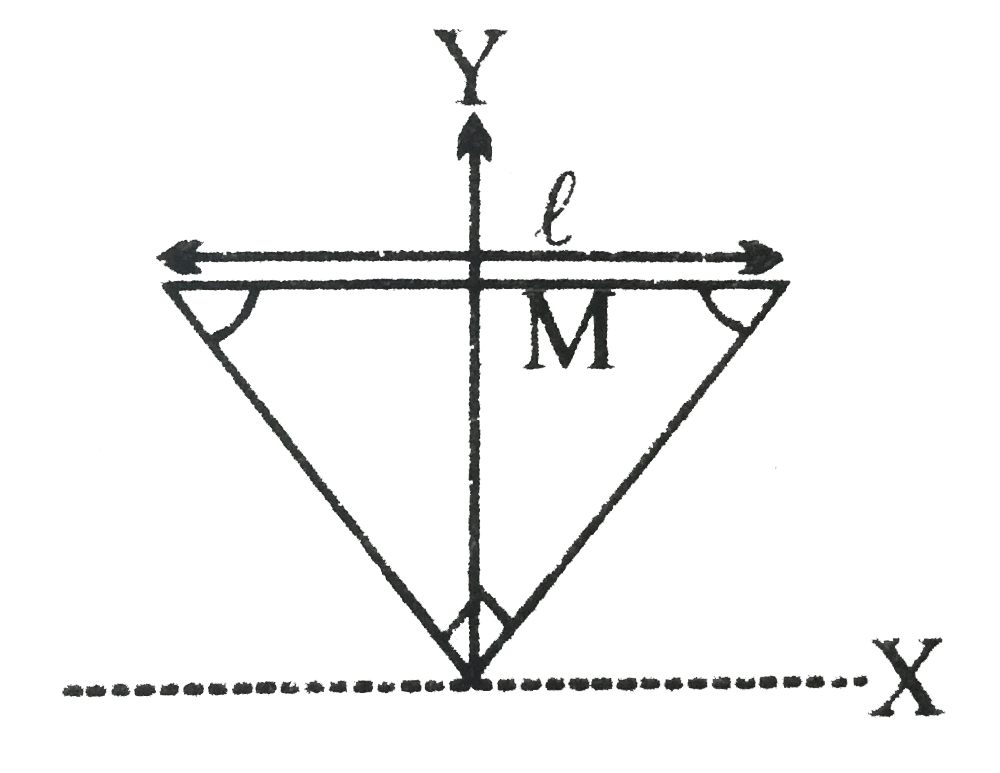
The moment of inertia of the plate about the y−axis is
View SolutionThe figure shows an isosceles triangle plate of mass M and base L.
The angle at the apex is 90∘. The apex lies at the origin and the base is parallel to X−axis.

The moment of inertia of the plate about its base parallel to the x−axis is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View Solution