Two bodies of masses m and 2m are moving along positive x and y axes respectively with equal speed 4ms−1. They collide at origin and stick together. The final velocity of combined mass is
(4ˆi+8ˆj)ms−1
(43ˆi+83ˆj)ms−1
(43ˆi+8ˆj)ms−1
(4ˆi+83ˆj)ms−1
The correct Answer is:c
To solve the problem, we will use the principle of conservation of momentum. Here are the steps to find the final velocity of the combined mass after the collision:
Step 1: Identify the initial velocities of the two masses
- The first body has a mass m and is moving along the positive x-axis with a velocity of 4m/s. Therefore, its velocity vector is:
→v1=4^i
- The second body has a mass 2m and is moving along the positive y-axis with a velocity of 4m/s. Therefore, its velocity vector is:
→v2=4^j
Step 2: Calculate the initial momentum of each body
- The momentum of the first body is given by:
→p1=m⋅→v1=m⋅(4^i)=4m^i
- The momentum of the second body is given by:
→p2=2m⋅→v2=2m⋅(4^j)=8m^j
Step 3: Calculate the total initial momentum before the collision
- The total initial momentum →pinitial is the vector sum of the momenta of both bodies:
→pinitial=→p1+→p2=4m^i+8m^j
Step 4: Determine the total mass after the collision
- After the collision, the two bodies stick together. The total mass M of the combined body is:
M=m+2m=3m
Step 5: Apply conservation of momentum
- According to the conservation of momentum, the total initial momentum is equal to the total final momentum:
→pinitial=→pfinal
- The final momentum can be expressed as:
→pfinal=M⋅→vfinal=3m⋅→vfinal
Step 6: Set up the equation for final velocity
- Equating the total initial momentum to the total final momentum gives us:
4m^i+8m^j=3m⋅→vfinal
- Dividing both sides by 3m (assuming m≠0):
→vfinal=4m^i+8m^j3m=43^i+83^j
Step 7: Conclusion
- The final velocity of the combined mass after the collision is:
→vfinal=43^i+83^jm/s
- The first body has a mass m and is moving along the positive x-axis with a velocity of 4m/s. Therefore, its velocity vector is:
→v1=4^i
- The second body has a mass 2m and is moving along the positive y-axis with a velocity of 4m/s. Therefore, its velocity vector is:
→v2=4^j
- The momentum of the first body is given by:
→p1=m⋅→v1=m⋅(4^i)=4m^i
- The momentum of the second body is given by:
→p2=2m⋅→v2=2m⋅(4^j)=8m^j
- The total initial momentum →pinitial is the vector sum of the momenta of both bodies:
→pinitial=→p1+→p2=4m^i+8m^j
- After the collision, the two bodies stick together. The total mass M of the combined body is:
M=m+2m=3m
- According to the conservation of momentum, the total initial momentum is equal to the total final momentum:
→pinitial=→pfinal
- The final momentum can be expressed as:
→pfinal=M⋅→vfinal=3m⋅→vfinal
- Equating the total initial momentum to the total final momentum gives us:
4m^i+8m^j=3m⋅→vfinal
- Dividing both sides by 3m (assuming m≠0):
→vfinal=4m^i+8m^j3m=43^i+83^j
- The final velocity of the combined mass after the collision is:
→vfinal=43^i+83^jm/s
Topper's Solved these Questions
Similar Questions
Two particles, A and B of masses m and 3m, are moving along X and Y axes respectively, with the same speed v. They collide at the origin, and coalesce into one body, after the c ollision. What is the velocity of this coalesced mass ?
View SolutionTwo masses of 0.25 kg each moves toward each other with speed 3 ms−1 collide and stick together. Find the final velocity
View SolutionTwo bodies of masses m1, and m2, moving with velocity u1, and u2, respectively in the same direction collide with each other elastically. Calculate their velocities after the collision. Discuss what happens when
(i) Both the colliding bodies have the same mass.
(ii) One of the bodies is initially at rest.
(iii) A light body collides with a heavy body at rest
(iv) A heavy body collides with a light body at rest
View SolutionTwo bodies of masses 4kg and 2kg are moving towards each other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionA block at rest explodes into three equal parts. Two parts start moving along X and Y axes respectively with equal speeds of 10 m/s. Find the initial velocity of the third part.
View SolutionTwo particles one of mass m and the other of mass 2 m are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s respectively . They collide in air and stick to each other . The distance from A , where the combined mass finally land is
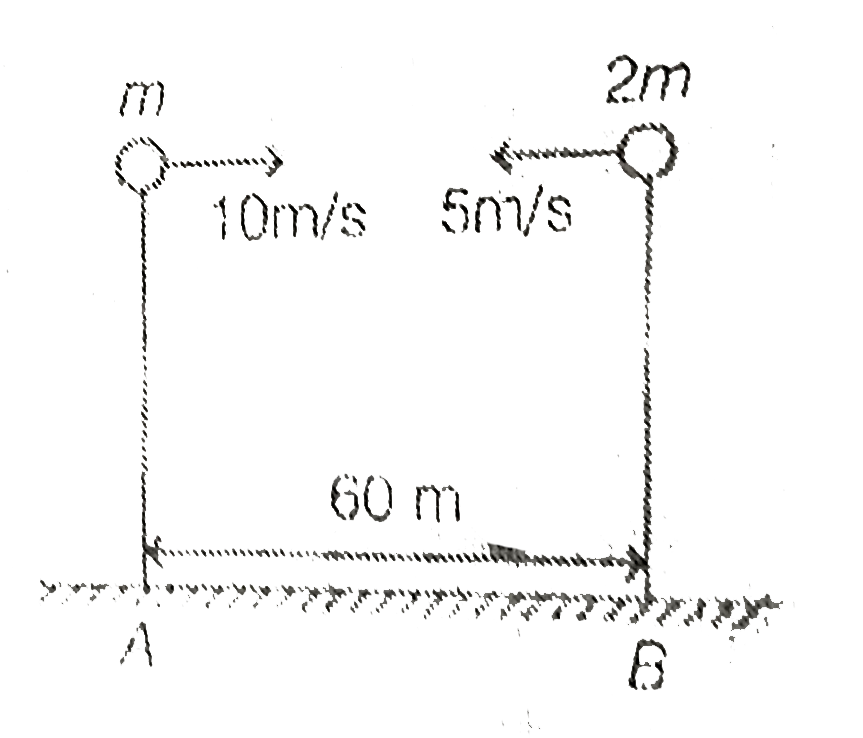
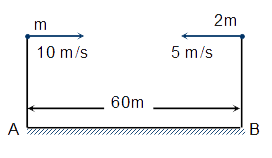
View SolutionTwo particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
View SolutionTwo bodies of masses m and 2m are moving in same direction with speed 2v and v respectively just after collision body of mass m come to rest and body of mass 2m splits in two equal parts and move at 45∘ from initial direction of body of mass m. Find out speed of one part after collision
View SolutionTwo bodies of masses 3 kg and 2 kg are moving towards wach other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View Solution
