The length of a metal wire is when the tensionin it is when the tension is . The natural length of the wire is
The correct Answer is:C
To find the natural length of the metal wire, we can use the relationship between tension, length, and Young's modulus. Here’s a step-by-step solution:
Step 1: Understand the relationship between stress, strain, and Young's modulus
According to Hooke's Law, stress is proportional to strain. The formula for stress (σ) is given by:
σ=TA
where T is the tension and A is the cross-sectional area of the wire. The strain (ε) is defined as:
ϵ=ΔLL0
where ΔL is the change in length and L0 is the original (natural) length of the wire.
Step 2: Write the equations for the two states of the wire
For the first state of the wire (length L1 and tension T1):
Strain1=L1−L0L0
Thus, the Young's modulus Y can be expressed as:
Y=σ1ϵ1=T1AL1−L0L0⟹Y=T1L0A(L1−L0)
For the second state of the wire (length L2 and tension T2):
Strain2=L2−L0L0
Thus, the Young's modulus Y can also be expressed as:
Y=σ2ϵ2=T2AL2−L0L0⟹Y=T2L0A(L2−L0)
Step 3: Set the two expressions for Young's modulus equal
Since the Young's modulus is the same for both states (as the material is the same), we can set the two equations equal to each other:
T1L0L1−L0=T2L0L2−L0
Step 4: Cross-multiply to eliminate fractions
Cross-multiplying gives:
T1L0(L2−L0)=T2L0(L1−L0)
Step 5: Expand and rearrange the equation
Expanding both sides:
T1L0L2−T1L20=T2L0L1−T2L20
Rearranging gives:
T1L0L2−T2L0L1=T1L20−T2L20
Step 6: Factor out L0
Factoring out L0 from the right side:
T1L0L2−T2L0L1=L0(T1−T2)
Step 7: Solve for the natural length L0
Rearranging gives:
L0(T1−T2)=T1L2−T2L1
Thus, we can solve for L0:
L0=T1L2−T2L1T1−T2
Final Answer:
The natural length of the wire is:
L0=T1L2−T2L1T1−T2
According to Hooke's Law, stress is proportional to strain. The formula for stress (σ) is given by:
σ=TA
where T is the tension and A is the cross-sectional area of the wire. The strain (ε) is defined as:
ϵ=ΔLL0
where ΔL is the change in length and L0 is the original (natural) length of the wire.
For the first state of the wire (length L1 and tension T1):
Strain1=L1−L0L0
Thus, the Young's modulus Y can be expressed as:
Y=σ1ϵ1=T1AL1−L0L0⟹Y=T1L0A(L1−L0)
Strain2=L2−L0L0
Thus, the Young's modulus Y can also be expressed as:
Y=σ2ϵ2=T2AL2−L0L0⟹Y=T2L0A(L2−L0)
Since the Young's modulus is the same for both states (as the material is the same), we can set the two equations equal to each other:
T1L0L1−L0=T2L0L2−L0
Cross-multiplying gives:
T1L0(L2−L0)=T2L0(L1−L0)
Expanding both sides:
T1L0L2−T1L20=T2L0L1−T2L20
Rearranging gives:
T1L0L2−T2L0L1=T1L20−T2L20
Factoring out L0 from the right side:
T1L0L2−T2L0L1=L0(T1−T2)
Rearranging gives:
L0(T1−T2)=T1L2−T2L1
Thus, we can solve for L0:
L0=T1L2−T2L1T1−T2
The natural length of the wire is:
L0=T1L2−T2L1T1−T2
Similar Questions
Knowledge Check
The length of a rubber cord is l1 m when the tension is 4 N and l2 m when the tension is 6 N.The length when the tension is 9 N, is
A(2.5l2−1.5l1)mB(6l2−1.5l1)mC(3l1−l2)mD(3.5l2=−2.5l1)m
The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View SolutionThe length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
View SolutionThe length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
View SolutionWhen the tension in a metal wire is T1, its length is I1. When the tension is T2, its length is I2. The natural length of wire is
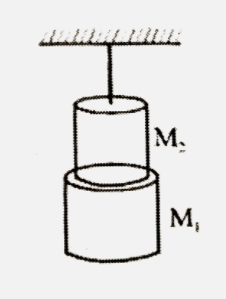
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
View Solutionan elastic spring has a length l1 when tension in it is 4N. Its length is l2 when tension in it is 5N. What will be its length when tension in it is 9N?
View SolutionA transverse wave travels on a taut steel wire with a velocity of when tension in it is 2.06×104N . When the tension is changed to T, the velocity changed to 3v. The value of T is close to :
View Solution
