A uniform cube is subjected to volume compression. If each side is decreased by 2% , then bulk strain is
0.03
0.02
0.06
0.12
To find the bulk strain when a uniform cube is subjected to volume compression and each side is decreased by 2%, we can follow these steps:
Step 1: Understand the relationship between volume and side length
The volume V of a cube is given by the formula:
V=L3
where L is the length of one side of the cube.
Step 2: Determine the change in side length
If each side of the cube is decreased by 2%, the new length L′ can be expressed as:
L′=L−0.02L=0.98L
Step 3: Calculate the new volume
The new volume V′ after the decrease in side length is:
V′=(L′)3=(0.98L)3=0.983L3
Step 4: Calculate the change in volume
The change in volume ΔV is given by:
ΔV=V′−V=0.983L3−L3
Factoring out L3:
ΔV=L3(0.983−1)
Step 5: Calculate the percentage change in volume
The original volume V is L3, so the percentage change in volume is:
Percentage change in volume=ΔVV×100=L3(0.983−1)L3×100=(0.983−1)×100
Step 6: Calculate 0.983
Calculating 0.983:
0.983≈0.941192
Thus,
0.983−1≈0.941192−1=−0.058808
Step 7: Calculate the percentage change
Now, substituting back:
Percentage change in volume=−0.058808×100≈−5.88%
Step 8: Relate to bulk strain
The bulk strain ϵb is defined as:
ϵb=−ΔVV
From our calculations, we have:
ϵb≈0.0588
Final Result
Thus, the bulk strain is approximately 0.0588 or 5.88%.
The volume V of a cube is given by the formula:
V=L3
where L is the length of one side of the cube.
If each side of the cube is decreased by 2%, the new length L′ can be expressed as:
L′=L−0.02L=0.98L
The new volume V′ after the decrease in side length is:
V′=(L′)3=(0.98L)3=0.983L3
The change in volume ΔV is given by:
ΔV=V′−V=0.983L3−L3
Factoring out L3:
ΔV=L3(0.983−1)
The original volume V is L3, so the percentage change in volume is:
Percentage change in volume=ΔVV×100=L3(0.983−1)L3×100=(0.983−1)×100
Calculating 0.983:
0.983≈0.941192
Thus,
0.983−1≈0.941192−1=−0.058808
Now, substituting back:
Percentage change in volume=−0.058808×100≈−5.88%
The bulk strain ϵb is defined as:
ϵb=−ΔVV
From our calculations, we have:
ϵb≈0.0588
Thus, the bulk strain is approximately 0.0588 or 5.88%.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-B)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-C)
29 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
Knowledge Check
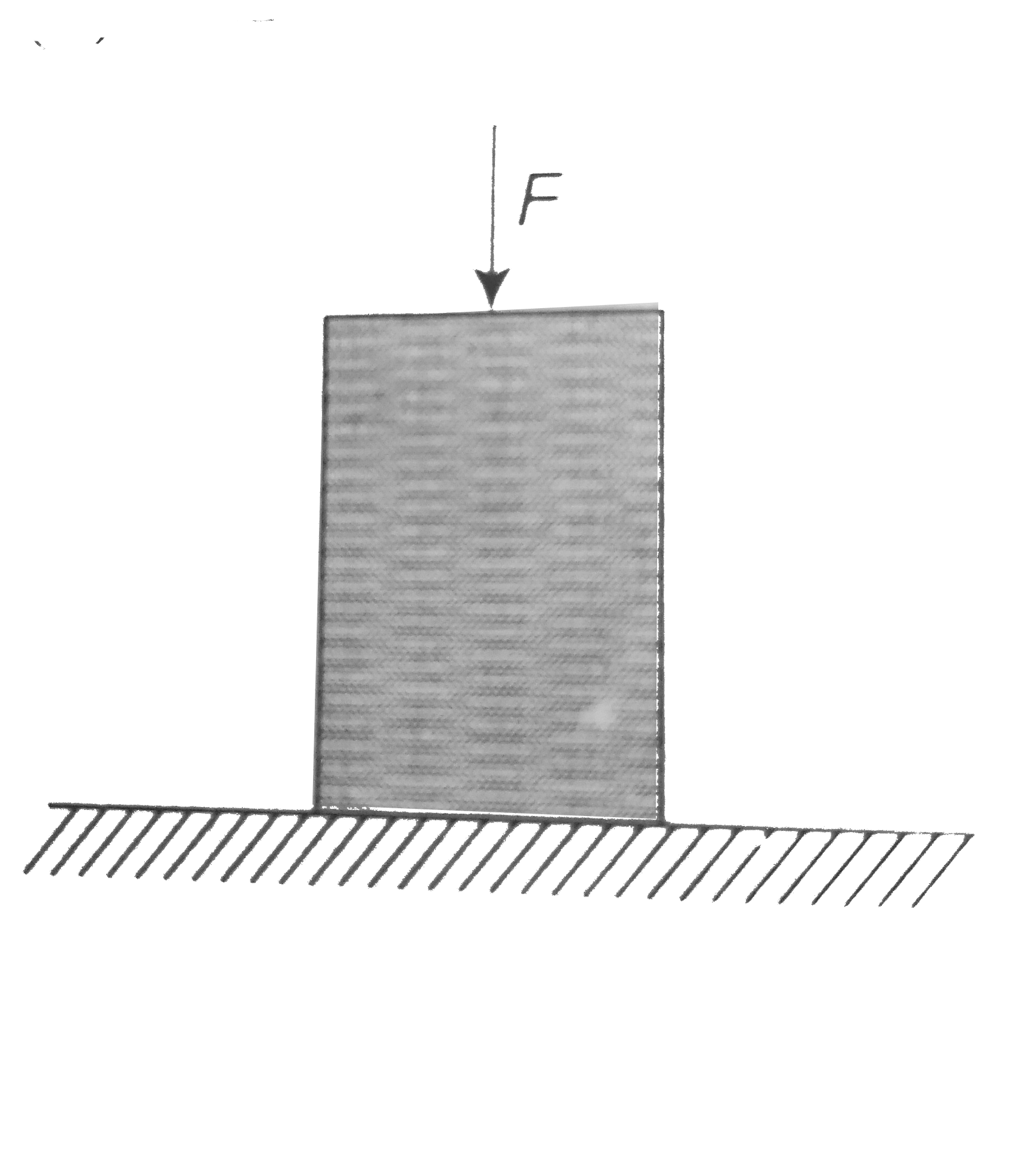
A metal cylinder of length L is subjected to a uniform compressive to a uniform compressive force F as shown in the figure. The material of the cylinder has Young's modulus Y and poisson's ratio σ The change in volume of the cylinder isAsigamFLYB(1−σ)FLYC(1+2σ)FLYD(1−2σ)FLY
When a liquid is subjected to a 15 atmospheric pressure, then its volume decreases by 0.1%. Then bulk modulus of elasticity (K) of the liquid is (1 atm pressure = 105N/m2)
View SolutionThe bulk modulus of a spericla object is B. If it is subjected to uniform pressure p, the fractional decrease in radius is
View SolutionThe bulk modulus of a spherical object is B if it is subjected to uniform pressure p, the fractional decrease in radius is:
View SolutionIf the length of a seconds pendulum is decreased by 2% find the gain or loss per day.
View SolutionIf a simple pendulum is taken to place where g decreases by 2%, then the time period
View SolutionIf the length of second's pendulum is decreased by 2%, how many seconds it will lose per day
View SolutionWhen a rubber ball is taken to the bottom of a sea of depth 1400m the volume decreases by 2%. The Bulk modulus of rubber ball is (density of water is 1g/cm3 and g=10m/s2
View Solution
