When a liquid is subjected to a 15 atmospheric pressure, then its volume decreases by 0.1%. Then bulk modulus of elasticity (K) of the liquid is (1 atm pressure = 105N/m2)
1.5×1010N/m2
1.4×108N/m2
1.5×109N/m2
1.4×109N/m2
The correct Answer is:D
To find the bulk modulus of elasticity (K) of the liquid when it is subjected to a pressure of 15 atmospheres and its volume decreases by 0.1%, we can follow these steps:
Step 1: Understand the given data
- The pressure applied (P) = 15 atm
- The volume change (ΔV) = 0.1% of the original volume (V)
Step 2: Convert the percentage change in volume to a decimal
The change in volume can be expressed as:
ΔV=0.1% of V=0.1100×V=0.001V
Step 3: Calculate the volumetric strain
Volumetric strain (ε) is defined as the change in volume (ΔV) divided by the original volume (V):
ϵ=ΔVV=0.001VV=0.001
Step 4: Calculate the change in pressure (ΔP)
The change in pressure (ΔP) is the difference between the final pressure and the initial pressure. Since the initial pressure is atmospheric pressure (1 atm), we have:
ΔP=P−Pinitial=15 atm−1 atm=14 atm
Step 5: Convert ΔP from atmospheres to N/m²
Using the conversion factor 1 atm=105 N/m2:
ΔP=14 atm×105 N/m2/atm=1.4×106 N/m2
Step 6: Calculate the bulk modulus (K)
The bulk modulus (K) is defined as the ratio of the change in pressure (ΔP) to the volumetric strain (ε):
K=ΔPϵ=1.4×106 N/m20.001=1.4×109 N/m2
Conclusion
The bulk modulus of elasticity (K) of the liquid is:
K=1.4×109 N/m2
- The pressure applied (P) = 15 atm
- The volume change (ΔV) = 0.1% of the original volume (V)
The change in volume can be expressed as:
ΔV=0.1% of V=0.1100×V=0.001V
Volumetric strain (ε) is defined as the change in volume (ΔV) divided by the original volume (V):
ϵ=ΔVV=0.001VV=0.001
The change in pressure (ΔP) is the difference between the final pressure and the initial pressure. Since the initial pressure is atmospheric pressure (1 atm), we have:
ΔP=P−Pinitial=15 atm−1 atm=14 atm
Using the conversion factor 1 atm=105 N/m2:
ΔP=14 atm×105 N/m2/atm=1.4×106 N/m2
The bulk modulus (K) is defined as the ratio of the change in pressure (ΔP) to the volumetric strain (ε):
K=ΔPϵ=1.4×106 N/m20.001=1.4×109 N/m2
The bulk modulus of elasticity (K) of the liquid is:
K=1.4×109 N/m2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - C
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - D
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
When a pressure of 100 atmosphere is applied on a spherical ball, then its volume reduces to 0.01%. The bulk modulus of the material of the rubber in dyne/cm2 is
View SolutionA spherical ball contracts in volume by 0.02% when subjected to a normal uniform pressure of 200 atmospheres. Then Bulk modulus (in N/m2) of the material of the ball is
(Atomospheric pressure =105N/m2)
View Solution
Knowledge Check
A glass slab is subjected to a pressure of 10 atm. The fractional change in its volume is
(Bulk modalus of glass =37×109Nm−2,1atm=1×105Nm−2)A2.7×10−2B2.7×10−3C2.7×10−4D2.7×10−5
An cube is shifted to a depth of 100m is a lake. The change in volume is 0.1%. The bulk modulus of the material is
View SolutionHow much should the pressure on a litre of water be changed to compress it by 0.10%? Bulk modulus of elasticity of water = 2.2×109Nm−2.
View SolutionWhen a rubber ball is taken to the bottom of a sea of depth 1400m the volume decreases by 2%. The Bulk modulus of rubber ball is (density of water is 1g/cm3 and g=10m/s2
View SolutionA monometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas A'asfollows<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NRA_PHY_CHM_JMA_C03_E01_213_Q01.pngwh=80%sty≤=background:white;><br>Ifthesameliqusused∈¯ometer→measuretheatmosphericpressure,thenwˆwillbethe≤n>hoftheliquolumn,whichexertspressureequal→1atm?(densityofHg=13.6g//cm^(3))
View Solution50L of a certain liquid is confined in a piston system at the external pressure 100atm. This pressure is suddenly released and liquid is expanded against the constant atmospheric pressure, volume of the liquid increases by 1L and the final pressure on the liquid is 10atm. Find the workdone.
View SolutionA manometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas 'A' as follows
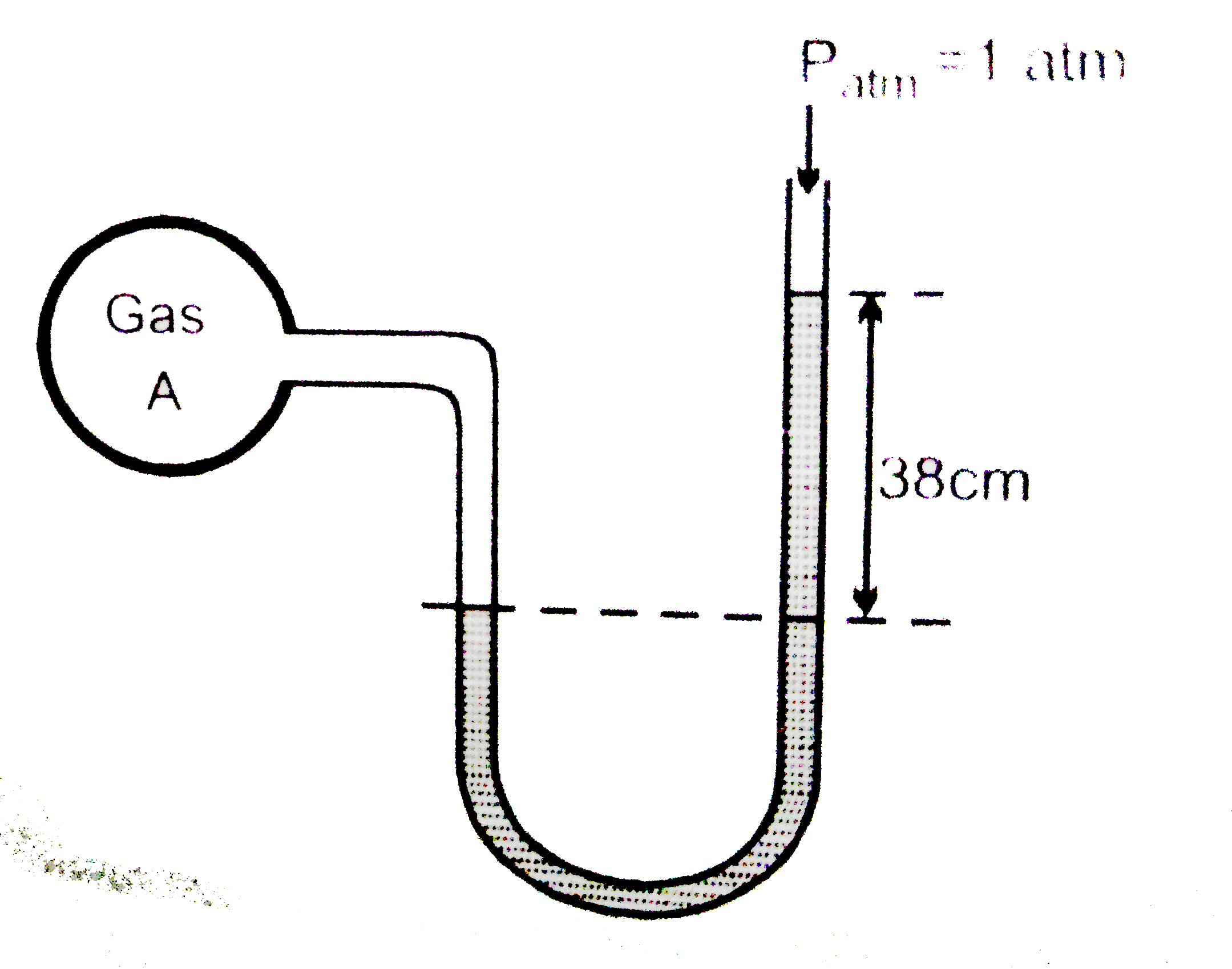
If the same liquid is used in barometer to measure the atmospheric pressure, then what will be the lengh of the liquid columnm which exerts pressure equal to 1 atm ? (density of Hg=13.6g/cm3)
View SolutionCompute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atmosphere. Bulk modulus of elasticity of glass = 37×109Nm−2 and 1 atm = 1.013×105Pa.
View Solution
