Three bars having length l,2land3l and of cross-section A, 2A and 3A are joined
rigidly end to end Compound rod is subjected to a stretching force F . The increase in length of rod is (Young's
modules of material is Y, and bars are massless)
(A) 13Fl2AY
(B)
FlAY
(C) 9FlAY
(D) 3FlAY
13Fl2AY
FlAY
9FlAY
3FlAY
To solve the problem, we need to calculate the total increase in length of a compound rod made up of three bars with different lengths and cross-sectional areas when subjected to a stretching force F.
1. Identify the Parameters:
- Lengths of the bars: L1=l, L2=2l, L3=3l
- Cross-sectional areas of the bars: A1=A, A2=2A, A3=3A
- Young's modulus of the material: Y
- Stretching force: F
2. Understand the Relationship:
- The increase in length (extension) ΔL of each bar can be calculated using the formula:
ΔL=F⋅LA⋅Y
- Since the bars are connected in series, the total extension ΔLtotal is the sum of the extensions of each bar:
ΔLtotal=ΔL1+ΔL2+ΔL3
3. Calculate the Extension for Each Bar:
- For the first bar (length l, area A):
ΔL1=F⋅lA⋅Y
- For the second bar (length 2l, area 2A):
ΔL2=F⋅(2l)(2A)⋅Y=F⋅lA⋅Y
- For the third bar (length 3l, area 3A):
ΔL3=F⋅(3l)(3A)⋅Y=F⋅lA⋅Y
4. Combine the Extensions:
- Now, add the extensions:
ΔLtotal=ΔL1+ΔL2+ΔL3=F⋅lA⋅Y+F⋅lA⋅Y+F⋅lA⋅Y
- This simplifies to:
ΔLtotal=3⋅F⋅lA⋅Y=3F⋅lA⋅Y
5. Final Result:
- Therefore, the total increase in length of the compound rod is:
ΔLtotal=3FlAY
Conclusion:
The correct answer is (D) 3FlAY.
- Lengths of the bars: L1=l, L2=2l, L3=3l
- Cross-sectional areas of the bars: A1=A, A2=2A, A3=3A
- Young's modulus of the material: Y
- Stretching force: F
- The increase in length (extension) ΔL of each bar can be calculated using the formula:
ΔL=F⋅LA⋅Y
- Since the bars are connected in series, the total extension ΔLtotal is the sum of the extensions of each bar:
ΔLtotal=ΔL1+ΔL2+ΔL3
- For the first bar (length l, area A):
ΔL1=F⋅lA⋅Y
- For the second bar (length 2l, area 2A):
ΔL2=F⋅(2l)(2A)⋅Y=F⋅lA⋅Y
- For the third bar (length 3l, area 3A):
ΔL3=F⋅(3l)(3A)⋅Y=F⋅lA⋅Y
- Now, add the extensions:
ΔLtotal=ΔL1+ΔL2+ΔL3=F⋅lA⋅Y+F⋅lA⋅Y+F⋅lA⋅Y
- This simplifies to:
ΔLtotal=3⋅F⋅lA⋅Y=3F⋅lA⋅Y
- Therefore, the total increase in length of the compound rod is:
ΔLtotal=3FlAY
The correct answer is (D) 3FlAY.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-C)
29 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-A)
54 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
If a wire of length 4 m and cross-sectional area of 2m2 is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is 110×109Nm−2
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
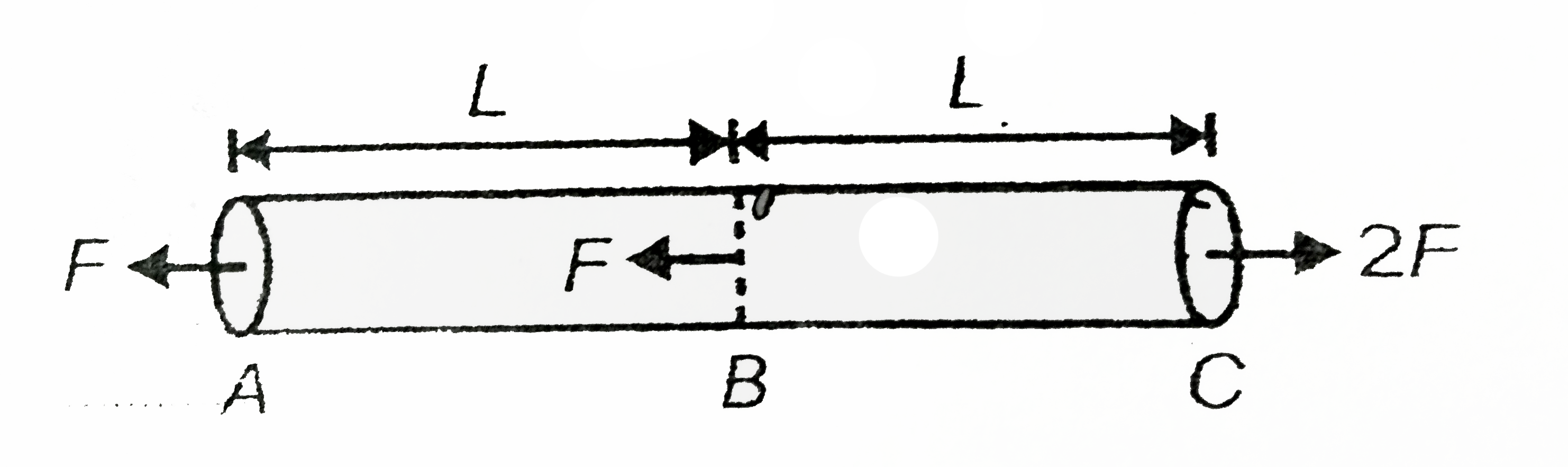
Select the correct alternatives.
View Solution
Knowledge Check
A wire of length L and radius r is clamped at one end. On stretching the other end of the wire with a force F, the increase in its length is 1. If another wire of same material but of length 2L and radius 2r is stretched with a force 2F, the increase in its leagth will be
Al4Bl2ClD2l
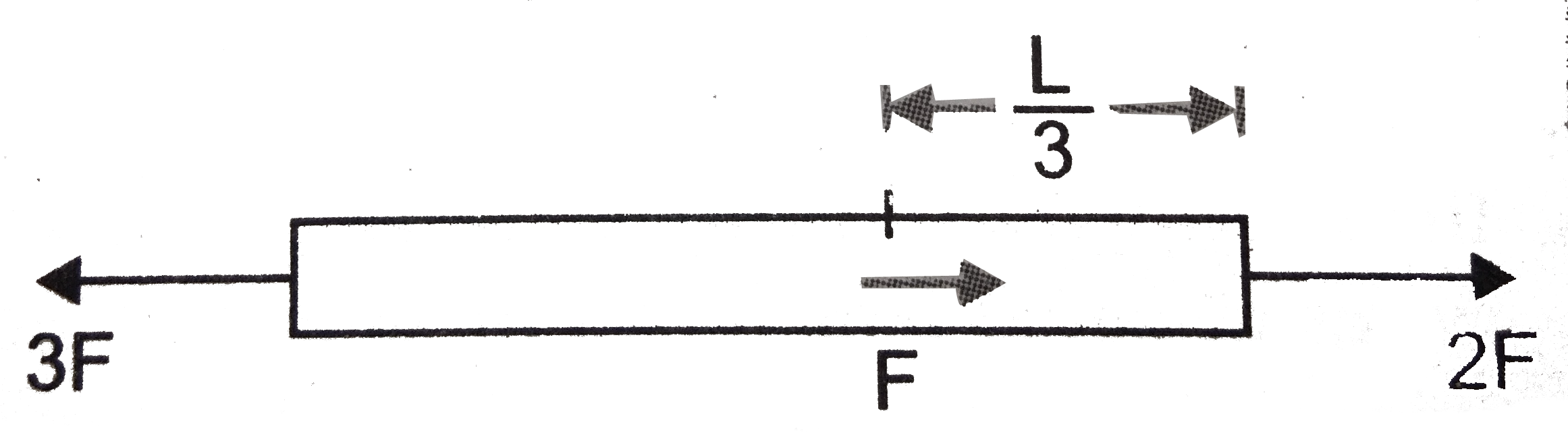
A uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View SolutionA rod of mass, m uniform corss sectional area A and length L is accelerated by applying force F as shown in figure on a smooth surface. If yougs' modulus of elasticity of the material of rod is Y. (Consider x as measured from the right end).

View SolutionA wire havinga length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the vqalue of α
View SolutionA rod of length l and radius r is joined to a rod of length l/2 and radius r/2 of same material. The free end of small rod is fixed to a rigid base and the free end of larger rod is given a twist of θ∘, the twist angle at the joint will be
View SolutionA steel rod has a radius of cross-sectional area is R= 10 mm and length L = 90 cm ls fixed at one end, a force F=3.14⋅104N stretches it along its length, the stress in the rod is equal to (take π = 3.14)
View SolutionIf two wires of same length l and are of the cross-section A with young modulus Y and 2Y connect in series and one end is fixed on roof and another end with mass m makes simple harmonic motion, then the time period is
View SolutionA wire of length L and radius a rigidlyl fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is L, if another wire of same material but of length 2 L and radius 2 a is stretched with a force 2 F, the increase in its length will be
View Solution
