The strain energy stored in a body of volume V due to shear strain is ϕ (shear modulus is n)
ϕ2V2n
ϕV22n
ϕ2Vn
12nϕ2V
To find the strain energy stored in a body of volume V due to shear strain ϕ, where the shear modulus is n, we can follow these steps:
1. Understand the Formula for Strain Energy:
The strain energy U stored in a material due to deformation can be expressed as:
U=12×stress×volume×strain
2. Relate Stress to Shear Modulus:
The shear stress τ in terms of shear modulus n and shear strain ϕ is given by:
τ=n⋅ϕ
3. Substitute Stress into the Strain Energy Formula:
Now, substituting the expression for shear stress into the strain energy formula, we have:
U=12×(n⋅ϕ)×V×ϕ
4. Simplify the Expression:
This simplifies to:
U=12×n×V×ϕ2
5. Final Expression for Strain Energy:
Thus, the strain energy stored in the body can be expressed as:
U=nVϕ22
Conclusion:
The strain energy stored in a body of volume V due to shear strain ϕ is given by:
U=nVϕ22
The strain energy U stored in a material due to deformation can be expressed as:
U=12×stress×volume×strain
The shear stress τ in terms of shear modulus n and shear strain ϕ is given by:
τ=n⋅ϕ
Now, substituting the expression for shear stress into the strain energy formula, we have:
U=12×(n⋅ϕ)×V×ϕ
This simplifies to:
U=12×n×V×ϕ2
Thus, the strain energy stored in the body can be expressed as:
U=nVϕ22
The strain energy stored in a body of volume V due to shear strain ϕ is given by:
U=nVϕ22
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-C)
29 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-A)
54 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
Knowledge Check
The shear modulus is also known as
AÂ bulk modulusBYoung's modulusCmodulus of rigicityDPossion's ratioThe ratio of shearing stress to the shearing strain is defined as
AYoung's modulusBbulk modulusCshear modulusDcompressibility
The elastic energy per unit volume is terms of longitudinal strain σ and Young's modulus Y is
View SolutionThe stored energy per unit volume of a stretched wire is
View SolutionA 0.05m cube has its upper face displaced by 0.2cm by a tangential force of 8N. Calculate the shearing strain, shearing stress and modulus of rigidity of the material of the cube.
View SolutionHow should we apply a force on a body to produce shearing stress?
View SolutionDefine strain energy. Write formula for the same
View Solution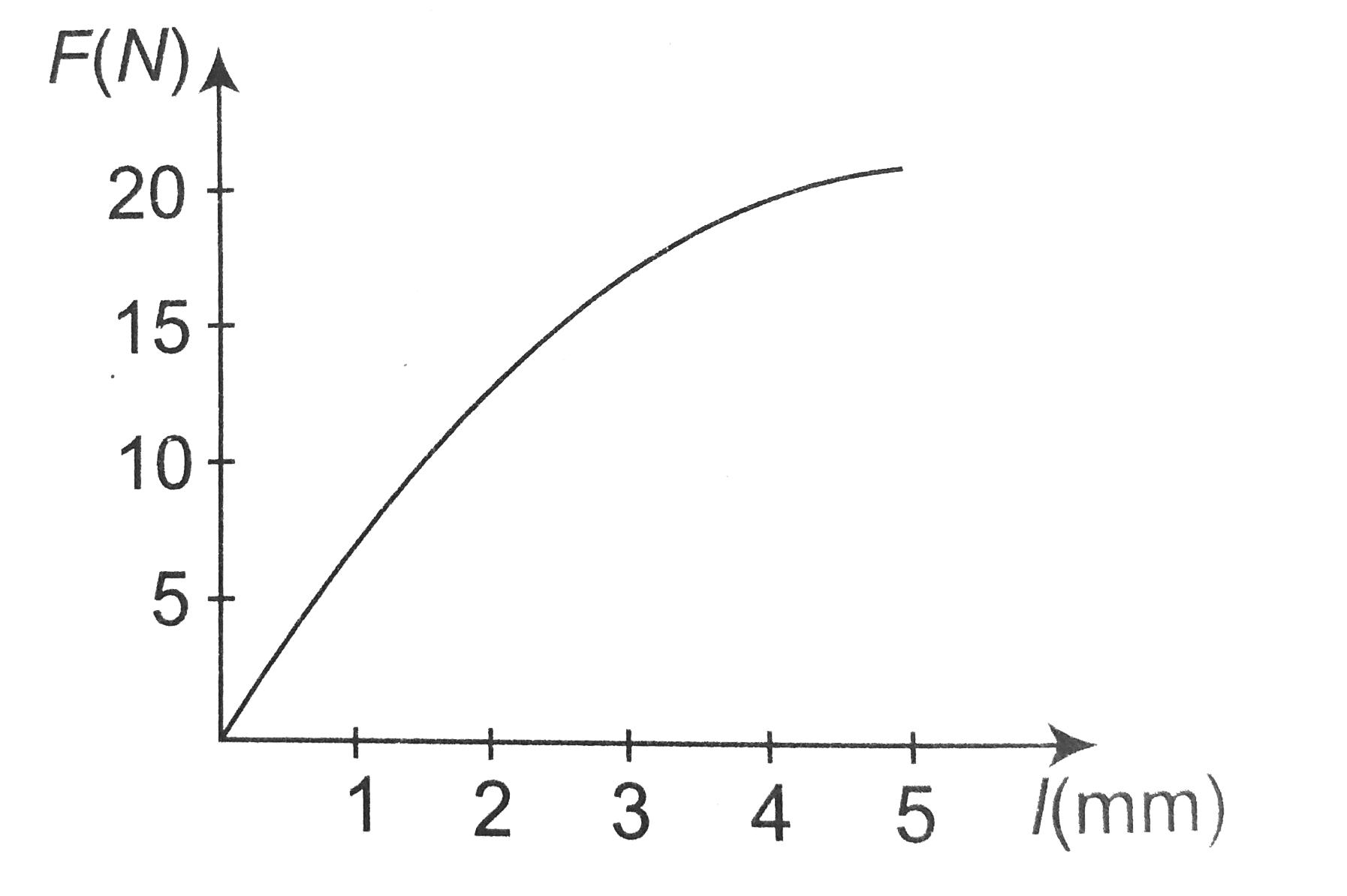
The force (F)- extension (λ) graph shows that the strain energy stored in the material under test, for an extension of 4mm, is greater than which of the following values?
View Solution
