A : Gravitational potential is constant everywhere inside a spherical shell .
R : Gravitational field inside a spherical shell is zero everywhere .
If both Assertion & Reason are true . And the reason is the correct explanation of the assertion , then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion , then mark (2)
If Assertion is true statement but Reason is false , then mark (3)
If Assertion is false statement but Reason is true , then mark (4)
The correct Answer is:A
To solve the given question, we need to analyze the statements A and R regarding gravitational potential and gravitational field inside a spherical shell.
1. Understanding the Statements:
- Statement A: "Gravitational potential is constant everywhere inside a spherical shell."
- Statement R: "Gravitational field inside a spherical shell is zero everywhere."
2. Analyzing Statement R:
- The gravitational field inside a spherical shell is indeed zero everywhere. This can be understood using the principle of superposition.
- Consider a spherical shell with uniform mass distribution. The gravitational field at any point inside the shell is the vector sum of the gravitational fields due to all the mass elements of the shell.
- Due to symmetry, the gravitational forces from different parts of the shell cancel each other out, resulting in a net gravitational field of zero.
3. Analyzing Statement A:
- Gravitational potential (V) is related to the gravitational field (E) by the equation:
E=−dVdr
- Since we established that the gravitational field (E) inside the shell is zero, we can substitute this into the equation:
0=−dVdr
- This implies that the derivative of the gravitational potential with respect to radius is zero, meaning that V must be constant throughout the region inside the shell.
4. Conclusion:
- Both statements A and R are true.
- Statement R correctly explains Statement A, as the zero gravitational field leads to a constant gravitational potential.
Final Answer:
Both A and R are true, and R is the correct explanation of A.
- Statement A: "Gravitational potential is constant everywhere inside a spherical shell."
- Statement R: "Gravitational field inside a spherical shell is zero everywhere."
- The gravitational field inside a spherical shell is indeed zero everywhere. This can be understood using the principle of superposition.
- Consider a spherical shell with uniform mass distribution. The gravitational field at any point inside the shell is the vector sum of the gravitational fields due to all the mass elements of the shell.
- Due to symmetry, the gravitational forces from different parts of the shell cancel each other out, resulting in a net gravitational field of zero.
- Gravitational potential (V) is related to the gravitational field (E) by the equation:
E=−dVdr
- Since we established that the gravitational field (E) inside the shell is zero, we can substitute this into the equation:
0=−dVdr
- This implies that the derivative of the gravitational potential with respect to radius is zero, meaning that V must be constant throughout the region inside the shell.
- Both statements A and R are true.
- Statement R correctly explains Statement A, as the zero gravitational field leads to a constant gravitational potential.
Both A and R are true, and R is the correct explanation of A.
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
51 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
For a spherical shell
View SolutionInside a uniform spherical shell
View SolutionIntensity of gravitational field inside the hollow spherical shell is
View SolutionA : The gravitational field intensity is zero everywhere inside a uniform spherical shell
R: The net force on a point mass inside a uniform spherical shell is zero everywhere .
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
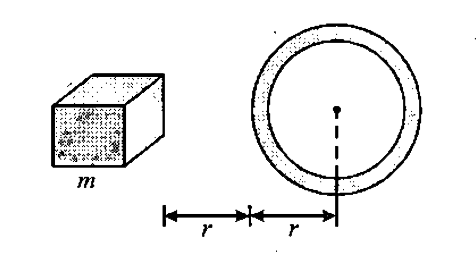
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View SolutionSTATEMENT-1 : Inside an isolated hollow spherical shell of charge, electrostatic potential is constant everywhere
and
STATEMENT-2 : Electric field inside a hollow spherical shell of charge is always zero.
View SolutionIn side a hollow isolated spherical shell-
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionIf gravitational field due to uniform thin hemispherical shell at point P is I, then the magnitude of gravitational field at Q is (Mass of hemispherical shell is M, radius is R)
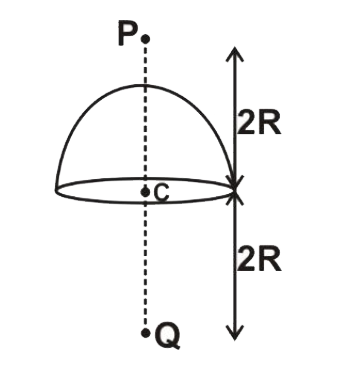
View Solution
