A cube of edge length 10 cm is just balanced at the interface of two liquids A and B as shown in figure. If A and B has specific gravity 0.6 and 0.4 respectively, then mass of cube is
240 g
360 g
480 g
540 g
To find the mass of the cube that is just balanced at the interface of two liquids A and B, we will follow these steps:
Step 1: Understand the Problem
We have a cube with an edge length of 10 cm, which is balanced at the interface of two liquids with specific gravities of 0.6 (liquid A) and 0.4 (liquid B). We need to find the mass of the cube.
Step 2: Convert Edge Length to Meters
The edge length of the cube is given as 10 cm. We convert this to meters for consistency in units:
Edge length=10cm=0.1m
Step 3: Calculate the Volume of the Cube
The volume V of the cube can be calculated using the formula:
V=edge length3=(0.1m)3=0.001m3
Step 4: Determine the Densities of the Liquids
The specific gravity (SG) is the ratio of the density of a substance to the density of water (1000 kg/m³). Therefore, we can find the densities of liquids A and B:
- Density of liquid A (ρA):
ρA=SGA×1000kg/m3=0.6×1000=600kg/m3
- Density of liquid B (ρB):
ρB=SGB×1000kg/m3=0.4×1000=400kg/m3
Step 5: Set Up the Equation for Buoyant Force
The cube is balanced, meaning the weight of the cube is equal to the buoyant force acting on it. The buoyant force FB can be expressed as:
FB=VA⋅ρA⋅g+VB⋅ρB⋅g
where VA and VB are the volumes submerged in liquids A and B, respectively.
Step 6: Determine the Volumes Submerged
Since the cube is balanced at the interface:
- Let hA be the height submerged in liquid A and hB be the height submerged in liquid B.
- For this cube, hA+hB=0.1m.
Assuming the cube is submerged such that:
- hA=0.04m (4 cm in liquid A)
- hB=0.06m (6 cm in liquid B)
The volumes submerged are:
VA=Area×hA=(0.1×0.1)×0.04=0.0004m3
VB=Area×hB=(0.1×0.1)×0.06=0.0006m3
Step 7: Calculate the Buoyant Force
Now we can calculate the buoyant force:
FB=VA⋅ρA⋅g+VB⋅ρB⋅g
Since g cancels out in the equation for mass, we can ignore it for now:
FB=0.0004⋅600+0.0006⋅400
FB=0.24+0.24=0.48N
Step 8: Calculate the Mass of the Cube
Since the weight of the cube mg is equal to the buoyant force:
mg=0.48N
To find the mass m:
m=FBg=0.489.81≈0.0489kg=48.9grams
Step 9: Final Calculation
However, we need to consider the total volume submerged:
m=V⋅ρ=0.001⋅(600⋅0.04+400⋅0.06)
Calculating gives:
m=0.001⋅(24+24)=0.001⋅48=0.048kg=48grams
Conclusion
The mass of the cube is approximately 48grams.
We have a cube with an edge length of 10 cm, which is balanced at the interface of two liquids with specific gravities of 0.6 (liquid A) and 0.4 (liquid B). We need to find the mass of the cube.
The edge length of the cube is given as 10 cm. We convert this to meters for consistency in units:
Edge length=10cm=0.1m
The volume V of the cube can be calculated using the formula:
V=edge length3=(0.1m)3=0.001m3
The specific gravity (SG) is the ratio of the density of a substance to the density of water (1000 kg/m³). Therefore, we can find the densities of liquids A and B:
- Density of liquid A (ρA):
ρA=SGA×1000kg/m3=0.6×1000=600kg/m3
- Density of liquid B (ρB):
ρB=SGB×1000kg/m3=0.4×1000=400kg/m3
The cube is balanced, meaning the weight of the cube is equal to the buoyant force acting on it. The buoyant force FB can be expressed as:
FB=VA⋅ρA⋅g+VB⋅ρB⋅g
where VA and VB are the volumes submerged in liquids A and B, respectively.
Since the cube is balanced at the interface:
- Let hA be the height submerged in liquid A and hB be the height submerged in liquid B.
- For this cube, hA+hB=0.1m.
- hA=0.04m (4 cm in liquid A)
- hB=0.06m (6 cm in liquid B)
VA=Area×hA=(0.1×0.1)×0.04=0.0004m3
VB=Area×hB=(0.1×0.1)×0.06=0.0006m3
Now we can calculate the buoyant force:
FB=VA⋅ρA⋅g+VB⋅ρB⋅g
Since g cancels out in the equation for mass, we can ignore it for now:
FB=0.0004⋅600+0.0006⋅400
FB=0.24+0.24=0.48N
Since the weight of the cube mg is equal to the buoyant force:
mg=0.48N
To find the mass m:
m=FBg=0.489.81≈0.0489kg=48.9grams
However, we need to consider the total volume submerged:
m=V⋅ρ=0.001⋅(600⋅0.04+400⋅0.06)
Calculating gives:
m=0.001⋅(24+24)=0.001⋅48=0.048kg=48grams
The mass of the cube is approximately 48grams.
Similar Questions
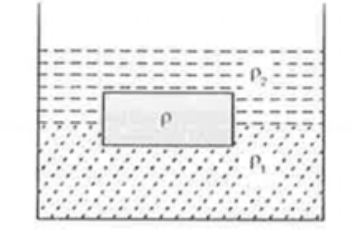
A cube of density p is just balanced at interface of two unmixable liquid A and B having density p1 and p2 respectively as shown, then the fraction of volume of cube in the upper liquid is (p2<p<p1)
View SolutionThe weight of a body at earth's surface is W. At a depth half way to the centre of earth it will weight
View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is

View Solution
A cylinder of mass M and radius R is resting on two corner edges A and B as shown in figure. The normal reaction at the edges A and B are: (Neglect friction)
View Solution
A cylinder of mass M and radius R is resting on two corner edges A and B as shown in figure. The normal reaction at the edges A and B are: (Neglect friction)
View SolutionThe density of a cube is found by measuring its mass and the length of its side of the maximum errors in the measurement of mass and length are 0.3% and 0.2% respectively, the maximum error in the measurement of density is
View SolutionA container contains three liquds as shown in the figure. The specific gravity of liquid 1 and liquid 2 are 0.8 and 1.2 respectively. A small hole having area 10−6m2 at point P is as shown in the figure. Initially hole is closed. The cross-sectional area of container is 50cm2. assume all liquids ae ideal and neglect any type of friction between liquid and container. (Given that g=9.8m/s2 and h=28cm)
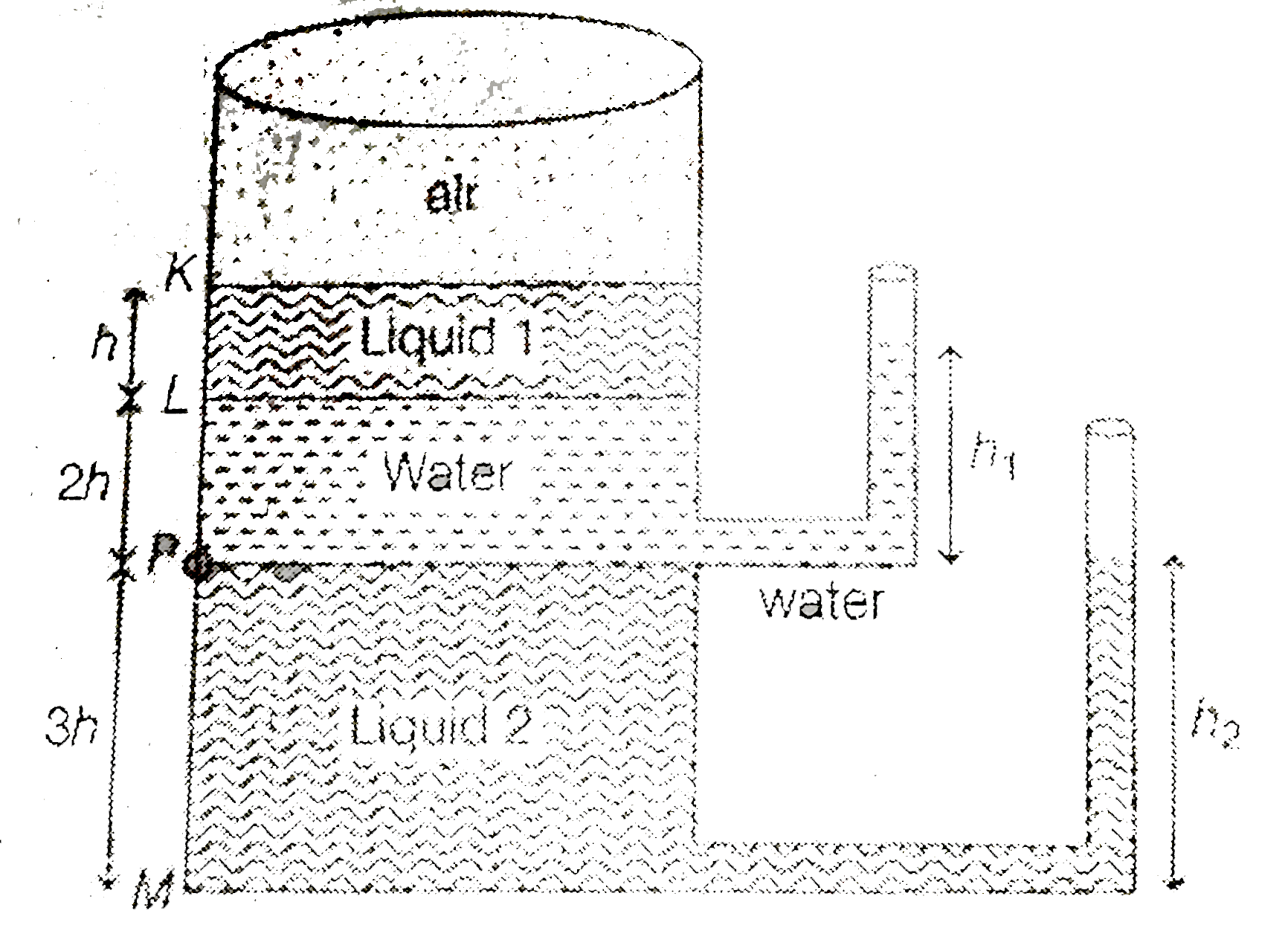
At some instant, hole is opened. the speed of water coming out from hole just after the opening of hole is
View SolutionA solid cylinder of length L is in equilibrium in two different liquid A and B as shown in the figure.The density of liquid A 3ρ2 and liquid B is 3ρ.The density of cylinder is
View SolutionAn ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area 10cm2. The level of kerosene is just covering the top surface of the ice cube.
a. Find the depth of submergence in the kerosene and that in the water.
b. Find the change in the total level of the liquid when the whole ice melts into water.

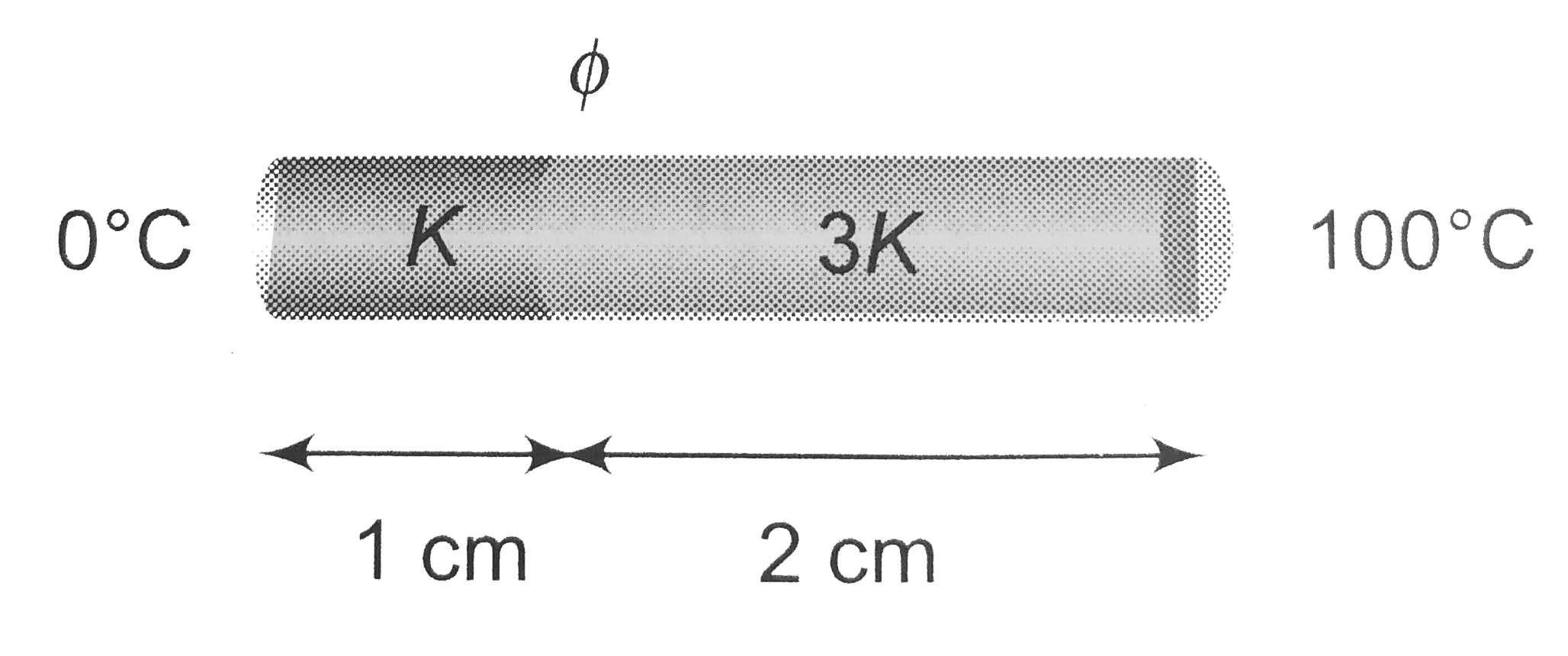
View SolutionTwo bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite br is 0∘C and 100∘C respectively (see figure), then the temperature ϕ of the interface is
View Solution
