A solid cylinder of length L is in equilibrium in two different liquid A and B as shown in the figure.The density of liquid A 3ρ2 and liquid B is 3ρ.The density of cylinder is
7/5ρ
13/5ρ
5/2ρ
2ρ
The correct Answer is:B
To solve the problem of finding the density of the solid cylinder in equilibrium in two different liquids, we can follow these steps:
1. Understanding the Problem: We have a solid cylinder of length L that is in equilibrium in two different liquids, A and B. The density of liquid A is 3ρ2 and the density of liquid B is 3ρ. We need to find the density of the cylinder, denoted as ρC.
2. Weight of the Cylinder: The weight W of the cylinder can be calculated using the formula:
W=m⋅g
where m is the mass of the cylinder and g is the acceleration due to gravity. The mass m can be expressed in terms of density and volume:
m=ρC⋅V
Therefore, the weight can be rewritten as:
W=ρC⋅V⋅g
3. Buoyant Force: The buoyant force B acting on the cylinder is the sum of the buoyant forces from both liquids A and B. The buoyant force can be calculated using the formula:
B=(Density of liquid A)⋅(Volume submerged in liquid A)⋅g+(Density of liquid B)⋅(Volume submerged in liquid B)⋅g
4. Volume Submerged: Let's denote the volume of the cylinder as V. According to the problem, the cylinder is submerged in liquid A for 23 of its volume and in liquid B for 13 of its volume:
- Volume submerged in liquid A: 2V3
- Volume submerged in liquid B: V3
5. Calculating Buoyant Force:
- For liquid A:
BA=(3ρ2)⋅(2V3)⋅g=3ρ2⋅2Vg3=ρVg
- For liquid B:
BB=3ρ⋅(V3)⋅g=ρVg
- Total buoyant force B:
B=BA+BB=ρVg+ρVg=2ρVg
6. Setting Weight Equal to Buoyant Force: For the cylinder to be in equilibrium, the weight must equal the buoyant force:
ρC⋅V⋅g=2ρ⋅V⋅g
7. Cancelling Common Terms: We can cancel V and g from both sides of the equation:
ρC=2ρ
Final Answer:
The density of the cylinder ρC is:
ρC=2ρ
W=m⋅g
where m is the mass of the cylinder and g is the acceleration due to gravity. The mass m can be expressed in terms of density and volume:
m=ρC⋅V
Therefore, the weight can be rewritten as:
W=ρC⋅V⋅g
B=(Density of liquid A)⋅(Volume submerged in liquid A)⋅g+(Density of liquid B)⋅(Volume submerged in liquid B)⋅g
- Volume submerged in liquid A: 2V3
- Volume submerged in liquid B: V3
- For liquid A:
BA=(3ρ2)⋅(2V3)⋅g=3ρ2⋅2Vg3=ρVg
- For liquid B:
BB=3ρ⋅(V3)⋅g=ρVg
- Total buoyant force B:
B=BA+BB=ρVg+ρVg=2ρVg
ρC⋅V⋅g=2ρ⋅V⋅g
ρC=2ρ
The density of the cylinder ρC is:
ρC=2ρ
Similar Questions
A vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
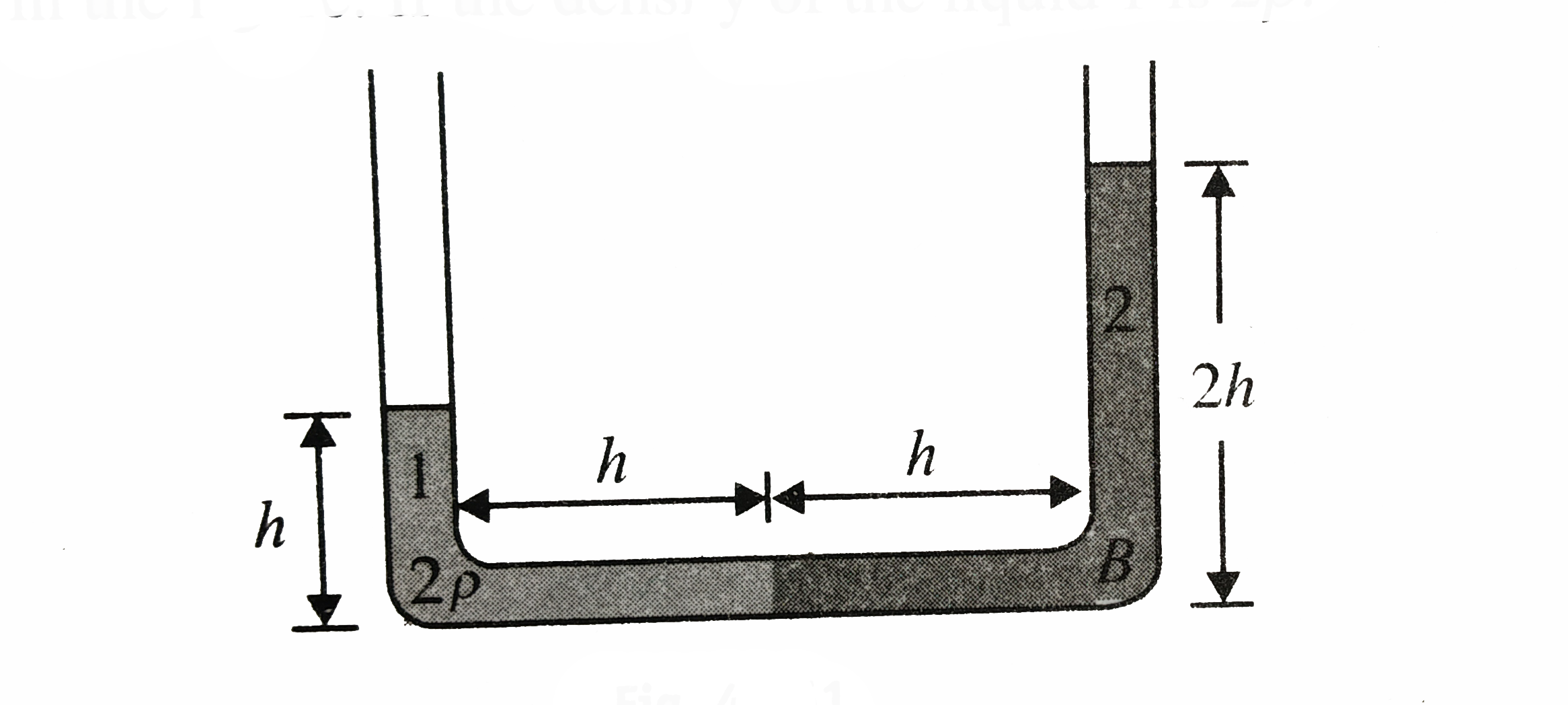
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
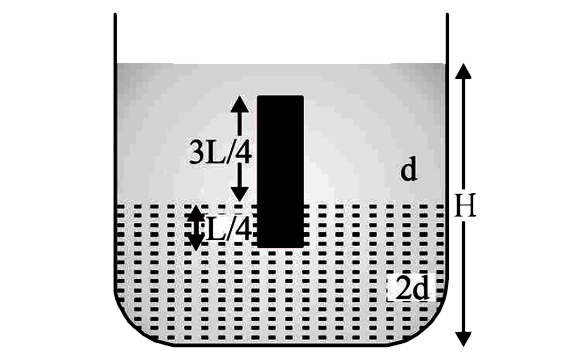
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
View SolutionA cylinder is floating in two liquids as shown in figure. Choose the correct options.
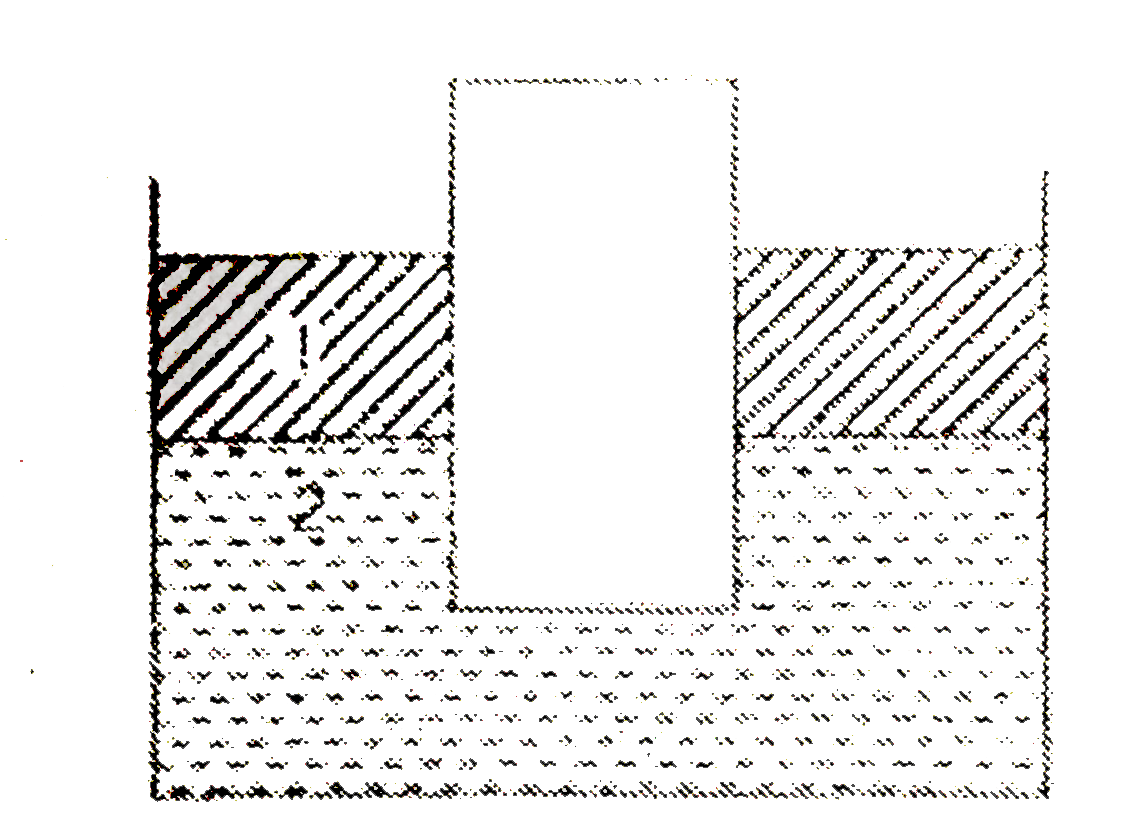
View SolutionTwo non-mixing liquids of densities ρ and nρ (n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to :
View SolutionA vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is

View SolutionA solid 'S'floats in liquid 'L'. The density of 'S' is ……………. than liquid 'L'.
View SolutionMore is the density of a liquid than a solid, more the volume of solid will submerge in it.
View Solution
