A cube of density p is just balanced at interface of two unmixable liquid A and B having density p1 and p2 respectively as shown, then the fraction of volume of cube in the upper liquid is (p2<p<p1)
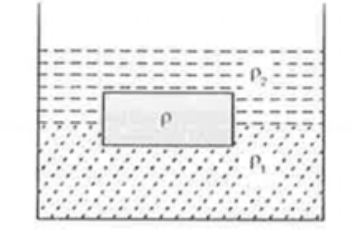
p1−pp1−p2
p1−p2p1+p2
p1−p2p1+p
p1+p2p
The correct Answer is:A
Step by step video & image solution for A cube of density p is just balanced at interface of two unmixable liquid A and B having density p_1 and p_2 respectively as shown, then the fraction of volume of cube in the upper liquid is (p_2 < p < p_1) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
P1 and P2 are respectively :
View SolutionA cube of edge length 10 cm is just balanced at the interface of two liquids A and B as shown in figure. If A and B has specific gravity 0.6 and 0.4 respectively, then mass of cube is
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
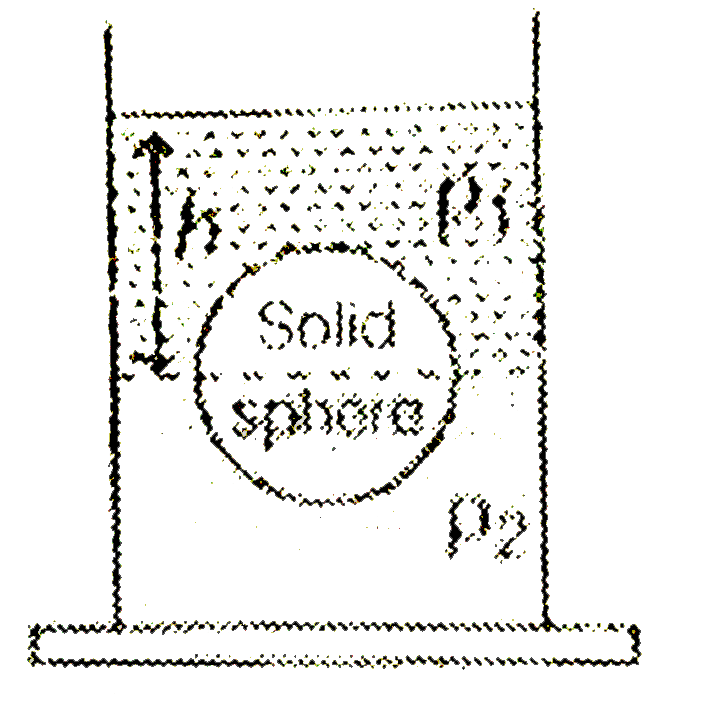
View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the upper liquid is

View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is th especific gracity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is

View SolutionIn the arrangement as shown, A and B arc two cylinders each of length L and density d1 and d2(d1<d2) respectively. They are joined together and submerged in the liquid of density d with length L/2 of A outside the liquid. If the difference in densities of two cylinders is equal to density of the liquid, find d1.
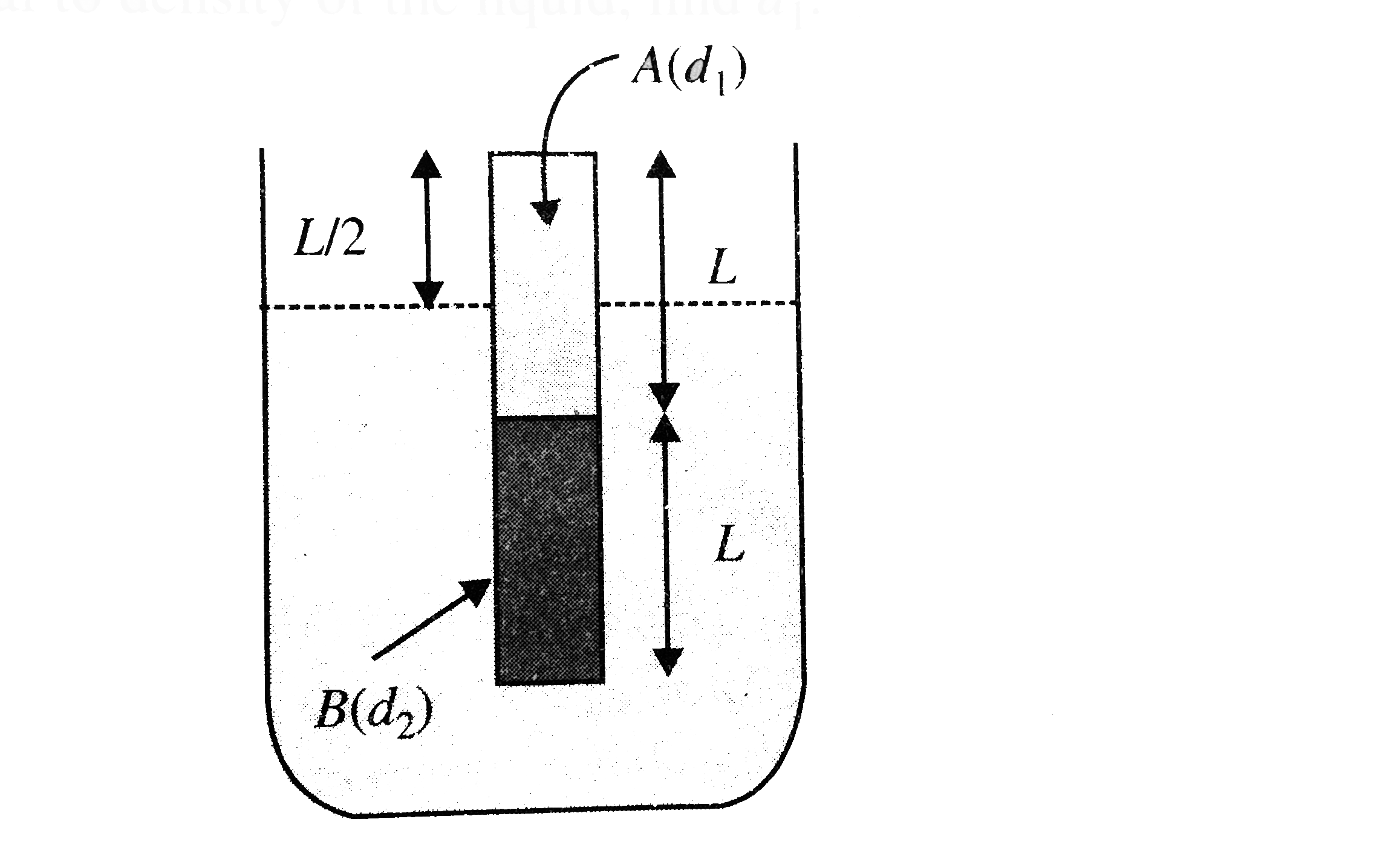
View Solution
