A solid cylinder of denisty ρ0, cross-section area A and length l floats in a liquid ρ(>ρ0 with its axis vertical, . If it is slightly displaced downward and released, the time period will be :
2π√lg
2π√ρ0lρg
2π√ρlρ0g
2π√l2g
The correct Answer is:B
To solve the problem of finding the time period of a solid cylinder floating in a liquid, we can follow these steps:
1. Identify the Given Parameters:
- Density of the cylinder: ρ0
- Density of the liquid: ρ (where ρ>ρ0)
- Cross-sectional area of the cylinder: A
- Length of the cylinder: l
2. Establish Equilibrium Condition:
- When the cylinder is floating in equilibrium, the weight of the cylinder is equal to the buoyant force acting on it.
- Weight of the cylinder:
W=ρ0⋅g⋅V=ρ0⋅g⋅(A⋅l)
- Buoyant force:
Fb=ρ⋅g⋅Vdisplaced=ρ⋅g⋅(A⋅h)
- Setting these equal gives:
ρ0⋅g⋅(A⋅l)=ρ⋅g⋅(A⋅h)
- Canceling g and A from both sides:
ρ0⋅l=ρ⋅h
- Rearranging gives:
h=ρ0ρ⋅l
3. Displace the Cylinder:
- Let the cylinder be displaced downward by a small distance y. The new submerged depth becomes h+y.
4. Calculate the Restoring Force:
- The new buoyant force when displaced:
F′b=ρ⋅g⋅(A⋅(h+y))=ρ⋅g⋅(A⋅h+A⋅y)
- The change in buoyant force (restoring force) when displaced downward:
Frestoring=F′b−W=ρ⋅g⋅(A⋅(h+y))−ρ0⋅g⋅(A⋅l)
- Substituting h from the equilibrium condition:
Frestoring=ρ⋅g⋅(A⋅(ρ0ρ⋅l+y))−ρ0⋅g⋅(A⋅l)
- Simplifying gives:
Frestoring=ρ⋅g⋅A⋅y
5. Use Newton's Second Law:
- According to Newton's second law:
Frestoring=m⋅a
- The mass m of the cylinder is ρ0⋅A⋅l:
ρ⋅g⋅A⋅y=ρ0⋅A⋅l⋅a
- The acceleration a can be expressed as d2ydt2:
ρ⋅g⋅y=ρ0⋅l⋅d2ydt2
6. Formulate the Differential Equation:
- Rearranging gives:
d2ydt2+ρgρ0ly=0
- This is a simple harmonic motion equation with angular frequency ω2=ρgρ0l.
7. Find the Time Period:
- The time period T is given by:
T=2π√mk=2π√ρ0lρg
Final Answer:
The time period T of the oscillating cylinder is:
T=2π√ρ0lρg
- Density of the cylinder: ρ0
- Density of the liquid: ρ (where ρ>ρ0)
- Cross-sectional area of the cylinder: A
- Length of the cylinder: l
- When the cylinder is floating in equilibrium, the weight of the cylinder is equal to the buoyant force acting on it.
- Weight of the cylinder:
W=ρ0⋅g⋅V=ρ0⋅g⋅(A⋅l)
- Buoyant force:
Fb=ρ⋅g⋅Vdisplaced=ρ⋅g⋅(A⋅h)
- Setting these equal gives:
ρ0⋅g⋅(A⋅l)=ρ⋅g⋅(A⋅h)
- Canceling g and A from both sides:
ρ0⋅l=ρ⋅h
- Rearranging gives:
h=ρ0ρ⋅l
- Let the cylinder be displaced downward by a small distance y. The new submerged depth becomes h+y.
- The new buoyant force when displaced:
F′b=ρ⋅g⋅(A⋅(h+y))=ρ⋅g⋅(A⋅h+A⋅y)
- The change in buoyant force (restoring force) when displaced downward:
Frestoring=F′b−W=ρ⋅g⋅(A⋅(h+y))−ρ0⋅g⋅(A⋅l)
- Substituting h from the equilibrium condition:
Frestoring=ρ⋅g⋅(A⋅(ρ0ρ⋅l+y))−ρ0⋅g⋅(A⋅l)
- Simplifying gives:
Frestoring=ρ⋅g⋅A⋅y
- According to Newton's second law:
Frestoring=m⋅a
- The mass m of the cylinder is ρ0⋅A⋅l:
ρ⋅g⋅A⋅y=ρ0⋅A⋅l⋅a
- The acceleration a can be expressed as d2ydt2:
ρ⋅g⋅y=ρ0⋅l⋅d2ydt2
- Rearranging gives:
d2ydt2+ρgρ0ly=0
- This is a simple harmonic motion equation with angular frequency ω2=ρgρ0l.
- The time period T is given by:
T=2π√mk=2π√ρ0lρg
The time period T of the oscillating cylinder is:
T=2π√ρ0lρg
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)
30 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
43 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercise
18 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
Consider a solid cylinder of the density ρs cross section area A and h ploating in a liquid of density ρl as shown in figure (ρl>ρs) . It is depressed sligtly and allowed to oscillation.

View SolutionA cylindrical object of outer diameter 20 cm and mass 2 kg floats in water with its axis vertical. If it is slightly depressed and then released, find the time period of the resulting simple harmonic motion of the object.
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
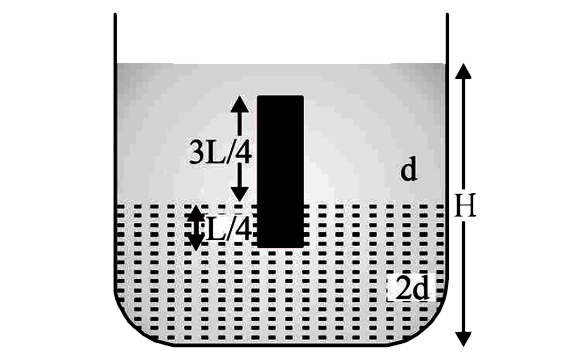
View SolutionA cylindrical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When pressed a little and the released the block starts oscillating. The period oscillations is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,
The density D of the material of the floating cylinder is
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H2), cross-sectional area A/5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L/4 denser liquid. Determine
(a) density D of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure =P0).
 .
.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial value of x is
View Solution
