A: If a spring block system, oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain same.
R: The time period of spring block system does not depend on g.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2)
If Assertion is true statement but Reason is false then mark (3)
If both Assertion and Reason are false statements, then mark (4)
The correct Answer is:B
To solve the question, we need to analyze the assertion (A) and the reason (R) provided:
Assertion (A): If a spring block system oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain the same.
Reason (R): The time period of a spring block system does not depend on g (acceleration due to gravity).
1. Understanding the Time Period of a Spring Block System:
The time period T of a spring block system is given by the formula:
T=2π√mk
where m is the mass of the block and k is the spring constant.
2. Analyzing the Effect of Gravity:
The formula for the time period of a simple pendulum is:
T=2π√lg
Here, l is the length of the pendulum and g is the acceleration due to gravity. Notice that this formula is dependent on g.
3. Comparing Oscillation in Vertical and Horizontal Planes:
When the spring block system is oscillating in a vertical plane, the effective force acting on the mass due to gravity affects the equilibrium position of the spring. However, the time period of oscillation is determined by the mass and spring constant, not by gravity.
4. Equilibrium Position:
When the spring block system is moved to oscillate on a horizontal surface, the effect of gravity is not directly influencing the oscillation in terms of time period. The equilibrium position changes, but the ratio lg remains constant because as g changes, the equilibrium position l also adjusts accordingly.
5. Conclusion:
Since the time period of the spring block system does not depend on g, we conclude that:
- The assertion (A) is true.
- The reason (R) is also true and correctly explains the assertion.
Thus, the final answer is that both the assertion and reason are correct, and the reason is a correct explanation of the assertion.
Final Answer:
Both assertion and reason are correct, and the reason is a correct explanation of the assertion.
---
The time period T of a spring block system is given by the formula:
T=2π√mk
where m is the mass of the block and k is the spring constant.
The formula for the time period of a simple pendulum is:
T=2π√lg
Here, l is the length of the pendulum and g is the acceleration due to gravity. Notice that this formula is dependent on g.
When the spring block system is oscillating in a vertical plane, the effective force acting on the mass due to gravity affects the equilibrium position of the spring. However, the time period of oscillation is determined by the mass and spring constant, not by gravity.
When the spring block system is moved to oscillate on a horizontal surface, the effect of gravity is not directly influencing the oscillation in terms of time period. The equilibrium position changes, but the ratio lg remains constant because as g changes, the equilibrium position l also adjusts accordingly.
Since the time period of the spring block system does not depend on g, we conclude that:
- The assertion (A) is true.
- The reason (R) is also true and correctly explains the assertion.
Both assertion and reason are correct, and the reason is a correct explanation of the assertion.
Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH INSTITUTE ENGLISHChapter:OSCILLATIONSExercise:Assignment (Section C) (PREVIOUS YEARS QUESTIONS)
Explore 43 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- PHYSICAL WORLDBook:AAKASH INSTITUTE ENGLISHChapter:PHYSICAL WORLDExercise:ASSIGNMENT (Section-B)
Explore 4 Videos
Similar Questions
Time period of a given spring-mass system is

View SolutionIn a spring-block system, match the following:
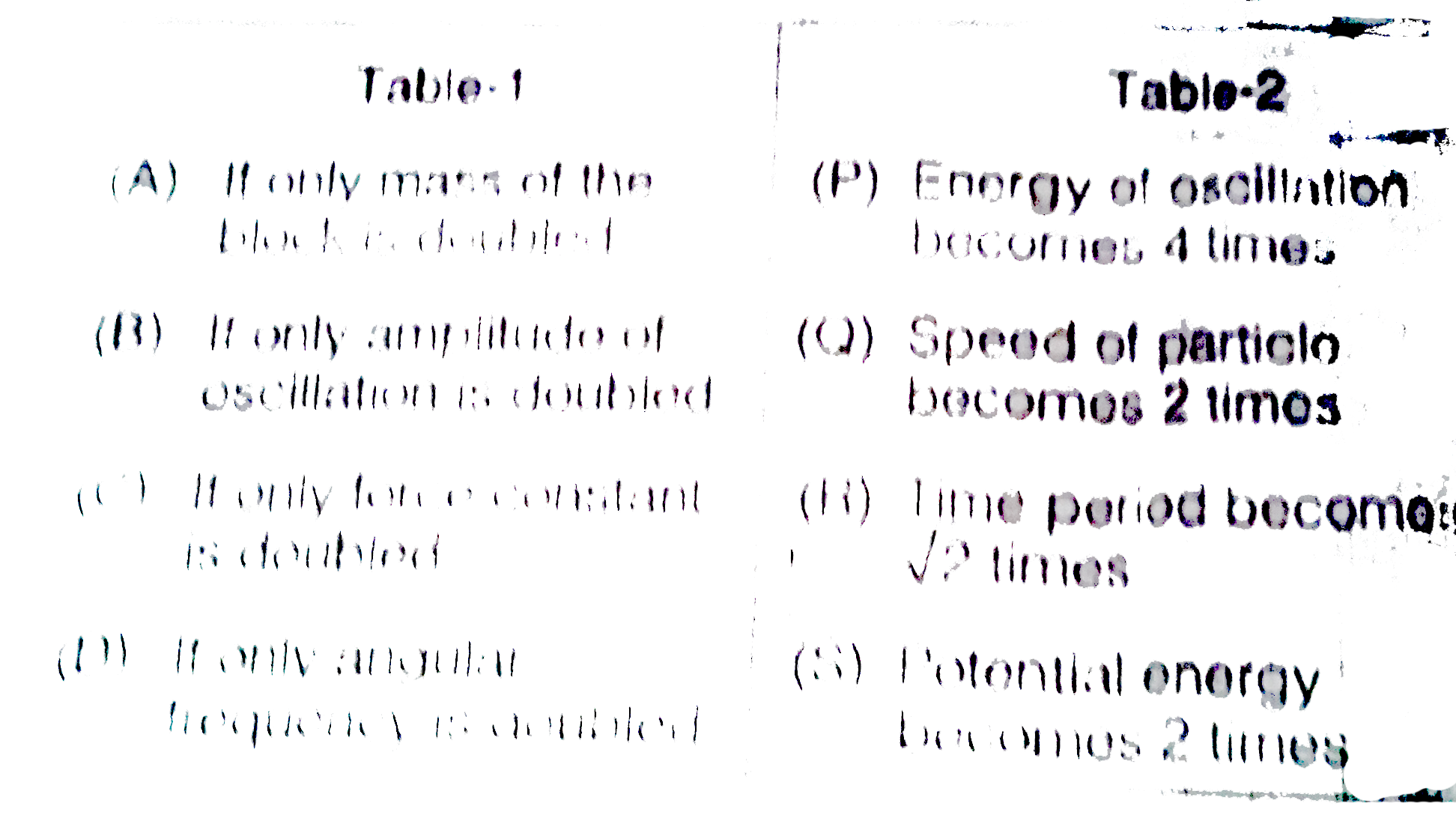
View SolutionA loaded spring is made to oscillate on the Earth surface and then in moon. Will there be any change in the time period ?
View SolutionIn spring-block system match the following

View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
View SolutionFind the period of a vertical spring - block system by both methods.
View SolutionA spring is made to oscillate horizontally and vertically. Will there be any change in the period ?
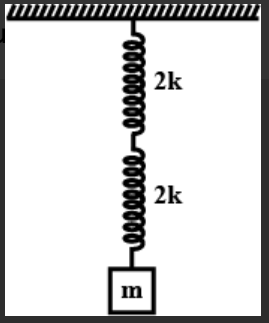
View SolutionThe time period of oscillation of the block as shown in figure is
View SolutionComparing the L-C oscillations with the oscillations of a spring-block system
View SolutionA spring-block system undergoes vertical oscillations above a large horizontal metal sheet with uniform positive charge. The time period of the oscillations is T. If the block is given a charge Q, its time period of oscillation will be
View Solution
