Statement - 1 : If a concentric spheerical Gaussian surface is drawn inside thin spheical shell charge, electric field (E) at each point of surface must be zero.
Statement - 2 : In accordance with Gauss's law
ϕE=∮→E.d→A=Qnet enclosedε0
Qnet enclosed=0 implies ϕE=0
To solve the problem, we need to analyze both statements provided in the question and determine their validity based on the principles of electrostatics and Gauss's law.
1. Understanding Statement 1:
- The first statement claims that if a concentric spherical Gaussian surface is drawn inside a thin spherical shell (which is uniformly charged), the electric field (E) at each point of the surface must be zero.
- According to electrostatics, a charged spherical shell produces an electric field only outside the shell. Inside the shell, the electric field is indeed zero due to the symmetry of the charge distribution. Therefore, this statement is true.
2. Understanding Statement 2:
- The second statement refers to Gauss's law, which states that the electric flux (Φ_E) through a closed surface is equal to the net charge (Q_net enclosed) within that surface divided by the permittivity of free space (ε₀).
- For a Gaussian surface drawn inside a thin spherical shell, the net charge enclosed (Q_net) is zero because there is no charge inside the shell. According to Gauss's law, this implies that the electric flux Φ_E is also zero.
- Since Φ_E = ∮ E · dA = 0, this means that the electric field (E) at every point on the Gaussian surface must also be zero. Therefore, this statement is also true.
3. Conclusion:
- Statement 1 is true because the electric field inside a charged spherical shell is zero.
- Statement 2 is true because the electric flux through the Gaussian surface is zero due to the absence of enclosed charge.
- Therefore, both statements are true, but Statement 1 is not correctly interpreted in the context of the question.
Final Answer:
- Statement 1 is true and Statement 2 is true. The correct interpretation is that the electric field inside the shell is zero.
- The first statement claims that if a concentric spherical Gaussian surface is drawn inside a thin spherical shell (which is uniformly charged), the electric field (E) at each point of the surface must be zero.
- According to electrostatics, a charged spherical shell produces an electric field only outside the shell. Inside the shell, the electric field is indeed zero due to the symmetry of the charge distribution. Therefore, this statement is true.
- The second statement refers to Gauss's law, which states that the electric flux (Φ_E) through a closed surface is equal to the net charge (Q_net enclosed) within that surface divided by the permittivity of free space (ε₀).
- For a Gaussian surface drawn inside a thin spherical shell, the net charge enclosed (Q_net) is zero because there is no charge inside the shell. According to Gauss's law, this implies that the electric flux Φ_E is also zero.
- Since Φ_E = ∮ E · dA = 0, this means that the electric field (E) at every point on the Gaussian surface must also be zero. Therefore, this statement is also true.
- Statement 1 is true because the electric field inside a charged spherical shell is zero.
- Statement 2 is true because the electric flux through the Gaussian surface is zero due to the absence of enclosed charge.
- Therefore, both statements are true, but Statement 1 is not correctly interpreted in the context of the question.
- Statement 1 is true and Statement 2 is true. The correct interpretation is that the electric field inside the shell is zero.
Similar Questions
In Gauss's law ε0∮→E.¯¯¯¯ds=Qenclosed, is →E only due to charges enclosed ?
View SolutionA : We may have a Gaussian surface in which less number of field lines enter and more field lines come out.
R : The electric field E in the Gauss's law is only due to the enclosed charges.View SolutionIf charge q1 and q2 lies inside and outside respectively of a closed surface S. Let E be the electric field at any point on S and ϕ be the electric flux over S. Select the incorrect option.
View Solutionfive charge q1,q2,q3,q4and q5 are fixed at their positions as shown in figure .s is Gaussian surface .The Gauss's law is given by ∮→E.→ds=qε0
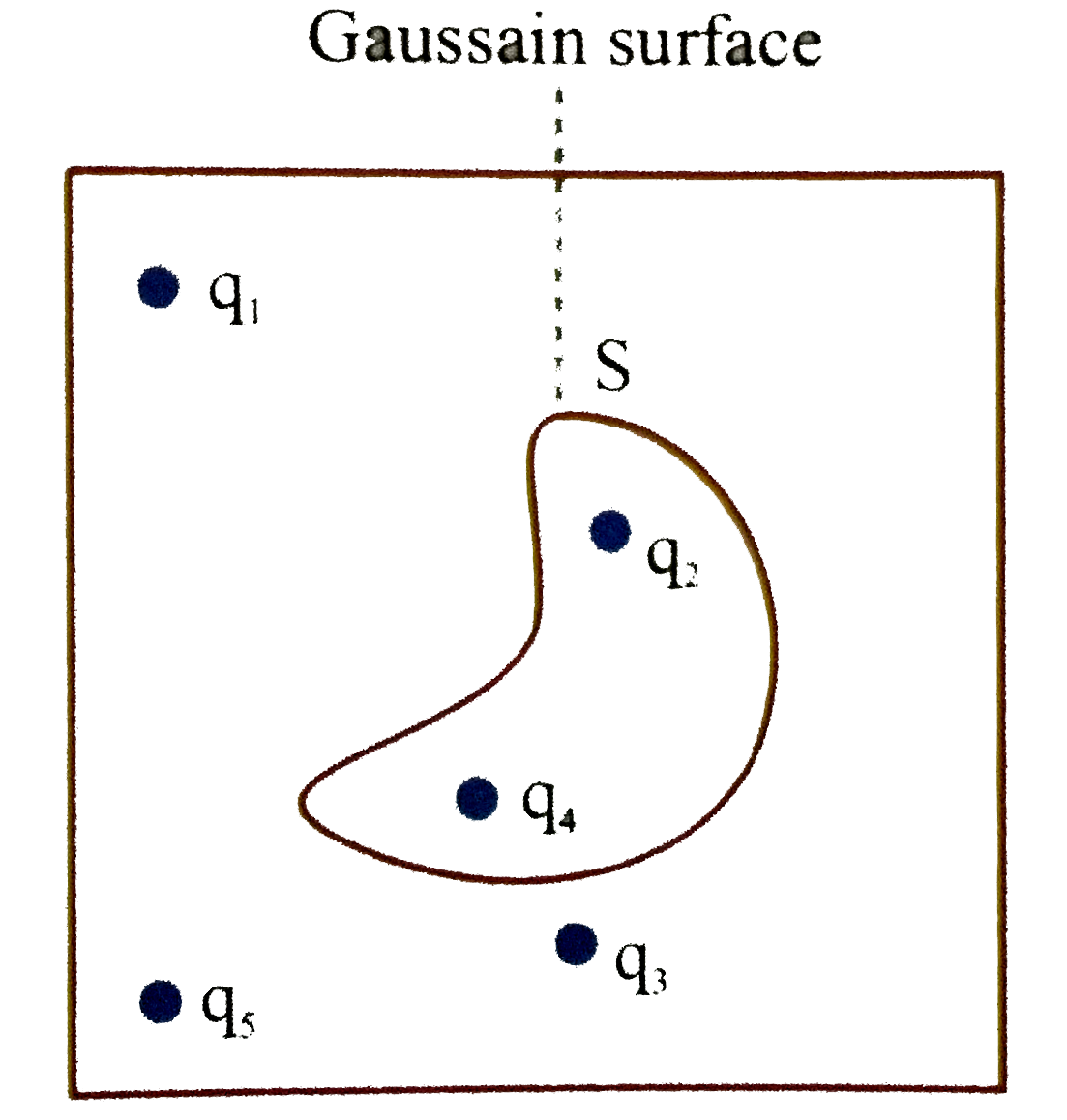
Which of the following statement is correct?View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.View SolutionStatement 1: Electric field produced by changing magnetic field is nonconservative.
Statement 2: For the electric field →E induced by a changing magnetic field which has closed lines of force, ∮→E.→dl=0View SolutionConsider the situation shown in figure. We find electric field E at point P using Gauss's law and it comes out to be E=σ/ε0. This electric field is due to
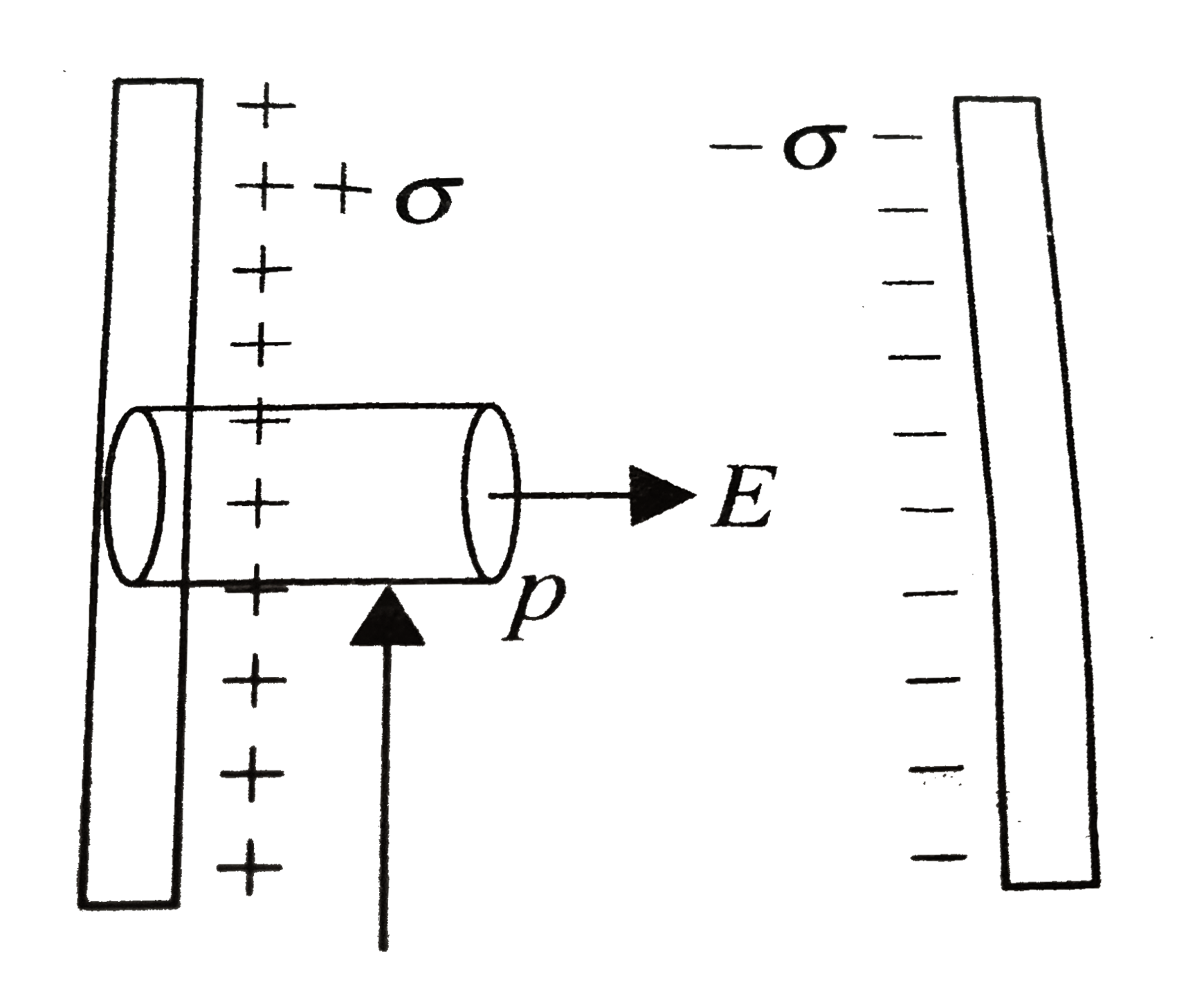 View Solution
View SolutionUsing Gauss. theorem, obtain an expression for intensity of electric field .E. at a point which is at a distance r (r>R) from the centre Cof a thin spherical shell (of radius R) carrying charge.Q.
View SolutionIf electric field around a surface is given by ∣∣→E∣∣=Q∈ε0|A| where 'A' is the normal area of surface and Q∈ is the charge enclosed by the surface. This relation of gauss's law is valid when
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
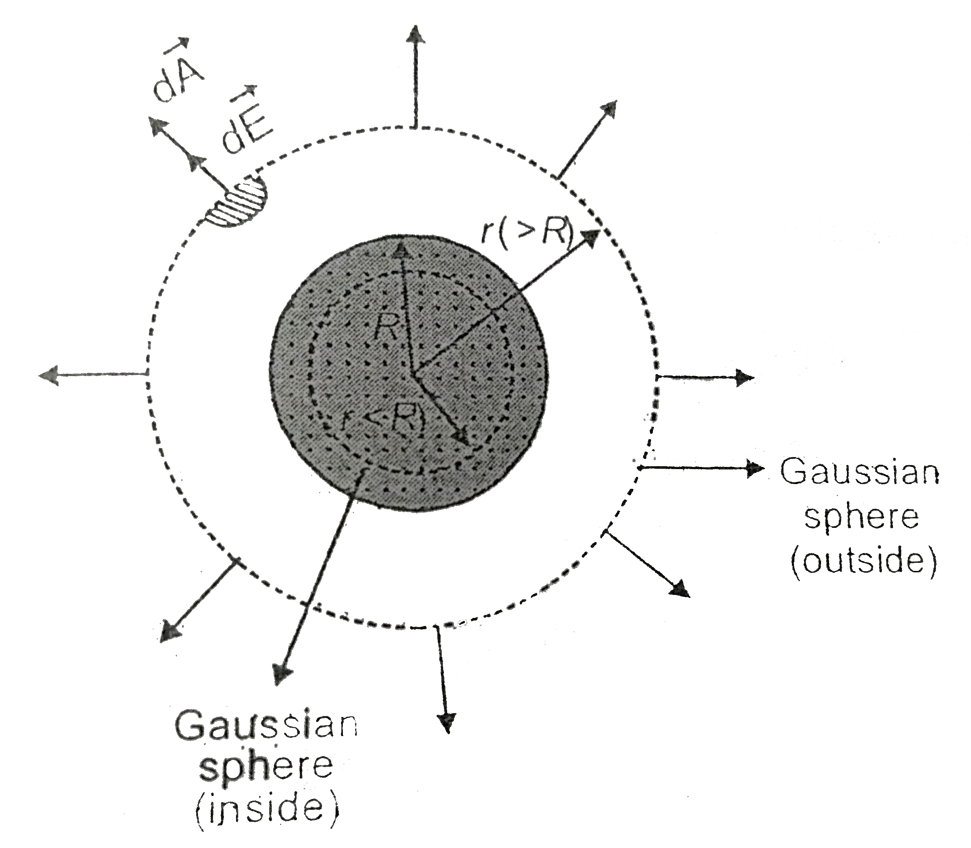
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]
 View Solution
View Solution
