five charge q1,q2,q3,q4and q5 are fixed at their positions as shown in figure .s is Gaussian surface .The Gauss's law is given by ∮→E.→ds=qε0
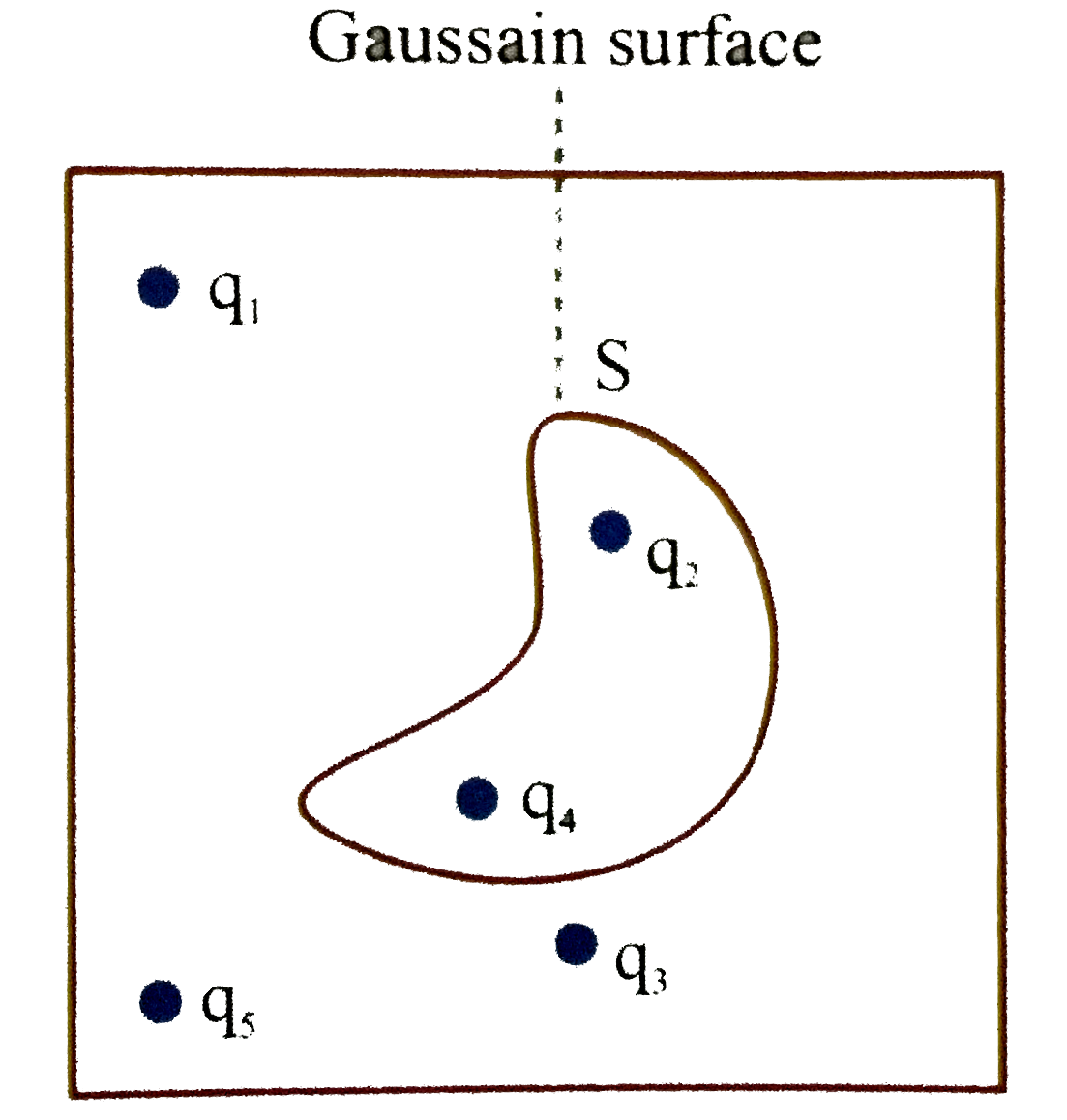
Which of the following statement is correct?
E on the LHS of the above equation will have a contribution from q1,q5andq3 while q on the RHS will have a contribution from q2andq4 only.
E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2andq4 only.
E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1,q3andq5 only
Both E on the LHS and q on the RHS will have contributions from q2andq4 only.
The correct Answer is:B
According to Gauss' law, the term q on the right side of the equation ∫S.E.dS=qε0 includes the sum of all charges enclosed by the surface.
The charges may be located anywhere inside the surface, if the surface is so chosen that there are some charges inside and some outside, the electric field on the left side of equaiton is due to all the charges, both inside and outside S.
So, E on LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2andq4 only.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - MCQ s (More than One Options)
6 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Very short Type Question
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - LONG ANSWER TYPE QUESTION
5 Videos
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Long
11 Videos
Similar Questions
Five charges q1,q2,q3,q4andq5 are fixed at their positions as shown in figure. S is Gaussian surface. The Gauss's law is given by ∮→ES⋅→ds=qε0. Which of the following statements is correct?
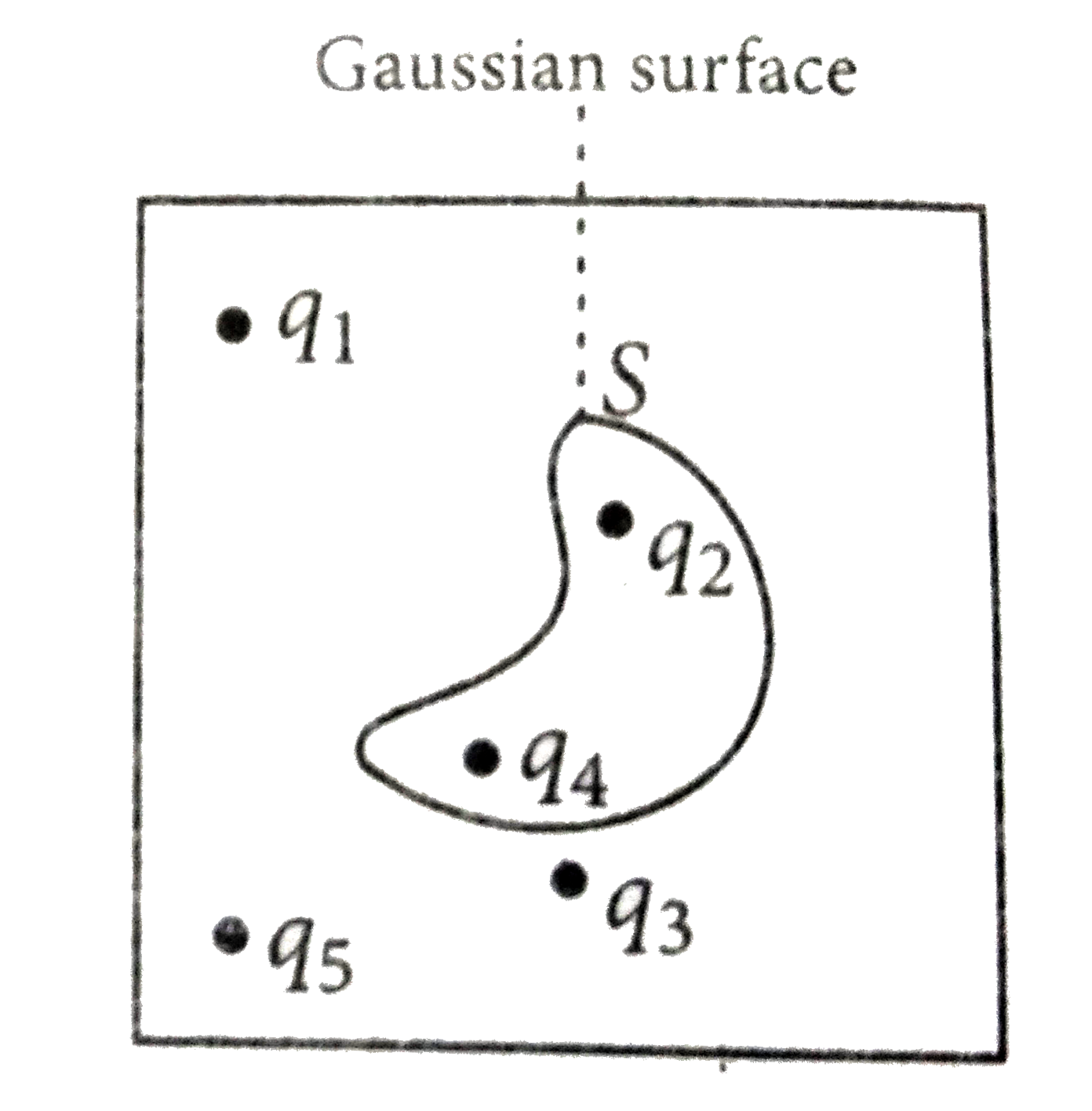
View Solutionq1,q2,q3 and q4 are point charges located at point as shown in the figure and s is a spherical Gaussian surface of radius R. Which of the following is true according to the Gauss's law

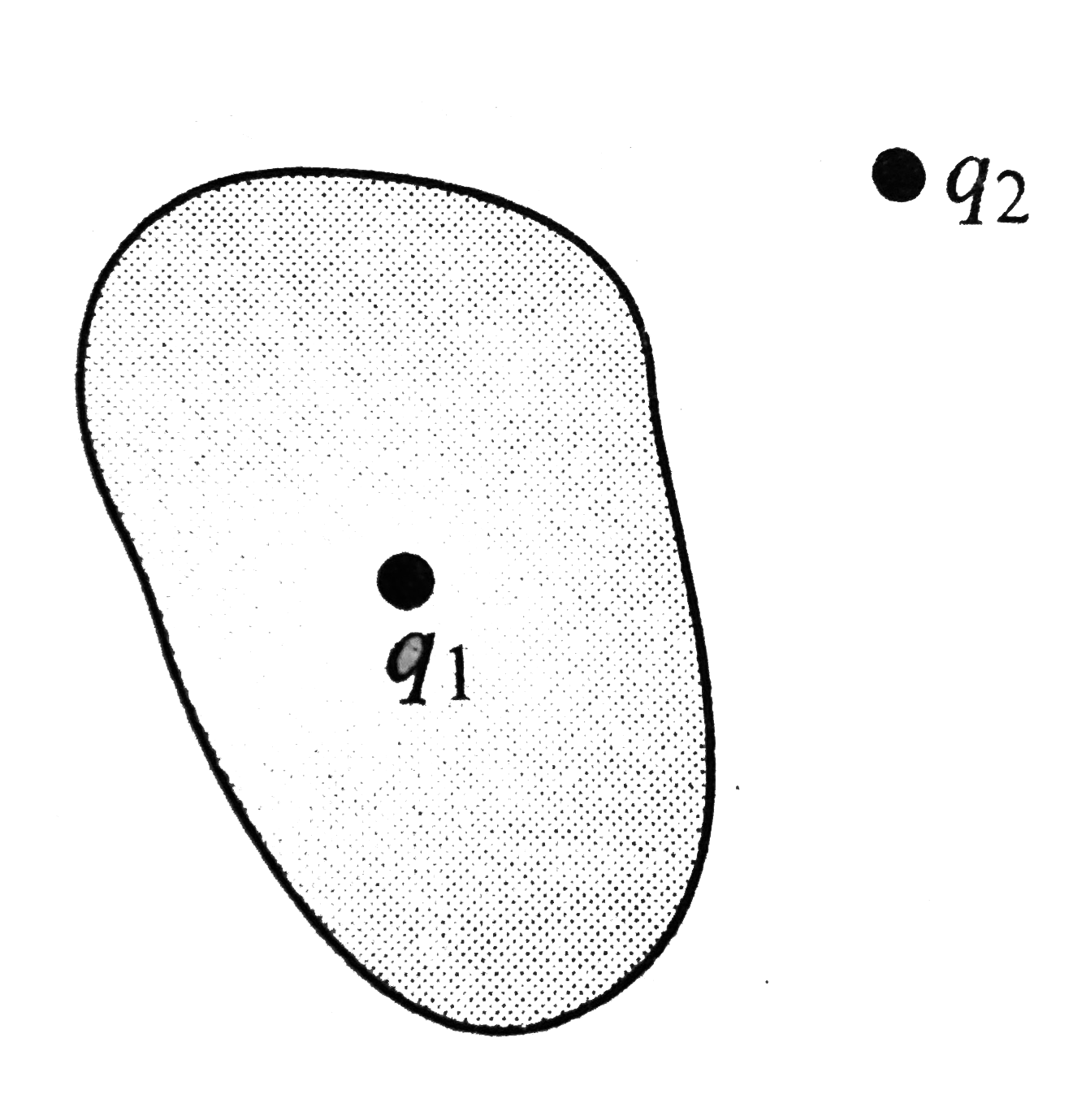
View SolutionConsider Gauss's law
∮→E⋅→ds=qε0
Then, for the situation shown in figure at the Gaussian surface
View SolutionTwo fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
View SolutionIn Gauss's law ε0∮→E.¯¯¯¯ds=Qenclosed, is →E only due to charges enclosed ?
View SolutionAssertion:- In a given situation of arrangement of charges, an extra charge is placed outside the Gaussion surface. In the Gauss Theroem
∮→Ed→s=Q∈ε0Q∈ remains unchanged whereas electric field →E at the site of the element is changed.
Reason:- Electric field →E at any point on the Gaussian surface is due to inside charge only.
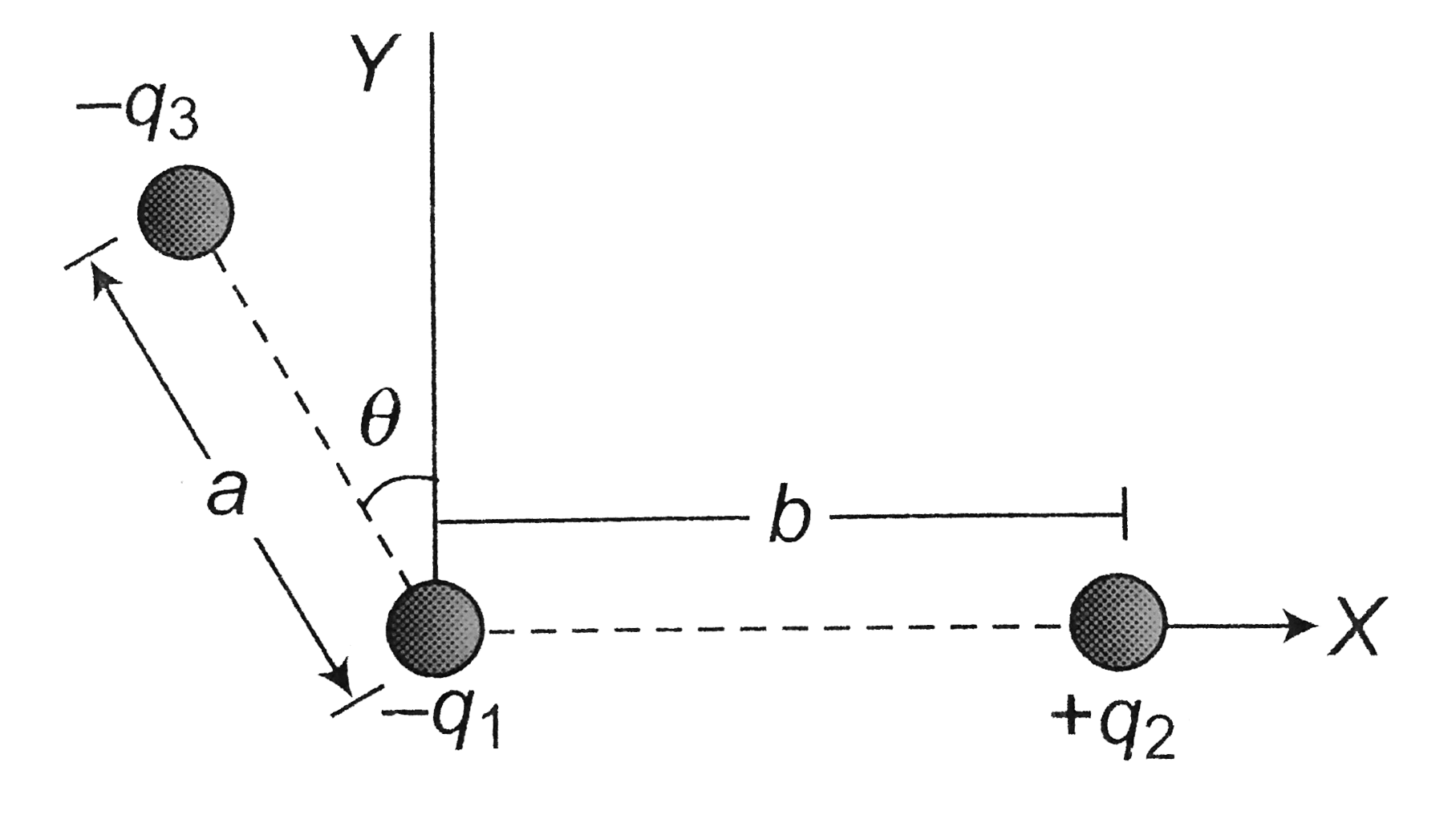
View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
View SolutionFigure shows four charges q1,q2,q3,andq4 fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is

View SolutionA few electric field lines for a system of two charges Q1 and Q2 fixed at two different points on the x-axis are shown in the figure. These lines suggest that
(i) |Q1|>|Q2|
(ii) |Q1|<|Q2|
(iii) At a finite distance to the left of Q1 the electric field is zero
(iv) At a finite distance to the right of Q2 the electric field is zero

View Solution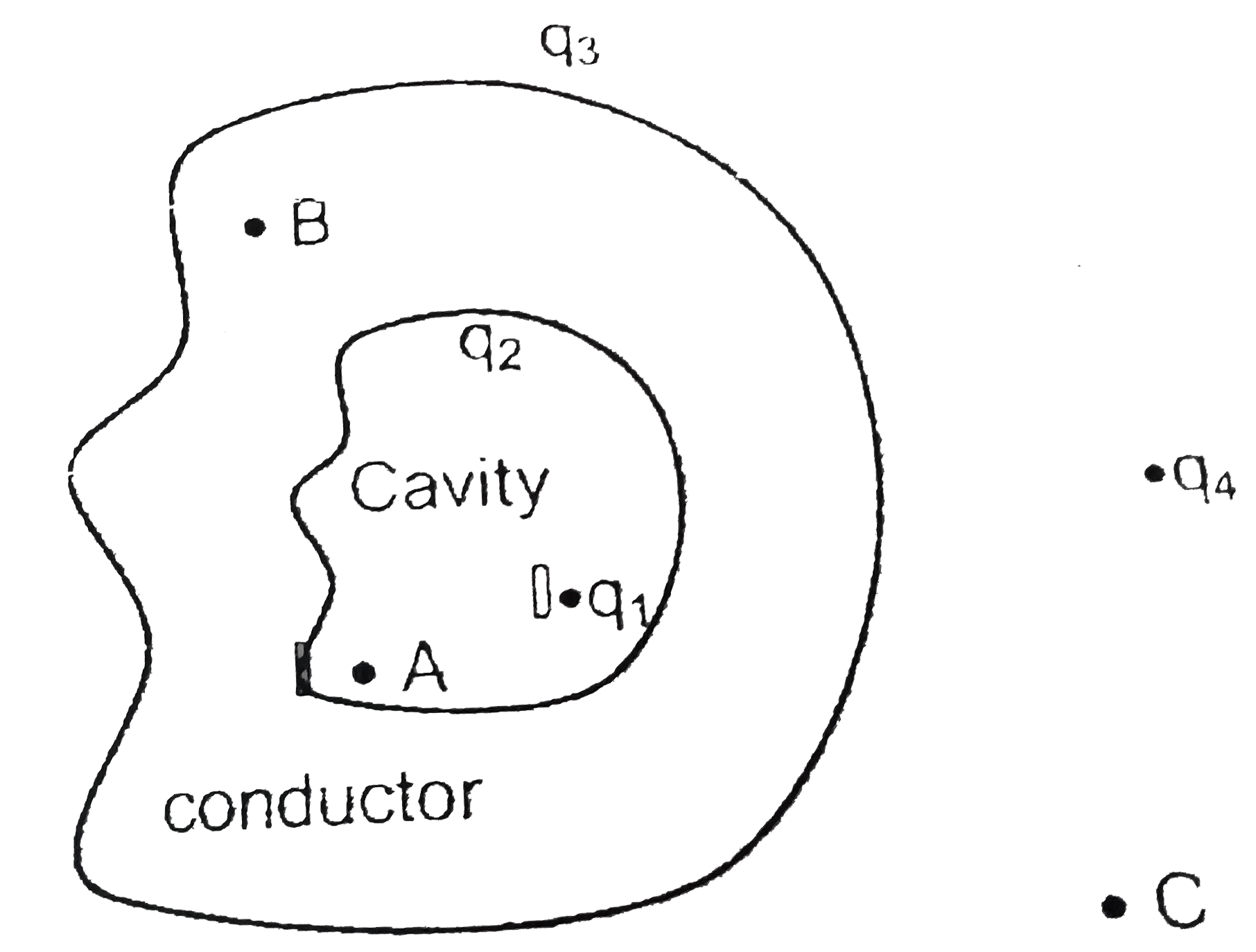
We have a fixed conductor having a cavity inside. There is a point charge q1 kept inside the cavity charge appearing at the inner surface of the cavity is q2. Charge appearing at outer surface of conductor is q3 and there lies another point charge q4 out side the conductor. Whole situation is shown in figure. q4. is held stationary by applying an external force →F0 on it. Three points A, B and C are shown. Answer the following two questions.
Q. If keeping the magnitude and nature of q1 fixed position of q1 is changed inside the cavity. Then choose the correct option(s)
View Solution
