If electric field around a surface is given by ∣∣→E∣∣=Q∈ε0|A| where 'A' is the normal area of surface and Q∈ is the charge enclosed by the surface. This relation of gauss's law is valid when
Surface is equipotential
Magnitude of electric field is constant
Magnitude of electric field is constant & the surface is equipotential
For all Gaussian surfaces.
The correct Answer is:C
To solve the question regarding the validity of Gauss's law expressed as |→E|=Qinϵ0|A|, we need to analyze the conditions under which this relationship holds true.
1. Understanding Gauss's Law: Gauss's law states that the electric flux ΦE through a closed surface is proportional to the charge Qin enclosed by that surface. Mathematically, it is expressed as:
ΦE=∮→E⋅d→A=Qinϵ0
where →E is the electric field and d→A is the differential area vector on the surface.
2. Electric Flux Calculation: The electric flux through a surface can be calculated as:
ΦE=∫→E⋅d→A
If the electric field is uniform and constant over the surface, we can simplify this to:
ΦE=→E⋅→A=E|A|cosθ
where θ is the angle between the electric field vector and the area vector.
3. Conditions for the Formula: For the relation |→E|=Qinϵ0|A| to hold, we need:
- The electric field →E must be uniform across the surface.
- The angle θ between →E and the area vector →A must be zero (i.e., cosθ=1), which implies that the electric field is perpendicular to the surface.
4. Conclusion: Therefore, the relation is valid under the following conditions:
- The electric field is constant in magnitude and direction across the surface.
- The surface is an equipotential surface, meaning that the electric field lines are perpendicular to the surface.
Final Answer:
The relation of Gauss's law |→E|=Qinϵ0|A| is valid when:
- The electric field is uniform (constant in magnitude and direction).
- The surface is equipotential (electric field lines are perpendicular to the surface).
ΦE=∮→E⋅d→A=Qinϵ0
where →E is the electric field and d→A is the differential area vector on the surface.
ΦE=∫→E⋅d→A
If the electric field is uniform and constant over the surface, we can simplify this to:
ΦE=→E⋅→A=E|A|cosθ
where θ is the angle between the electric field vector and the area vector.
- The electric field →E must be uniform across the surface.
- The angle θ between →E and the area vector →A must be zero (i.e., cosθ=1), which implies that the electric field is perpendicular to the surface.
- The electric field is constant in magnitude and direction across the surface.
- The surface is an equipotential surface, meaning that the electric field lines are perpendicular to the surface.
The relation of Gauss's law |→E|=Qinϵ0|A| is valid when:
- The electric field is uniform (constant in magnitude and direction).
- The surface is equipotential (electric field lines are perpendicular to the surface).
Topper's Solved these Questions
Similar Questions
Show that the electric field at the surface of a charged conductor is given by →E=σε0ˆn , where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction .
View SolutionIn fiinding the electric field using Gauses law the formula ∣∣→E∣∣=qenc∈0|A| is applicable. In the Formula. ∈0 is permittivity of free space, A is the area of Gaussian surface and qenc is charge enclosed by the Gaussion surface. This equation can be used in which of the following situation?
View SolutionWhy the electric field at the outer surface of a hollow charged conductor is normal to the surface?
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
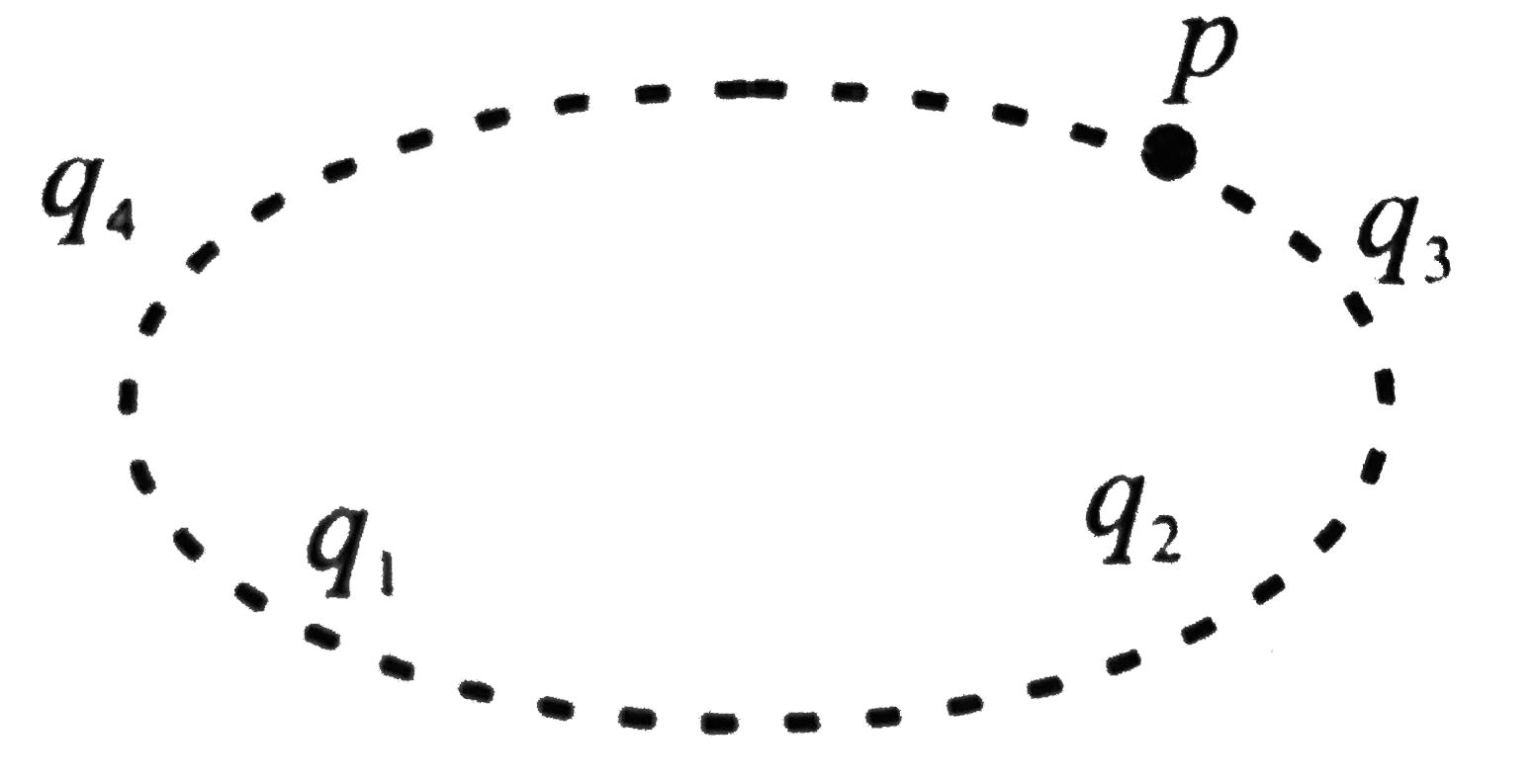
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface due to q3 and q4 is
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when qencl is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
The net flux of the electric field through the surface is
View SolutionA charge Q is enclosed by a Gaussian surface. If surface area is doubled and charge Q is tripled then the outward electric flux will
View SolutionFigure shows a conducting sphere with a cavity. A point charge q1 is placed inside cavity, and q2 is placed out side the sphere →Ein is electric field due to charge induced on surface of cavity. →Eout is electric field due to charge induced on outer surface of sphere and →Enet is net field at any point. Two closed gaussian surface S1 & S2 are also drawn in the figure.

View SolutionA solid insulating sphere of radius a carries a net positive charge 3Q, uniformly distributed throughout its volume. Concentric with this sphere is a conducting spherical shell with inner radius b and outer radius c and having a net charge -Q, as shown in figure

a. Consider a spherical Gaussian surface of radius rgtc, the net charge enclosed by this surface is .............
b. The direction of the electric field rgtc is .............
c. The electric field at rgtc is ............... .
d. The electric field in the region with radius r, which cgtrgtb, is ...............
e. Consider a spherical Gaussian surface of radius r, where c>r>b, the net charge enclosed by this surface is ................ .
f. Consider a spherical Gaussian surface of radius r, whereb>r>a, the net charge enclosed by this surface is ................. .
g. The electric field in the region b>r>a is ................ .
h. Consider a spherical Gaussian surface of radius r<a. Find an expression for the net charge Q(r) enclosed by this surface as a function of r. Note that the charge inside the surface is less than 3Q.
i. The electric field in the region r<a is ................. .
j. The charge on the inner surface of the conducting shell is .......... .
k. The charge on the outer surface of the conducting shell is .............. .
l. Make a plot of the magnitude of the electric field versus r.
View Solution
