Three charge q,Q and −4q are placed in a straight line , line of length Lat points distant 0,L/2 and L respectively from one end. In order to make the net force on q zero, the charge Q must be equal to
q
4q
−q2
−2q
The correct Answer is:A
To solve the problem, we need to find the value of charge Q such that the net force on charge q is zero. The charges are positioned as follows:
- Charge q is at position 0
- Charge Q is at position L2
- Charge −4q is at position L
1. Identify Forces Acting on Charge q:
- The force on charge q due to charge Q (at L2) is F2.
- The force on charge q due to charge −4q (at L) is F1.
2. Calculate the Force F1 due to Charge −4q:
- The distance between charge q and charge −4q is L.
- The force F1 is given by Coulomb's law:
F1=k|q⋅(−4q)|L2=k4q2L2
- Since −4q is negative, it attracts q towards it, so F1 acts to the right.
3. Calculate the Force F2 due to Charge Q:
- The distance between charge q and charge Q is L2.
- The force F2 is also given by Coulomb's law:
F2=k|q⋅Q|(L2)2=k4q|Q|L2
- The direction of F2 depends on the sign of Q. If Q is positive, F2 acts to the right (repulsive). If Q is negative, F2 acts to the left (attractive).
4. Set the Forces Equal for Equilibrium:
- For the net force on q to be zero, the magnitudes of the forces must be equal:
F1=F2
k4q2L2=k4q|Q|L2
5. Simplify the Equation:
- Cancel k and L2 from both sides:
4q2=4q|Q|
- Divide both sides by 4q (assuming q≠0):
q=|Q|
6. Determine the Value of Charge Q:
- Since Q can be positive or negative, we conclude:
Q=qorQ=−q
Conclusion:
To make the net force on charge q zero, the charge Q must be equal to q (since we are looking for the magnitude).
Final Answer:
Q=q
- Charge Q is at position L2
- Charge −4q is at position L
- The force on charge q due to charge Q (at L2) is F2.
- The force on charge q due to charge −4q (at L) is F1.
- The distance between charge q and charge −4q is L.
- The force F1 is given by Coulomb's law:
F1=k|q⋅(−4q)|L2=k4q2L2
- Since −4q is negative, it attracts q towards it, so F1 acts to the right.
- The distance between charge q and charge Q is L2.
- The force F2 is also given by Coulomb's law:
F2=k|q⋅Q|(L2)2=k4q|Q|L2
- The direction of F2 depends on the sign of Q. If Q is positive, F2 acts to the right (repulsive). If Q is negative, F2 acts to the left (attractive).
- For the net force on q to be zero, the magnitudes of the forces must be equal:
F1=F2
k4q2L2=k4q|Q|L2
- Cancel k and L2 from both sides:
4q2=4q|Q|
- Divide both sides by 4q (assuming q≠0):
q=|Q|
- Since Q can be positive or negative, we conclude:
Q=qorQ=−q
To make the net force on charge q zero, the charge Q must be equal to q (since we are looking for the magnitude).
Q=q
Similar Questions
Three charges −q,+Q and −q are placed in a straight line as shown

If the total potential energy of the system is zero, then the ratio qQ is
View SolutionThree charges -q,+2q, and -q are arranged on a line as shown in fig. Calculate the field at a distance r>>a on the line.
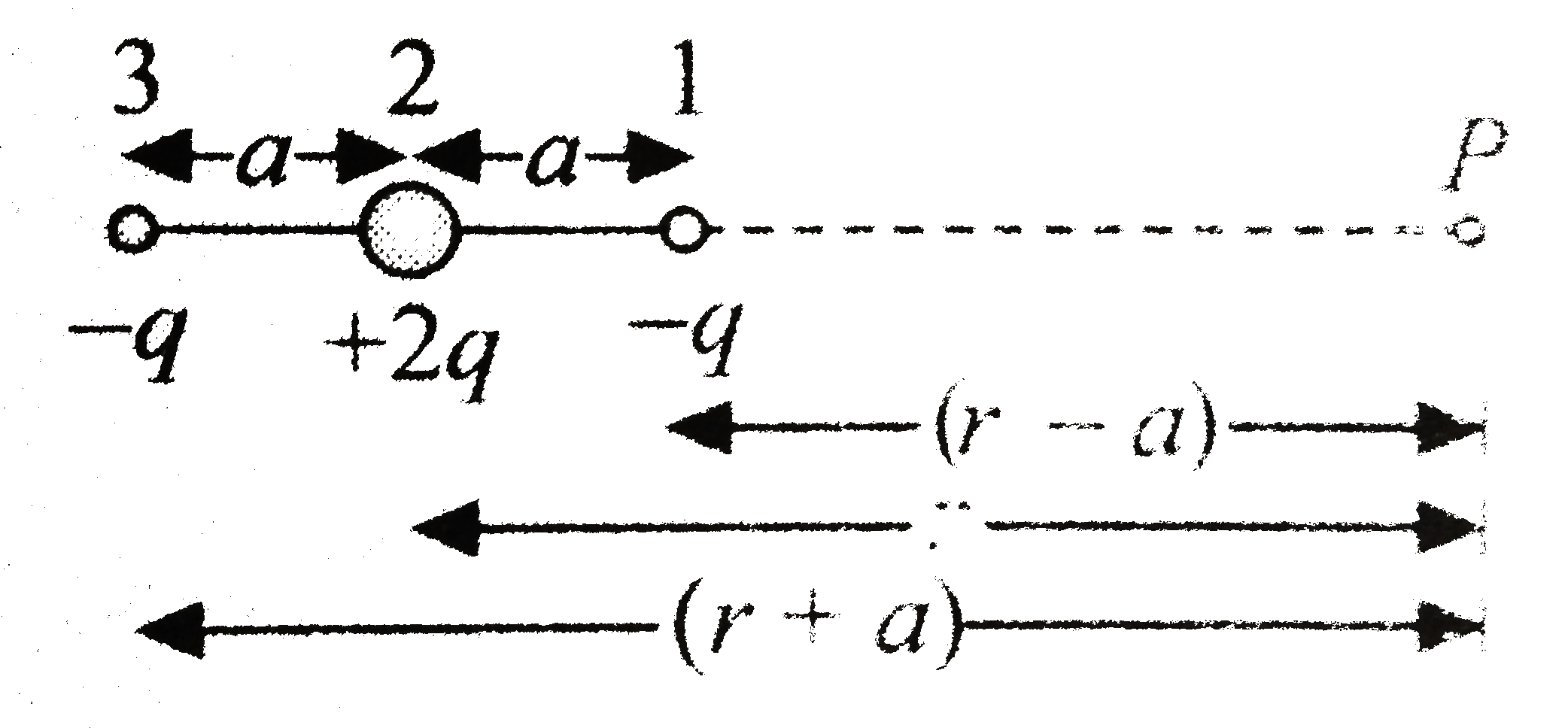
View SolutionThree point charge Q,4Q and 16Q are placed on a straight line 9cm long.Charges are placed in such a way that the system has minimum potential energy .Then
View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .
.
View SolutionThree point charges -Q, Q and Q are placed on a straight line with distance d between charges as shown. Find the magnitude of the electric field at the point P in the configuration shown which is at a distance a from middle charge Q in the system provided that a>>d. Take 2Qd=p.

View SolutionTwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
View SolutionCharges 4Q, q and Q and placed along x-axis at positions x=0,x=1/2 and x=1, respectively. Find the value of q so that force on charge Q is zero
View SolutionThree charges +q , +q, and Q are placed at the comers of a right angled isosceles triangle as shown in the figure. If the net potential energy of the system is zero then value of Q is
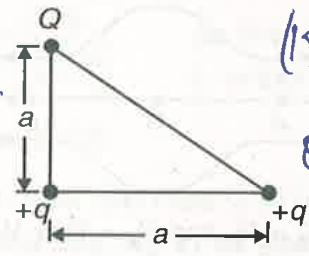
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View Solution