The force on a charge situated on the axis of a small dipole is F .If the charge is shifted to double the distance the force acting will be fx .What is x ?
4F
F2
F4
F8
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the force acting on a charge due to a dipole and the distance from the dipole. Here are the steps to arrive at the solution:
Step 1: Understand the Initial Setup
- We have a small electric dipole and a charge Q located at a distance R from the center of the dipole along its axial line.
- The force F acting on the charge Q due to the dipole can be expressed as:
F=Q⋅E
where E is the electric field due to the dipole at distance R.
Step 2: Electric Field of a Dipole
- The electric field E on the axial line of a dipole is given by:
E∝1R3
- Therefore, the force F can be expressed as:
F∝1R3
Step 3: Shift the Charge to Double the Distance
- Now, if the charge is moved to double the distance, the new distance R′ becomes:
R′=2R
Step 4: Calculate the New Force
- The new electric field E′ at distance R′ is:
E′∝1(2R)3=18R3
- Thus, the new force F′ acting on the charge Q at this new distance is:
F′∝1(2R)3=F8
Step 5: Relate the New Force to the Original Force
- From the relationship derived, we have:
F′=F8
- This indicates that the new force F′ is Fx where x=8.
Conclusion
- Therefore, the value of x is:
x=8
- We have a small electric dipole and a charge Q located at a distance R from the center of the dipole along its axial line.
- The force F acting on the charge Q due to the dipole can be expressed as:
F=Q⋅E
where E is the electric field due to the dipole at distance R.
- The electric field E on the axial line of a dipole is given by:
E∝1R3
- Therefore, the force F can be expressed as:
F∝1R3
- Now, if the charge is moved to double the distance, the new distance R′ becomes:
R′=2R
- The new electric field E′ at distance R′ is:
E′∝1(2R)3=18R3
- Thus, the new force F′ acting on the charge Q at this new distance is:
F′∝1(2R)3=F8
- From the relationship derived, we have:
F′=F8
- This indicates that the new force F′ is Fx where x=8.
- Therefore, the value of x is:
x=8
Similar Questions
An electric dipole is placed at a distance x from centre O on the axis of a charged ring of R and charge Q uniformly distributed over it.
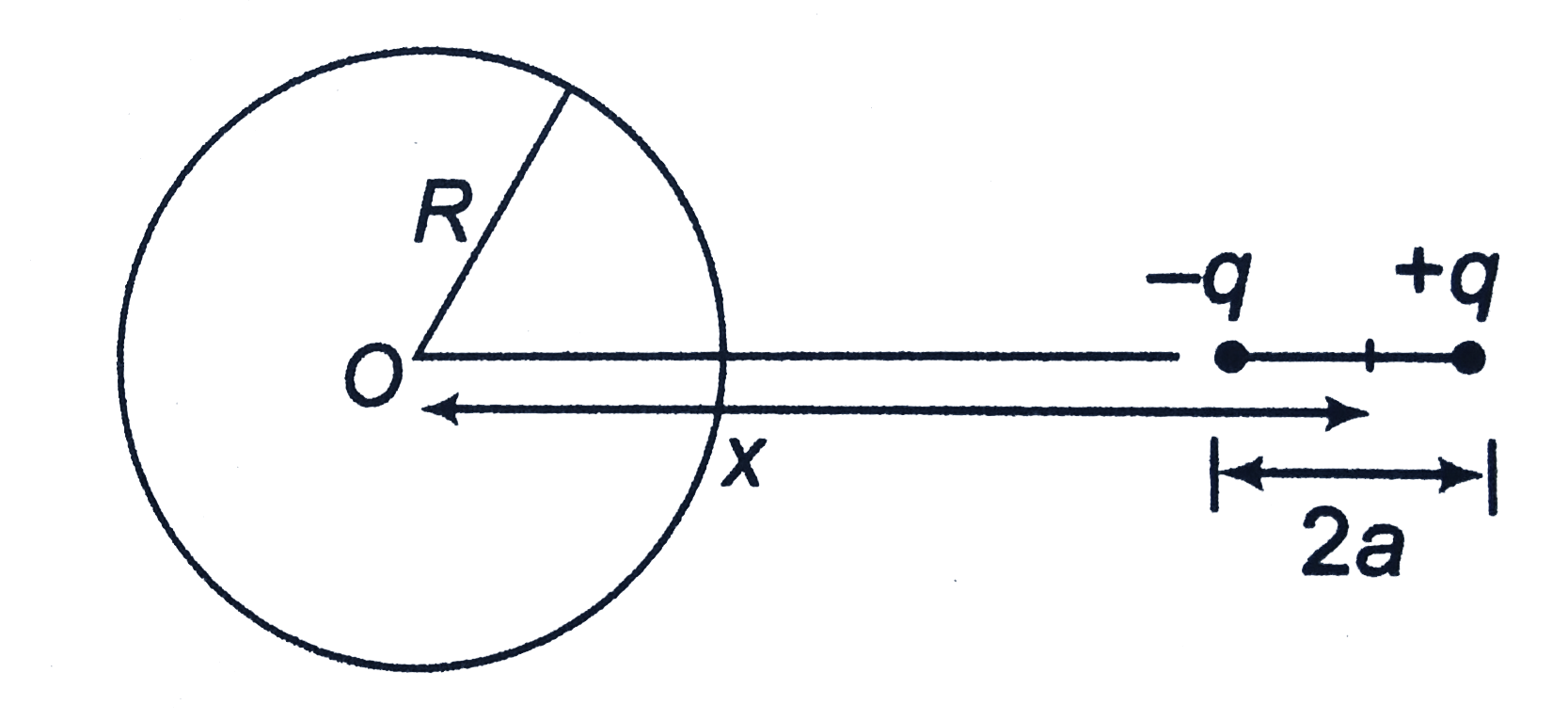
(a) Find the net force acting on the dipole.
(b) What is the work done in rotating the dipole through 180∘?
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View SolutionThe force between two point electric charges kept at a distance d apart in air is F. If these charges are kept at the sme distance in water, the force between the charges is F'. The ratio F'/F is equal to ……….. .
View SolutionForce acting upon charged particle kept between the plates of a charged condenser is F. If one of the plates of the condenser is removed, force acting on the same particle will become.
View SolutionTwo charges of equal magnitudes and at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionIf the force exerted by an electric dipole on a charge q at distance of 1 m is F, the force at a point 2 m away in the same direction will be
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

[(a) (find the net force acting on the dipole b) The work done external agent in rotating the dipole through 180∘ would be
View SolutionTwo forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
View SolutionA parallel plate capacitor is charged by certain amount of charge Q. The force of interaction between the plates is F0. If region between the plates is filled by a dielectric material, the force of interaction between the plates is F. The correct statement is
View Solution
