A simple electric motor has an armature resistance of 1Ω and runs from a dc source of 12 volt . When running unloaded it draws a current of 2 amp . When a certain load is connected , its speed becomes one-half of its unloaded value . The new value of current drawn
3A
6A
2A
1A
The correct Answer is:A
To solve the problem step by step, we need to analyze the given information and apply the relevant formulas.
Step 1: Identify the given values
- Armature resistance, Ra=1Ω
- Voltage from the DC source, V=12V
- Unloaded current, Iunloaded=2A
Step 2: Calculate the back emf when the motor is unloaded
The back emf (Vb) can be calculated using the formula:
Vb=V−I⋅Ra
Substituting the known values:
Vb=12V−(2A⋅1Ω)=12V−2V=10V
Step 3: Determine the new speed and back emf when the load is connected
When a load is connected, the speed of the motor becomes half of its unloaded speed. The back emf is proportional to the speed of the motor, so if the speed is halved, the back emf will also be halved:
Vb,new=12Vb=12⋅10V=5V
Step 4: Calculate the new current drawn with the load
Using the same formula for back emf:
Vb=V−Inew⋅Ra
We can rearrange this to solve for the new current (Inew):
Inew=V−VbRa
Substituting the values we have:
Inew=12V−5V1Ω=7V1Ω=7A
Step 5: Determine the total current drawn from the source
The total current drawn from the source when the load is connected is the sum of the unloaded current and the new current:
Itotal=Iunloaded+Inew=2A+7A=9A
Conclusion
The new value of the current drawn by the motor when a load is connected is 9 A.
- Armature resistance, Ra=1Ω
- Voltage from the DC source, V=12V
- Unloaded current, Iunloaded=2A
The back emf (Vb) can be calculated using the formula:
Vb=V−I⋅Ra
Substituting the known values:
Vb=12V−(2A⋅1Ω)=12V−2V=10V
When a load is connected, the speed of the motor becomes half of its unloaded speed. The back emf is proportional to the speed of the motor, so if the speed is halved, the back emf will also be halved:
Vb,new=12Vb=12⋅10V=5V
Using the same formula for back emf:
Vb=V−Inew⋅Ra
We can rearrange this to solve for the new current (Inew):
Inew=V−VbRa
Substituting the values we have:
Inew=12V−5V1Ω=7V1Ω=7A
The total current drawn from the source when the load is connected is the sum of the unloaded current and the new current:
Itotal=Iunloaded+Inew=2A+7A=9A
The new value of the current drawn by the motor when a load is connected is 9 A.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - B) (OBJECTIVE TYPE QUESTIONS)
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -C) Previous Years Questions
34 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
30 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
The resistance of an ammeter is 13Ω and its scale is graduated for a current upto 100A. After an additional shunt has been connected to this ammeter it becomes possible to measure currents upto 750A by this meter. The value of shunt resistance is
View SolutionA coil of inductance 300mh and resistance 2Ω is connected to a source of voltage 2V. The current reaches half of its steady state value in
View SolutionThe resistance of an ammeter of range 5A is 1.8Ω A shunt of 0.2Ω is connected in parallel to it. When its indicator shows a current of 2A then what will be effective current?
View SolutionIn the circuit shown in figure, the resistance R has a value that depends on the current. Specifically R is 20 Ω when i is zero and the amount of increase in resistance is numerically equal to one-half of the current. What is the value of current I in circuit?

View SolutionA resistance of 20Ω is connected to a source of alternating current rated 110V,50Hz. Find (a) the rms current, (b) the maximum instantaneous current in the resistor and (c) the time taken by the current to change from its maximum value to the rms value.
View SolutionThe armature of a DC motor has 20Ω resistance. It draws a current of 1.5A when run by 200VDC supply The value of back emf induced in it will be
View SolutionThe armature of a DC motor has 20Ω resistance. It draws a current of 1.5A when run by 200VDC supply The value of back emf induced in it will be
View SolutionA dc motor works on the principle that a current carrying coil, when placed in a magnetic field experiences a torque. The arrangement consists of a coil suspended in a region of magnetic field. When a current is passed through the coil, it experiences torque and starts rotating. A simple arrangement is shown below.
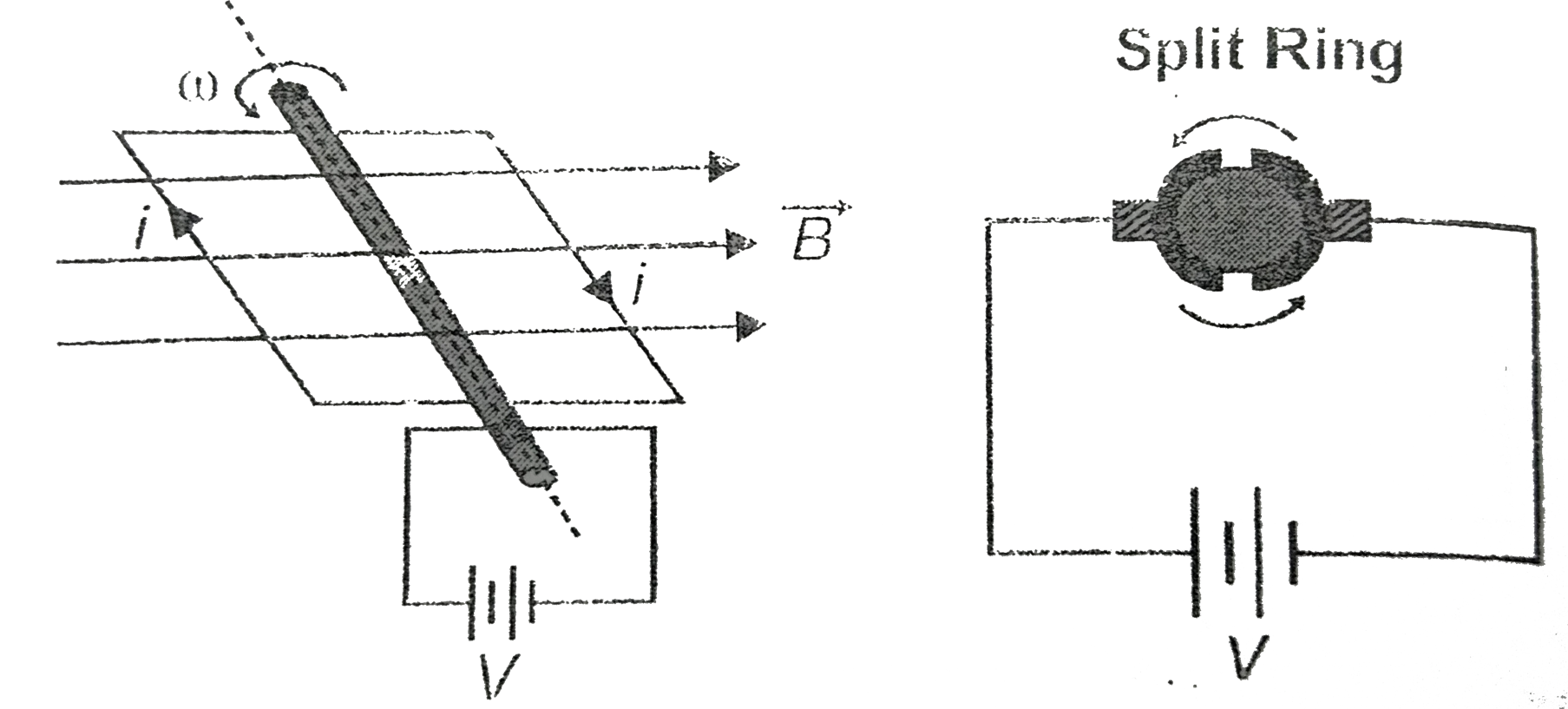
The coil rotates under the action of torque. The current is supplied to the coil by an arrangement of two sliding contacts and a split ring. As the coil rotates, the magnetic flux linked with the coil changes. This leads to production of an induced emf ε in the coil. By Lenz's law, the induced emf opposes the applied voltage and therefore, it is called back emf. If R is the resistance in the coil, the current i flowing through the coil at any instant is i=V−εR. The back emf is developed due to induction and it is directly proportional to speed of rotation and it is directly proportional to speed of rotation of the motor. There is a continuous power loss i2R in the motor, in form of heat.
When a dc motor is running unloaded (full speed) the current through it is 1 A. What will be the current flowing through the motor, when it is loaded to run at half its maximum speed, it applied voltage is 10 V and armature resistance is 5Ω
View Solutionthe current developed in a real conductor is given I=aV1/2, where V is the potential difference acid the conductor. When it is connected with resistance of RΩ in series with a battery of 6 volt shown in the figure , the power developed in conductor is twice the power generated in resistance of RΩ . find the value of R.[a=0.2AVolt−1/2]
View SolutionA series LCR circuit with a resistance of 100√5Ω is connected to an ac source of 200 V. When the capacitor is removed from the circuit, current lags behind emf by 45∘. When the inductor is removed from the circuit keeping the capacitor and resistor in the circuit, current leads by an angle of tan−1(12). Calculate the current and power dissipated in LCR circuit.
View Solution
