A: When the magnetic flux through a loop is maximum, induced emf is maximum.
R: When the magnetic flux through a loop is minimum, induced emf is minimum.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion.
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion.
If Assertion is true statement but Reason is false.
If both Assertion and Reason are false statements.
The correct Answer is:D
To solve the assertion-reason question, we need to analyze both statements carefully.
Step 1: Understanding the Assertion
The assertion states: "When the magnetic flux through a loop is maximum, induced emf is maximum."
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes, along with the cosine of the angle (θ) between the field and the normal to the surface.
- The induced electromotive force (emf) in a loop is given by Faraday's law of electromagnetic induction, which states that the induced emf (ε) is equal to the rate of change of magnetic flux through the loop:
ϵ=−dΦdt
- If the magnetic flux is at a maximum, it means that there is no change in flux at that instant (dΦ/dt = 0), which implies that the induced emf is zero.
Step 2: Understanding the Reason
The reason states: "When the magnetic flux through a loop is minimum, induced emf is minimum."
- Similar to the assertion, if the magnetic flux is at a minimum, it also indicates that there is no change in flux at that instant (dΦ/dt = 0), leading to an induced emf of zero.
Step 3: Conclusion
Both the assertion and the reason are false because:
- When the magnetic flux is at a maximum, the induced emf is zero (not maximum).
- When the magnetic flux is at a minimum, the induced emf is also zero (not minimum).
Thus, the correct answer is that both the assertion and reason are false.
Final Answer
Both Assertion (A) and Reason (R) are false.
---
The assertion states: "When the magnetic flux through a loop is maximum, induced emf is maximum."
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes, along with the cosine of the angle (θ) between the field and the normal to the surface.
- The induced electromotive force (emf) in a loop is given by Faraday's law of electromagnetic induction, which states that the induced emf (ε) is equal to the rate of change of magnetic flux through the loop:
ϵ=−dΦdt
- If the magnetic flux is at a maximum, it means that there is no change in flux at that instant (dΦ/dt = 0), which implies that the induced emf is zero.
The reason states: "When the magnetic flux through a loop is minimum, induced emf is minimum."
- Similar to the assertion, if the magnetic flux is at a minimum, it also indicates that there is no change in flux at that instant (dΦ/dt = 0), leading to an induced emf of zero.
Both the assertion and the reason are false because:
- When the magnetic flux is at a maximum, the induced emf is zero (not maximum).
- When the magnetic flux is at a minimum, the induced emf is also zero (not minimum).
Both Assertion (A) and Reason (R) are false.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -C) Previous Years Questions
Explore 34 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:comprehension
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
Similar Questions
Which of the following can produce maximum induced emf?
View SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . Which of the following option is correct

View SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . What is relation between them

View SolutionThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
View Solution(A): Only a change in magnetic flux will maintain an induced current in the coil.
(R): The presence of large magnetic flux through a coil maintains a current in the coil if the circuit is continuous
View SolutionA wire of linear charge density λ passes through a cuboid of length l, breadth b and height h(l>b>h) in such a manner that the flux through the cuboid is maximum. The position of the wire is now changed, so that the flux through the cuboid is minimum. The raito of maximum flux to minimum flux will be
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
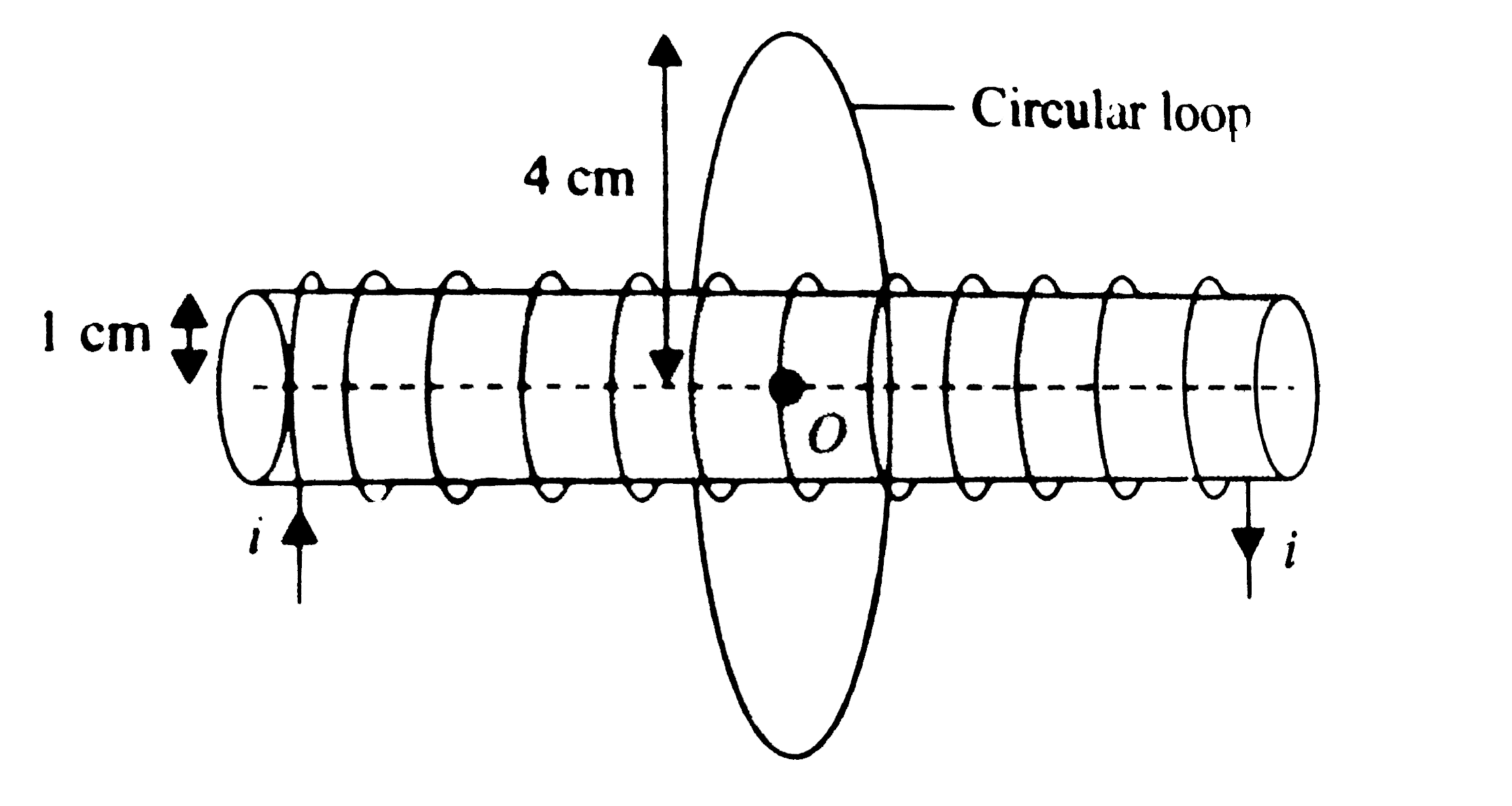
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View SolutionWhenever the magnet flux linked with a coil changes, then is an induced emf in the circuit. This emf lasts
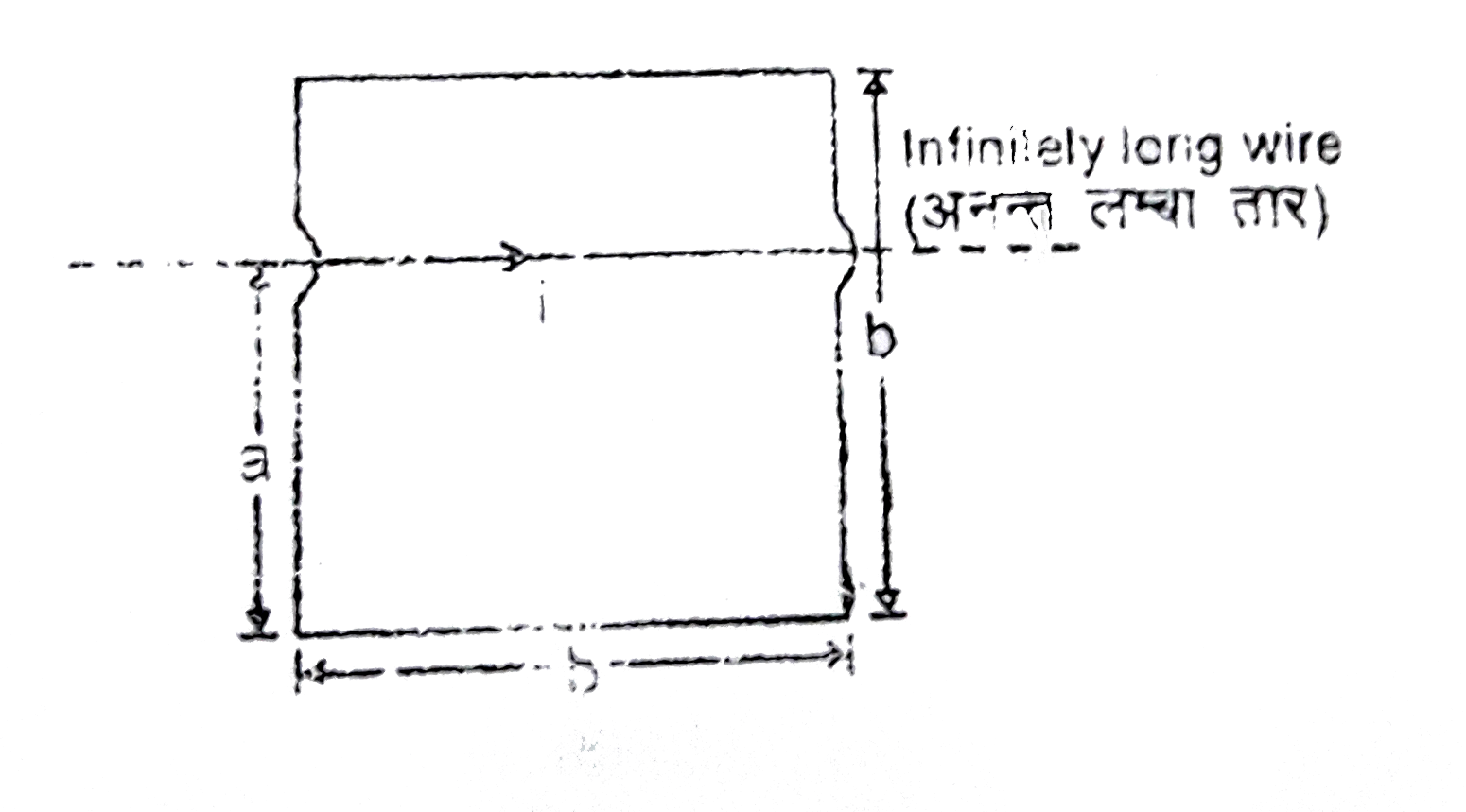
View SolutionFor the situation shown in the figure, flux through the square loop is:
View Solution
