An a.c. of frequency f is flowing in a circuit containing only an ideal choke coil of inductance L. If V0andl0 represent peak values of the voltage and the current respectively. The average power given by the source to the choke coil is equal to
12l0V0
12l20(2πfL)
Zero
12V0(2πfL)
The correct Answer is:C
To solve the problem, we need to determine the average power delivered to an ideal choke coil (inductor) in an AC circuit. The key points to consider are the relationships between voltage, current, and power in an inductive circuit.
1. Understand the Circuit:
The circuit consists of an ideal choke coil (inductor) with inductance L and an alternating current (AC) of frequency f flowing through it.
2. Identify Peak Values:
Let V0 be the peak voltage across the inductor and I0 be the peak current through the inductor.
3. Convert Peak Values to RMS Values:
The root mean square (RMS) values of voltage and current can be calculated from their peak values:
Vrms=V0√2andIrms=I0√2
4. Determine the Phase Angle:
In an ideal inductor, the current lags the voltage by 90∘ (or π2 radians). Therefore, the power factor cosϕ is:
cosϕ=cos(π2)=0
5. Calculate Average Power:
The average power P delivered to the inductor can be calculated using the formula:
P=Vrms⋅Irms⋅cosϕ
Substituting the values we found:
P=(V0√2)⋅(I0√2)⋅0
Simplifying this gives:
P=0
Conclusion:
The average power given by the source to the choke coil is equal to 0.
The circuit consists of an ideal choke coil (inductor) with inductance L and an alternating current (AC) of frequency f flowing through it.
Let V0 be the peak voltage across the inductor and I0 be the peak current through the inductor.
The root mean square (RMS) values of voltage and current can be calculated from their peak values:
Vrms=V0√2andIrms=I0√2
In an ideal inductor, the current lags the voltage by 90∘ (or π2 radians). Therefore, the power factor cosϕ is:
cosϕ=cos(π2)=0
The average power P delivered to the inductor can be calculated using the formula:
P=Vrms⋅Irms⋅cosϕ
Substituting the values we found:
P=(V0√2)⋅(I0√2)⋅0
Simplifying this gives:
P=0
The average power given by the source to the choke coil is equal to 0.
Similar Questions
In an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
View SolutionA circuit contains resistance R and an inductance L in series. An alternating voltage V=V0sinωt is applied across it. The currents in R and L respectively will be
 .
.
View SolutionA circuit contains resistance R and an inductance L in series. An alternating voltage V=V0sinωt is applied across it. The currents in R and L respectively will be
 .
.
View SolutionA choke coil of resistance R and inductance is connected to an ac. source of frequency f and peak voltage V If angular frequency will increase then, the average power dissipated in the choke
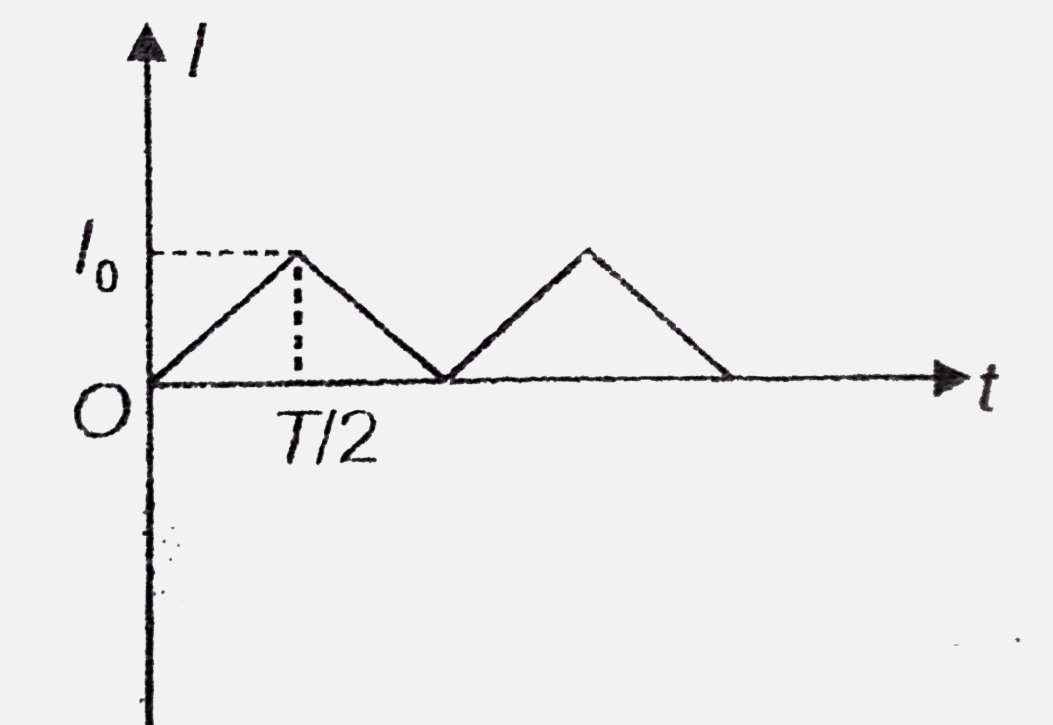
View SolutionThe current in a certain circuit varies with time as shown. The peak value of current is l0 . If ivandim represent the virtual (rms) and mean value of current for a complete cycle respectively, then
View SolutionA closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionA closed circuit consists of a source of constant emfE and a choke coil of inductance L connected in series.The active resistance of the whole circuit is equal to R.It is in steady state.At the moment L=0 the choke coil inductance was decreased abruptly 4 times.The current in the circuit as a function of time t is ER[1−xc−4tR/L].Find out value of x.
View SolutionThe circuit given in fig. has a resistanceless choke coil L and a resistance R. The voltage across R and L are also given in the figure. The virtual value of the applied voltage is

View SolutionA coil of inductance 5.0 mH and negligible resistance is connected to an alternating voltage V=10sin(100t). The peak current in the circuit will be:
View SolutionIf V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
View Solution
