When a voltage V=V0 cos ωt is applied across a resistor of resistance R, the average power dissipated per cycle in the resistor is given by
V0√2R
V0√2ωR
V202R
V202ωR
The correct Answer is:C
To find the average power dissipated per cycle in a resistor when a voltage V=V0cos(ωt) is applied, we can follow these steps:
1. Identify the Voltage and Current:
The voltage across the resistor is given by:
V(t)=V0cos(ωt)
The current I(t) through the resistor R can be calculated using Ohm's law:
I(t)=V(t)R=V0cos(ωt)R
2. Calculate Instantaneous Power:
The instantaneous power P(t) dissipated in the resistor is given by:
P(t)=V(t)⋅I(t)=V0cos(ωt)⋅V0cos(ωt)R=V20cos2(ωt)R
3. Average Power Over One Cycle:
To find the average power Pavg over one complete cycle, we need to integrate P(t) over one period T and then divide by T:
Pavg=1T∫T0P(t)dt=1T∫T0V20cos2(ωt)Rdt
4. Substituting the Period:
The period T of the cosine function is given by:
T=2πω
Thus, we can substitute T into the average power equation:
Pavg=12πω∫2πω0V20cos2(ωt)Rdt
5. Using the Identity for Cosine Squared:
We can use the trigonometric identity:
cos2(θ)=1+cos(2θ)2
Therefore:
P(t)=V20R⋅1+cos(2ωt)2
6. Integrating:
Now we can integrate:
Pavg=12πω∫2πω0V202R(1+cos(2ωt))dt
The integral of cos(2ωt) over one complete cycle is zero, so we only need to integrate the constant term:
Pavg=12πω⋅V202R⋅∫2πω01dt
The integral of 1 over the period T is simply T:
Pavg=12πω⋅V202R⋅2πω
7. Final Simplification:
This simplifies to:
Pavg=V202R
Conclusion:
The average power dissipated per cycle in the resistor is:
Pavg=V202R
The voltage across the resistor is given by:
V(t)=V0cos(ωt)
The current I(t) through the resistor R can be calculated using Ohm's law:
I(t)=V(t)R=V0cos(ωt)R
The instantaneous power P(t) dissipated in the resistor is given by:
P(t)=V(t)⋅I(t)=V0cos(ωt)⋅V0cos(ωt)R=V20cos2(ωt)R
To find the average power Pavg over one complete cycle, we need to integrate P(t) over one period T and then divide by T:
Pavg=1T∫T0P(t)dt=1T∫T0V20cos2(ωt)Rdt
The period T of the cosine function is given by:
T=2πω
Thus, we can substitute T into the average power equation:
Pavg=12πω∫2πω0V20cos2(ωt)Rdt
We can use the trigonometric identity:
cos2(θ)=1+cos(2θ)2
Therefore:
P(t)=V20R⋅1+cos(2ωt)2
Now we can integrate:
Pavg=12πω∫2πω0V202R(1+cos(2ωt))dt
The integral of cos(2ωt) over one complete cycle is zero, so we only need to integrate the constant term:
Pavg=12πω⋅V202R⋅∫2πω01dt
The integral of 1 over the period T is simply T:
Pavg=12πω⋅V202R⋅2πω
This simplifies to:
Pavg=V202R
The average power dissipated per cycle in the resistor is:
Pavg=V202R
Similar Questions
A voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View SolutionIn the circuit shown, the average power dissipated in the resistor is (assume diode to be ideal)
View Solution
Knowledge Check
An alternating supply of 220 V is applied across a circuit with resistance 22Ω and impedance 44Ω. The power dissipated in the circuit is
A1100 WB550 WC2200 WD(2200/3) W
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionAn alternating voltage V=140 sin 50 t is applied to a resistor of resistance 10 Ω. This voltage produces △H heat in the resistor in time △t. To produce the same heat in the same time, rquired DC current is
View SolutionAn alternating voltage V=140 sin 50 t is applied to a resistor of resistance 10 Ω. This voltage produces △H heat in the resistor in time △t. To produce the same heat in the same time, rquired DC current is
View SolutionA circuit is set up by connecting L=100mH, C=5μF and R=100Ω in series. An alternating emf of 150√2 )V,(500)/(pi) Hz is applied across this series combination.Calculate the impedance of the circuit. What is the average power dissipated in the resistor
View SolutionThe values of current (I) flowng through a given resistor of resistance (R ), for the corresponding values of potential difference (V) across the resistor are as given below :

Plot a graph between current (I) and potential difference (V) and determine the resistance (R ) of the resistor.
View Solution220 V, 50 Hz , AC is applied to a resistor . The instantaneous value of voltage is
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
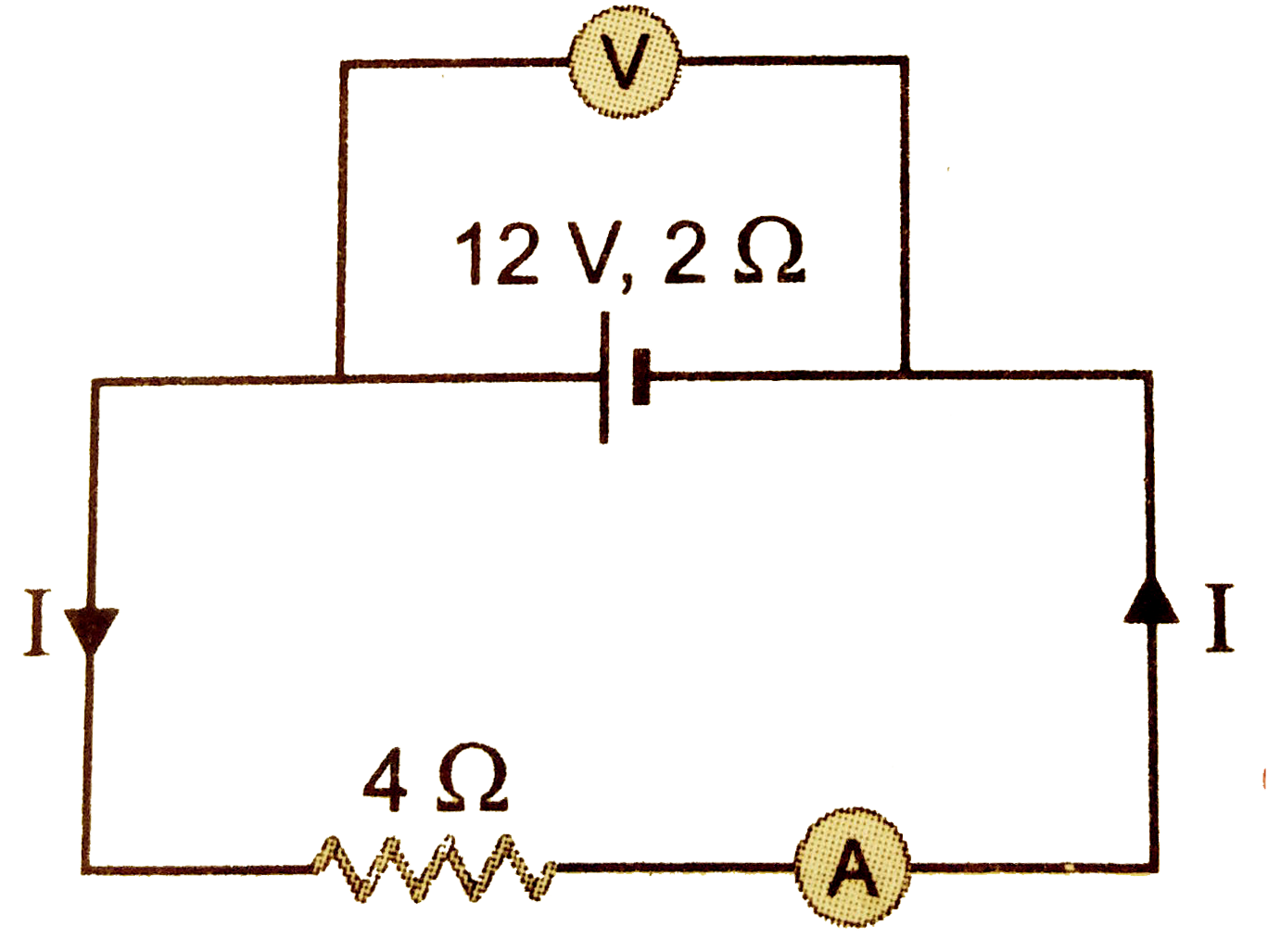
View Solution
