In the circuit shown, the average power dissipated in the resistor is (assume diode to be ideal)
E202R
E204R
E20R
Zero
The correct Answer is:B
To find the average power dissipated in the resistor in the given circuit with an ideal diode, we can follow these steps:
Step 1: Understand the Circuit
The circuit consists of an ideal diode (D1) in series with a resistor (R), connected to an AC voltage source V(t)=V0sin(ωt). The diode will only allow current to flow in one direction, effectively clipping the negative half of the AC waveform.
Step 2: Determine the Current through the Resistor
For an ideal diode, the current through the resistor when the diode is forward-biased (i.e., during the positive half-cycle of the AC signal) can be expressed as:
I(t)=V(t)R=V0sin(ωt)R
for 0≤ωt≤π (the positive half-cycle).
Step 3: Calculate the Average Power without the Diode
The average power Pavg dissipated in the resistor without the diode can be calculated using the formula:
Pavg=1T∫T0V2(t)dt
where T is the period of the AC signal. The average power without the diode (considering the full cycle) is:
Pavg, without diode=12⋅V20R
This is because the average of sin2(ωt) over one complete cycle is 12.
Step 4: Calculate the Average Power with the Diode
Since the diode only allows current during the positive half-cycle, the average power dissipated in the resistor with the diode can be given by:
Pavg, with diode=12⋅Pavg, without diode=12⋅(12⋅V20R)=14⋅V20R
Step 5: Final Expression for Average Power
Thus, the average power dissipated in the resistor when the diode is ideal is:
P=V204R
Conclusion
The average power dissipated in the resistor is V204R.
The circuit consists of an ideal diode (D1) in series with a resistor (R), connected to an AC voltage source V(t)=V0sin(ωt). The diode will only allow current to flow in one direction, effectively clipping the negative half of the AC waveform.
For an ideal diode, the current through the resistor when the diode is forward-biased (i.e., during the positive half-cycle of the AC signal) can be expressed as:
I(t)=V(t)R=V0sin(ωt)R
for 0≤ωt≤π (the positive half-cycle).
The average power Pavg dissipated in the resistor without the diode can be calculated using the formula:
Pavg=1T∫T0V2(t)dt
where T is the period of the AC signal. The average power without the diode (considering the full cycle) is:
Pavg, without diode=12⋅V20R
This is because the average of sin2(ωt) over one complete cycle is 12.
Since the diode only allows current during the positive half-cycle, the average power dissipated in the resistor with the diode can be given by:
Pavg, with diode=12⋅Pavg, without diode=12⋅(12⋅V20R)=14⋅V20R
Thus, the average power dissipated in the resistor when the diode is ideal is:
P=V204R
The average power dissipated in the resistor is V204R.
Topper's Solved these Questions
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment section -C (Previous years type question)
110 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment section -A (Objective Type Question)
43 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - D)
16 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
Similar Questions
Knowledge Check
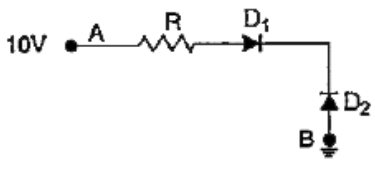
In figure , assuming the diodes to be ideal ,
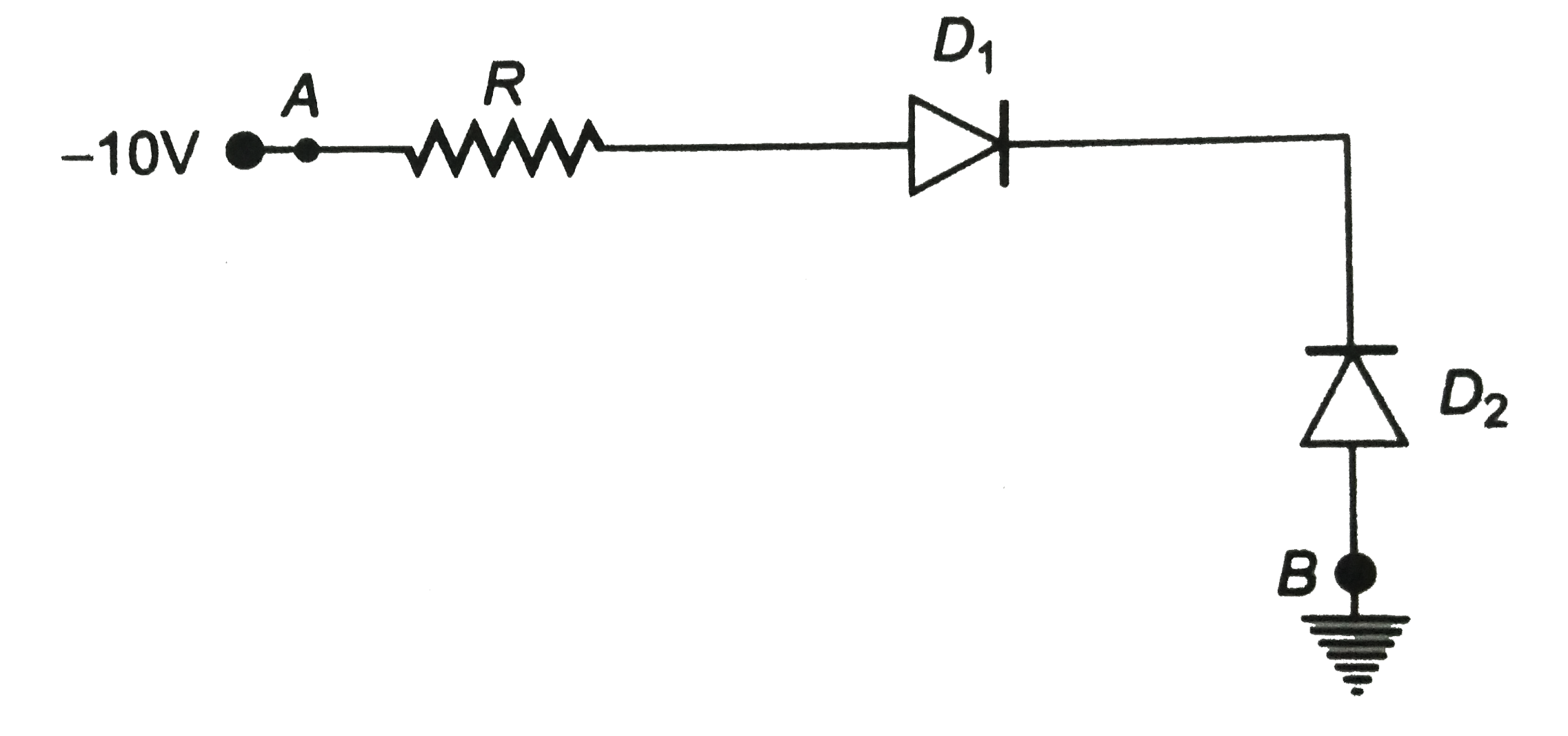 AD1 is forward biased and D2 is reverse biased and hence current flows from A to B.BD2 is forward biased and D1 is reverse biased and hence no current flows from B to A and vice versa.CD1andD2 are both forward biased and hence current flows from A to B.DD1andD2 are both reverse biased and hence no current flows from A to B and vice versa
AD1 is forward biased and D2 is reverse biased and hence current flows from A to B.BD2 is forward biased and D1 is reverse biased and hence no current flows from B to A and vice versa.CD1andD2 are both forward biased and hence current flows from A to B.DD1andD2 are both reverse biased and hence no current flows from A to B and vice versa
In the given circuit the average power developed is:
View SolutionThe power dissipated in the adjacent circuit is -
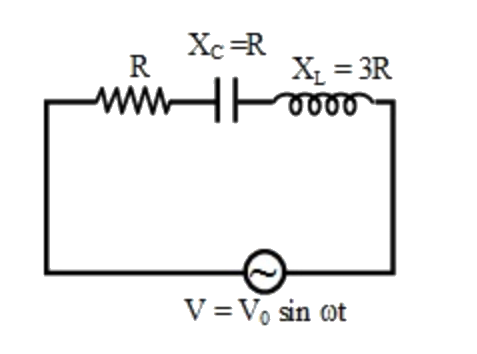
View SolutionIn figure , assuming the diodes to be ideal ,

View SolutionIn figure , assuming the diodes to be ideal ,

View SolutionIn the circuit shown, the resistance are given ohms and the battery is assumed ideal with end equal to 3.0 volts. The resistance that dissipates the maximum power is
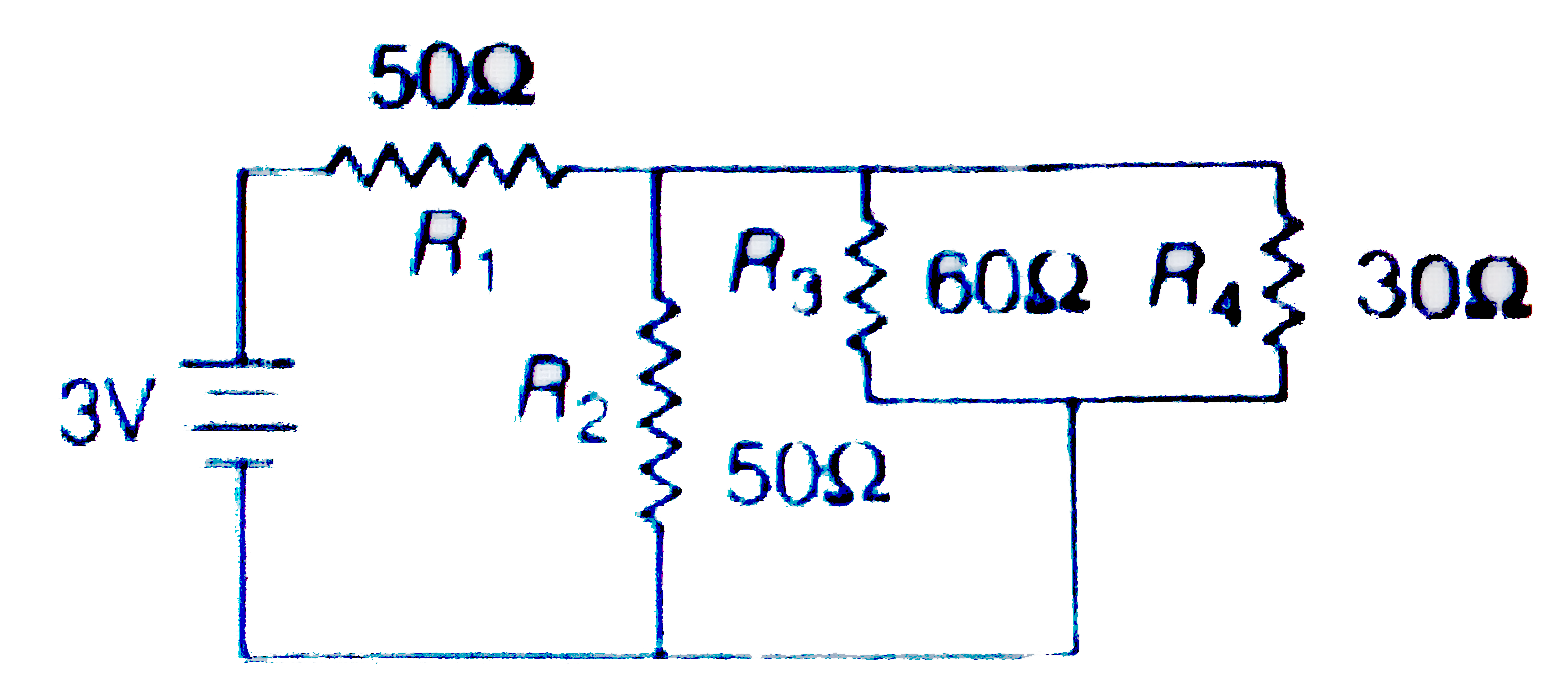
View SolutionIn figure, assuming the diodes to be ideal,
View SolutionAssume that the batteries in figure have negligible internal resistance. Find
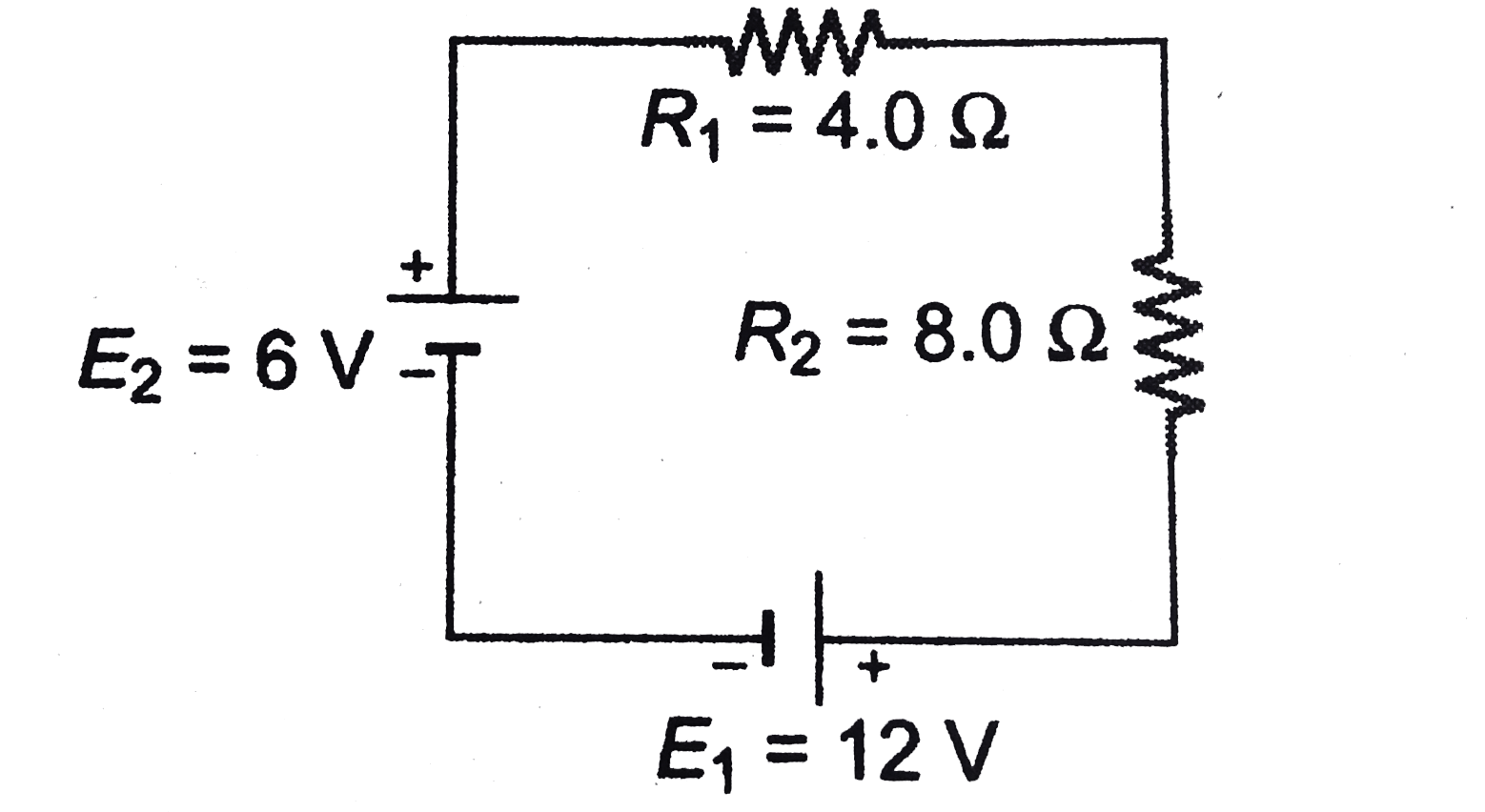
a. the current in the circuit,
(b) the power dissipated in each resistor and
(c) the power of each battery, stating whether energy is supplied by or absorbed by it
View Solution