You have two copper cables of equal length for carrying current. One of them has a single wire of area of across section A, the other has ten wires each of cross section area A/10. Judge their suitability for transporting ac and dc.
Only multiple strands for A.C. either for D.C.
Only mutiple stands for A.C, only single strand for D.C.
Only single strand for D.C. either for A.C.
Only single strand for A.C, either for D.C.
The correct Answer is:A
To determine the suitability of two copper cables for transporting AC and DC, we will analyze their resistances and surface areas.
1. Identify the Cables:
- Cable 1: A single wire with a cross-sectional area A.
- Cable 2: Ten wires, each with a cross-sectional area A10.
2. Calculate Resistance for DC:
- The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity of the material and L is the length of the wire.
- For Cable 1:
R1=ρLA
- For Cable 2, since there are 10 parallel wires, we first calculate the resistance of one wire:
Rsingle=ρLA10=10ρLA
Since they are in parallel, the equivalent resistance Req is given by:
1Req=1Rsingle+1Rsingle+…+1Rsingle(10 times)
1Req=10⋅A10ρL=AρL
Thus,
Req=ρLA
3. Comparison of Resistances:
- Both cables have the same resistance R1=Req=ρLA.
- Therefore, both cables are equally suitable for transporting DC current.
4. Calculate Surface Area for AC:
- For AC current, the effective surface area of the wire is important since AC tends to travel on the surface of conductors.
- The surface area S of a cylindrical wire is given by:
S=2πrh
where r is the radius and h is the length.
- For Cable 1:
- The radius r1 can be calculated from the area A:
r1=√Aπ
Therefore, the surface area S1 is:
S1=2π(√Aπ)L=2L√Aπ
- For Cable 2:
- Each wire has a radius r2=√A/10π.
- The surface area of one wire is:
Ssingle=2π⎛⎝√A/10π⎞⎠L=2L√A10π
- Since there are 10 wires:
S2=10⋅Ssingle=10⋅2L√A10π=2L√10Aπ
5. Comparison of Surface Areas:
- Comparing S1 and S2:
S2=2L√10AπandS1=2L√Aπ
- Clearly, S2 is greater than S1 since √10>1.
6. Conclusion:
- For DC, both cables are equally suitable as they have the same resistance.
- For AC, the cable with multiple strands (Cable 2) is more suitable due to its larger surface area.
Final Answer:
- Both cables are suitable for DC.
- The cable with multiple strands (Cable 2) is more suitable for AC.
- Cable 1: A single wire with a cross-sectional area A.
- Cable 2: Ten wires, each with a cross-sectional area A10.
- The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity of the material and L is the length of the wire.
- For Cable 1:
R1=ρLA
- For Cable 2, since there are 10 parallel wires, we first calculate the resistance of one wire:
Rsingle=ρLA10=10ρLA
Since they are in parallel, the equivalent resistance Req is given by:
1Req=1Rsingle+1Rsingle+…+1Rsingle(10 times)
1Req=10⋅A10ρL=AρL
Thus,
Req=ρLA
- Both cables have the same resistance R1=Req=ρLA.
- Therefore, both cables are equally suitable for transporting DC current.
- For AC current, the effective surface area of the wire is important since AC tends to travel on the surface of conductors.
- The surface area S of a cylindrical wire is given by:
S=2πrh
where r is the radius and h is the length.
- For Cable 1:
- The radius r1 can be calculated from the area A:
r1=√Aπ
Therefore, the surface area S1 is:
S1=2π(√Aπ)L=2L√Aπ
- Each wire has a radius r2=√A/10π.
- The surface area of one wire is:
Ssingle=2π⎛⎝√A/10π⎞⎠L=2L√A10π
- Since there are 10 wires:
S2=10⋅Ssingle=10⋅2L√A10π=2L√10Aπ
- Comparing S1 and S2:
S2=2L√10AπandS1=2L√Aπ
- Clearly, S2 is greater than S1 since √10>1.
- For DC, both cables are equally suitable as they have the same resistance.
- For AC, the cable with multiple strands (Cable 2) is more suitable due to its larger surface area.
- Both cables are suitable for DC.
- The cable with multiple strands (Cable 2) is more suitable for AC.
Similar Questions
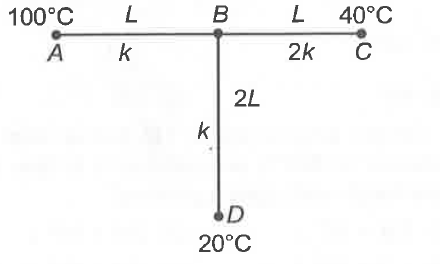
Find the temperature of junction at B, if each rod has equal area of cross-section.
View SolutionA light rod of length 2m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section 0.1cm2. The other wire is a brass of cross section 0.2cm2. A weight is suspended from a certain point of the rod such that equal stress are produced in both the wires. Which of the following are correct?
View Solution
Knowledge Check
A light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
Two wires of the same materical having equal area of cross-section have L and 2L. Their respective resistances are in the ratio
View SolutionA homogeneous block with a mass m hangs on three vertical wires of equal length arranged symmetrically . Find the tensions of the wires if the middle wire is of steel and the other two are of copper . All the wires have the same cross - section . Consider the modulus of elasticity of steel to be double than that of copper .

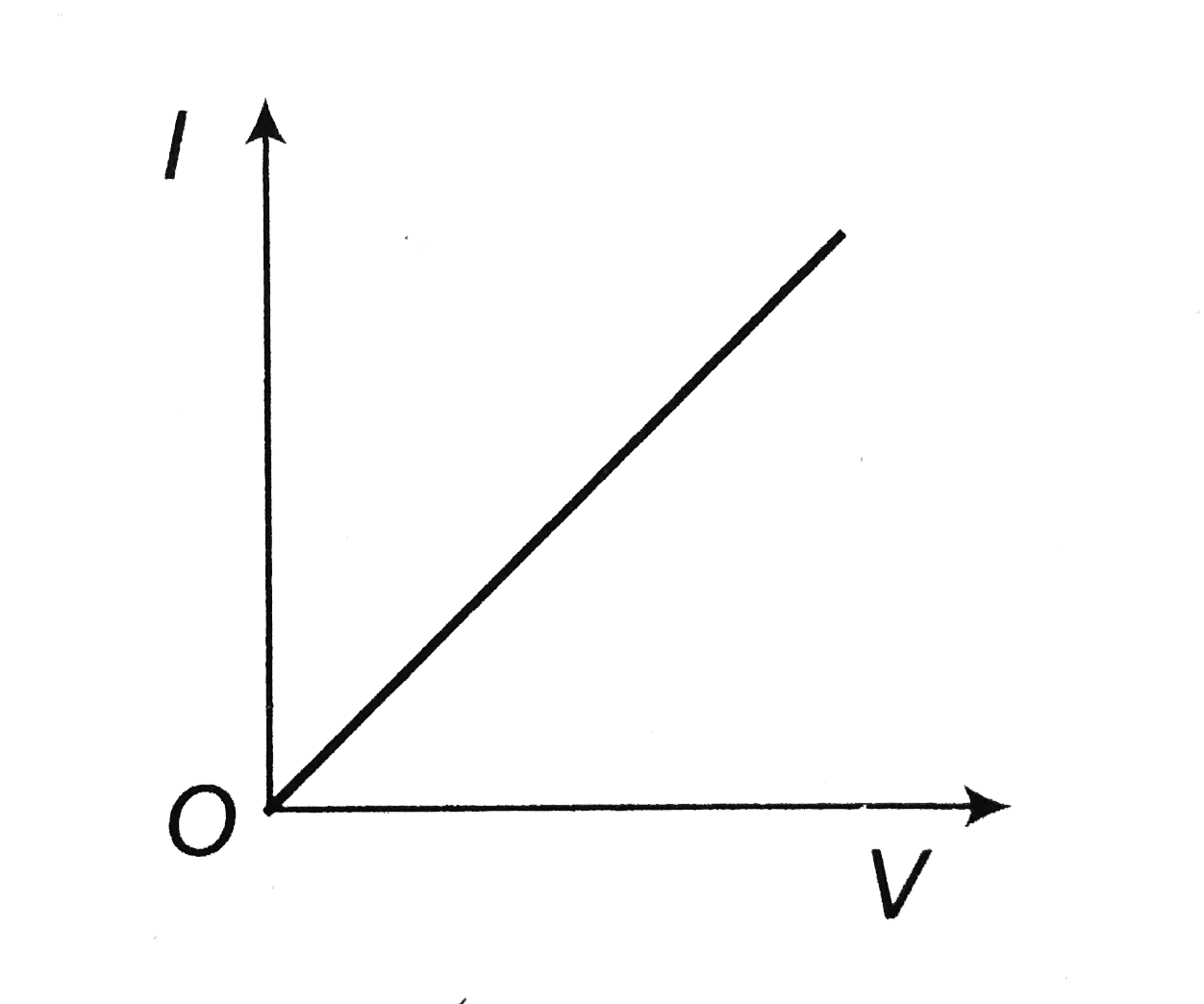
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
View SolutionTwo wires of equal length one of copper and other of manganin have the same resistance. Which wire is thicker?
View SolutionTwo solid conductors are made up of same material have same length and same resistance . One of them has circular crosssection of area A1 and other one has square cross section of area A2. RATIO A1A2
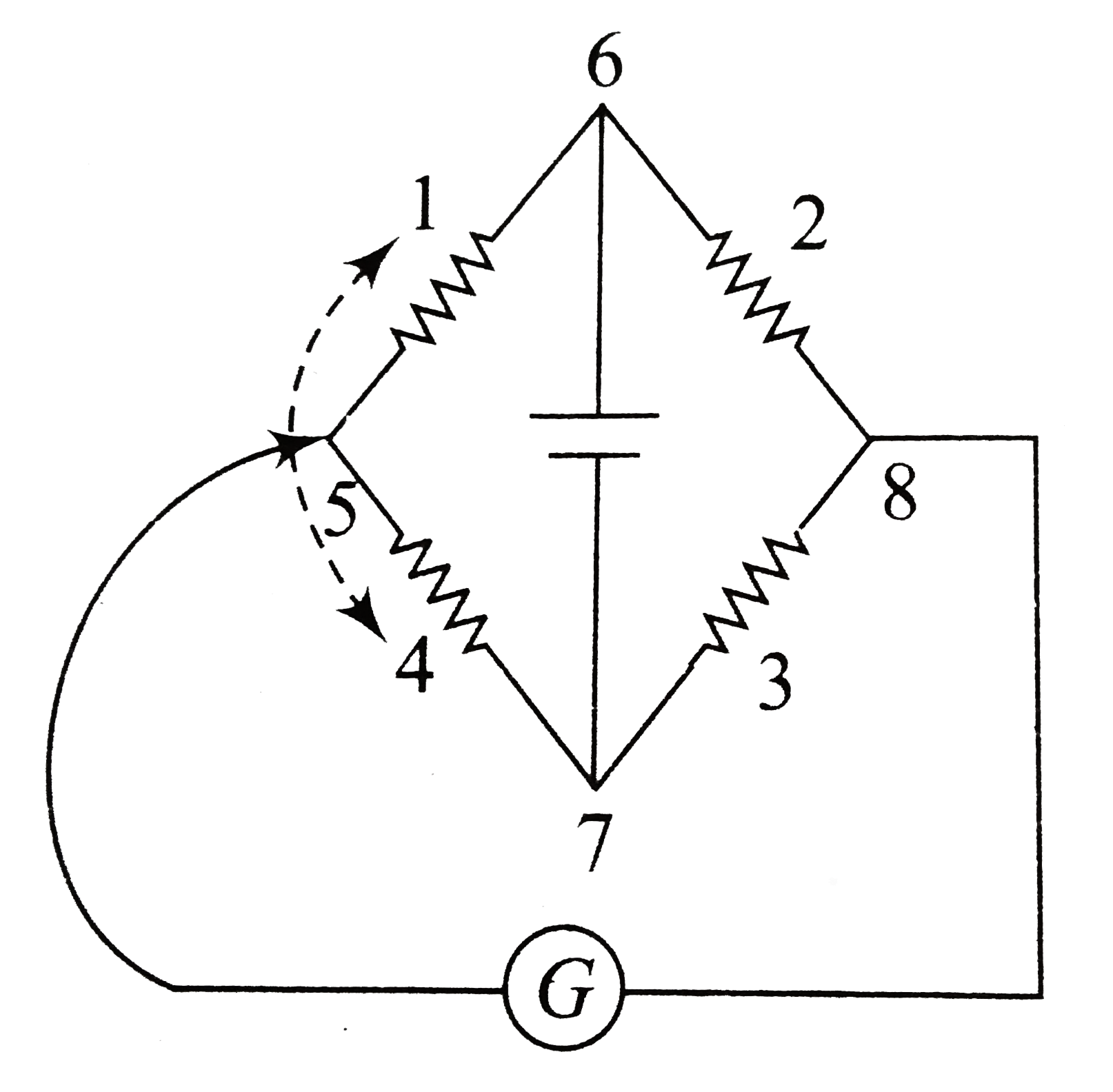
View SolutionFour wires of equal length 2 m are arranged as shown in the figure. Wires , 2, 3 and 4 are of equal cross-sectional area and wire 1 is of half the cross section of these wires. By how much distance pointer at point 5 must be moved to get null point ?
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View Solution
