In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.17 sec. The frequency of the wave is
0.73 Hz
0.36 Hz
1.47 Hz
2.94 Hz
The correct Answer is:C
Step by step video & image solution for In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.17 sec. The frequency of the wave is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-C ( Previous year Questions ))
53 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-A ( Objective type Questions ))
50 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
Similar Questions
In a sinusoidal wave the time required for a particular point to move from equilibrium position to maximum displacement is 0.17s, then the frequency of wave is:
View SolutionWhen a sound wave of frequency 300 Hz passes through a medium the maximum displacement of a particle of the medium is 0.1 cm . The maximum velocity of the particle is equal to
View SolutionIf the number of waves from a source is passing a point is 30 in a second, what is the frequency of the wave?
View SolutionA string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is 100k then find the value of k.
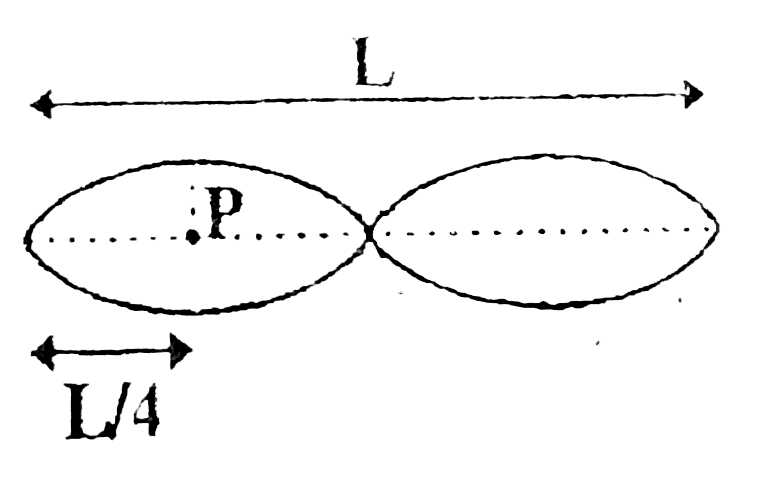
View SolutionA string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
View SolutionA sine wave is travelling in a medium. A particular partile has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
View SolutionA travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
View SolutionShows the shape of a progressive wave at time t=0. after a time t=(1)/(80), the particle at the origin has its maximum negative displacement.if the wave speed is 80 units maximum negative displacement. If the wave speed is 80 units, then find the equation of the progressive wave.
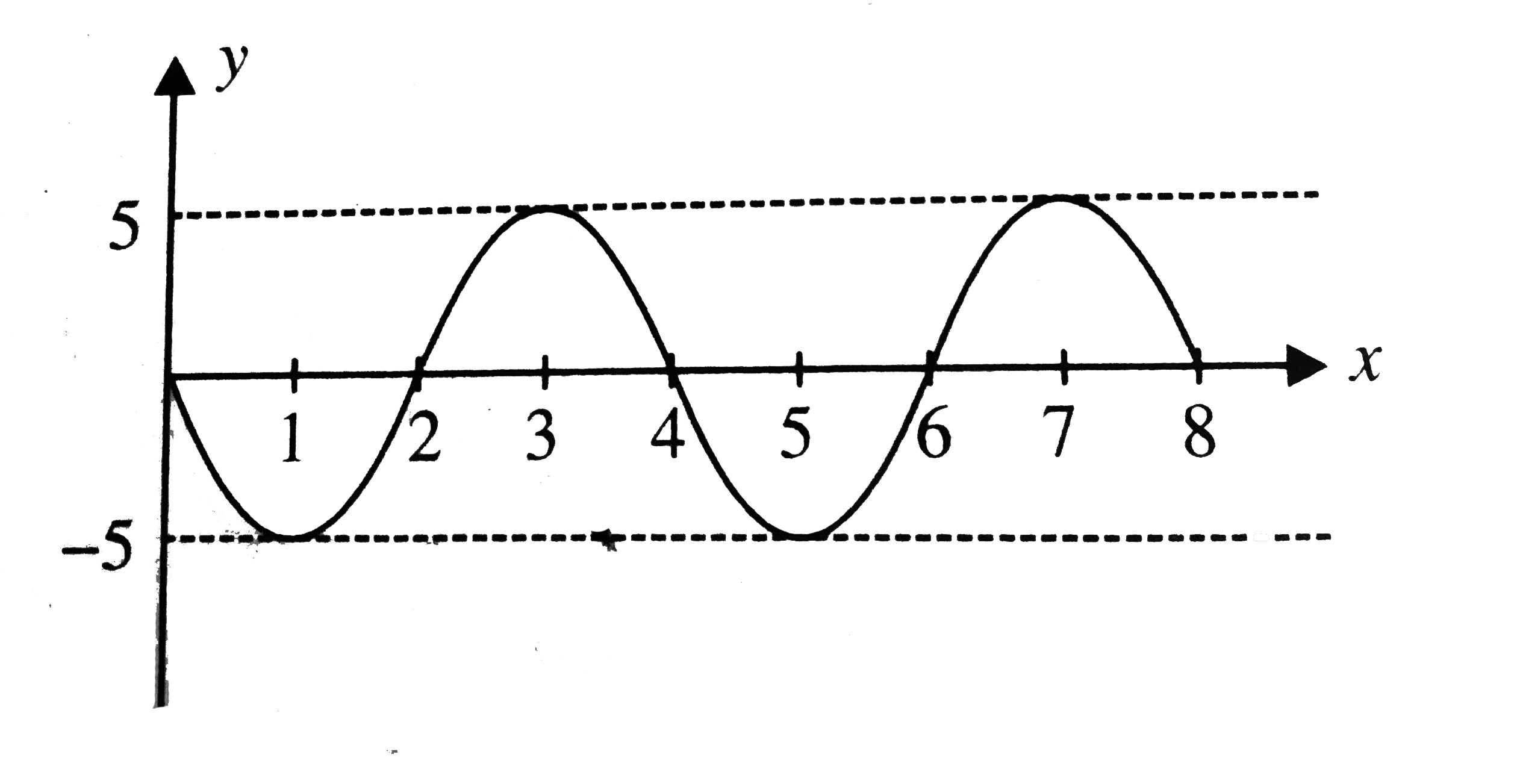 .
.
View SolutionAssertion : In longitudinal wave pressure is maximum at a point where displacement is zero .
Reason : There is a phase difference of π2 between y(x,t) and ΔP(x,t) equation in case of longitudinal wave.
View SolutionThe equation of a wave travelling on a string is y=(0.10mm)sin[3.14m−1)x+(314s−1)t]. (a) In which direction does the wave travel ? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string ?
View Solution
