The resultant resistance value of n resistance each of r ohms and connected is series is X. When those n , resistance are connected in parallel , the resultant values is .
xn
xn2
n2x
nx
The correct Answer is:B
To solve the problem, we need to find the resultant resistance when n resistors, each of resistance r ohms, are connected in series and then in parallel.
1. Understanding Series Connection:
When n resistors are connected in series, the total or equivalent resistance (X) is the sum of the individual resistances.
X=R1+R2+R3+...+Rn=nR
Here, since each resistor has the same resistance r, we can write:
X=nR
2. Finding Resistance (r):
From the equation X=nR, we can express R in terms of X and n:
R=Xn
This is our Equation 1.
3. Understanding Parallel Connection:
When the same n resistors are connected in parallel, the formula for the equivalent resistance Req is given by:
1Req=1R1+1R2+1R3+...+1Rn
Since all resistors have the same resistance R:
1Req=1R+1R+1R+...+1R=nR
Thus, we can write:
Req=Rn
4. Substituting for R:
Now, substituting R from Equation 1 into the parallel resistance formula:
Req=Xnn=Xn2
5. Final Result:
Therefore, the resultant resistance when the n resistors are connected in parallel is:
Req=Xn2
Conclusion:
The resultant resistance when n resistors of r ohms each are connected in parallel is Xn2.
When n resistors are connected in series, the total or equivalent resistance (X) is the sum of the individual resistances.
X=R1+R2+R3+...+Rn=nR
Here, since each resistor has the same resistance r, we can write:
X=nR
From the equation X=nR, we can express R in terms of X and n:
R=Xn
This is our Equation 1.
When the same n resistors are connected in parallel, the formula for the equivalent resistance Req is given by:
1Req=1R1+1R2+1R3+...+1Rn
Since all resistors have the same resistance R:
1Req=1R+1R+1R+...+1R=nR
Thus, we can write:
Req=Rn
Now, substituting R from Equation 1 into the parallel resistance formula:
Req=Xnn=Xn2
Therefore, the resultant resistance when the n resistors are connected in parallel is:
Req=Xn2
The resultant resistance when n resistors of r ohms each are connected in parallel is Xn2.
Similar Questions
A set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View SolutionThe resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance.
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionThe resultant resistance of two resistance in series is 50 Ω and it is 12 Ω , when they are in parallel. The individual resistances are
View SolutionTwo batteries (connected in series) of same emf 10 V of internal resistances 20ohm and 5ohm are connected to a load resistance of 30ohm. Now an unknown resistance x is connected in parallel to the load resistance. Find value of x so that potential drop of battery having internal resistance 20ohm becomes zero.
View SolutionThe resistance of the wire is 121 ohm. It is divided into .n. equal parts and they are connected in parallel, then effective resistance is 1 ohm. The value of .n. is
View SolutionThirteen resistances each of resistance R ohm are connected in the circuit as shown in the figure below. The effective resistance between A and B is
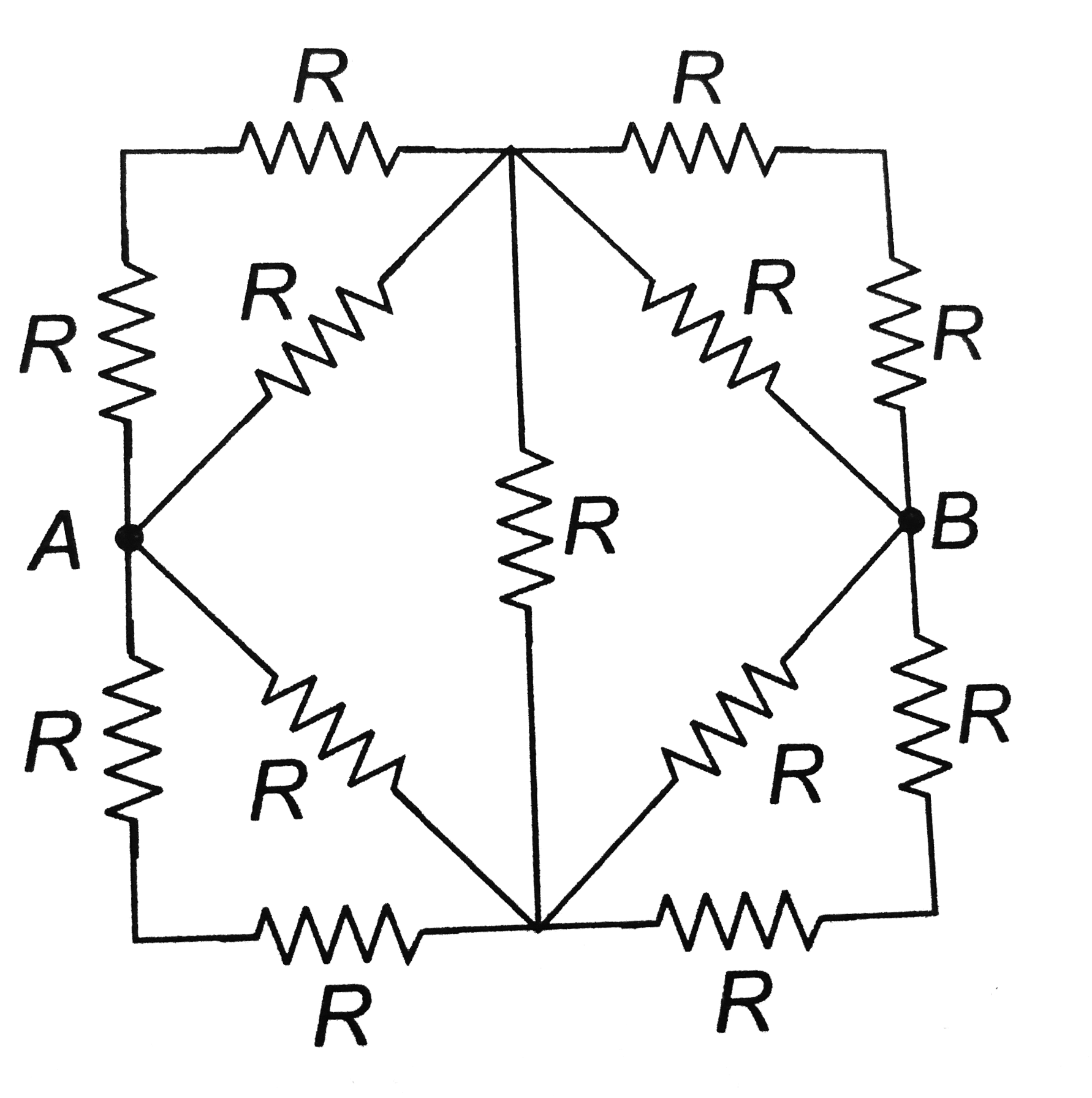
View SolutionThirteen resistances each of resistance R ohm are connected in the circuit as shown in the figure below. The effective resistance between A and B is

View SolutionThirteen resistances each of resistance R ohm are connected in the circuit as shown in the figure below. The effective resistance between A and B is

View SolutionA voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find the ratio of R1 and R2.
View Solution
